2447
Inferring Diffusion Tensors on Unregistered Cardiac DWI Using a Residual CNN and Implicitly Modelled Data Prior1Institute for Biomedical Engineering, University and ETH Zurich, Zürich, Switzerland
Synopsis
Cardiac DTI provides invaluable information about the state of myocardial microstructure. Motion and systematic signal variations of the imaging process influence the tensor inference. Image registration prior to tensor fitting with an LSQ estimator is the common data processing approach. The feasibility of training a neural network with simulated data modelling tensors and slice misalignment due to free breathing for inference of diffusion tensors from free-breathing in vivo data is investigated. Evaluation on simulated test data demonstrates feasibility of the training process. Application to in vivo data shows promising results of the CNN especially at myocardial borders.
Introduction
Cardiac diffusion tensor imaging (cDTI) has shown to provide invaluable information about the state of the myocardial microstructure in both healthy and diseased conditions1-5. Although it is a promising technique, challenges with respect to motion sensitivity remain to be addressed. Cardiac motion-induced signal loss during data acquisition in spin-echo sequences can be alleviated by using second order motion-compensated diffusion gradient waveforms6-8. Patient-friendly free-breathing acquisition strategies often result in spatial misalignment of the data, which require the use of non-rigid registration prior to parameter inference. Since image contrast varies between diffusion-weighted images (DWI), registration can be challenging. To address this, the utilization of neural networks (NN) for registering DWIs is actively investigated9-11. NNs have also been proposed for DTI parameter estimation on registered data to address the ill-posed nature of such inverse problems12,13. Besides the noise sensitivity, systematic signal variation due to residual spatial mismatch combined with partial volume effects could cause instability in parameter inference. As this predominantly affects the border regions of the left ventricle (LV), a manually drawn LV mask usually excludes these areas1,5. Instead of reducing the spatial mismatch prior to parameter inference by image registration, thereby risking spatial averaging effects, the varying position can be interpreted as an additional probing dimension. To exploit this information, this work examines the feasibility of a convolutional neural network (CNN) based end-to-end parameter inference on SE-M012 data without an explicit registration step.Methods
A residual CNN (Fig. 1) was trained on simulated artificial data to infer the tensor-values from data according to the 2-shell b-value scheme used by von Deuster et al.14 Data was generated such that prior knowledge on physiological mean diffusivity (MD) and fractional anisotropy (FA) values obtained with M012 spin-echo cDTI is implicitly captured15. Additionally, non-rigid motion between diffusion weightings, obtained from in vivo data registration was incorporated into simulation. All modules for data-generation as well as network training and statistical analysis were implemented in Python 3.6.9 using TensorFlow 2.2.1, NumPy 1.18, SciPy 1.4.1.Data generation
- Rejection sample eigenvalue triples within such that MD and FA are uniformly distributed over the defined intervals.
- Generate tensor maps that represent a transmurally varying helix-angle (HA) and random patches of absolute E2 sheetlet angle (E2A) inside an in vivo LV mask.
- Randomly select a subset of reference points inside the LV mask and scale the selected tensors with the sampled eigenvalue triples from step 1.
- Interpolate the reference tensors in log-Euclidean space16 with a radial basis function kernel and a circular distance measure to obtain locally smooth tensor maps.
- Randomly generate a lesion inside the LV, repeat steps 1 to 4 with suitable parameters and combine the maps.
- Evaluate the imaging forward model of
the single-shot M012-SE-EPI sequence including multiple
coils and motion between each acquisition and introduce diffusion contrast by
evaluating the bilinear form according to $$$S(b_i)=S_0e^{-b_iD_{ij}b_j}$$$ with
$$$\langle b_i,b_i\rangle=b$$$.
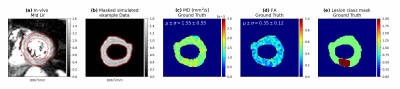
1500 diffusion datasets including 12 b-vectors ($$$b_i$$$ ) and 12 averages per diffusion weighting were simulated using 129 LV masks. As diffusion tensor ground truth for training, the simulation was performed without motion and noise addition followed by inference as linear least squares problem (LLSQ) with a Trust Region Reflective algorithm. Figure 2 illustrates a simulated example dataset. As loss function, the sum of mean squared errors (MSE) of the inferred tensor entries , MD and FA was used. To evaluate the performance of the network the mean absolute error (MAE) for MD, FA and eigenvalues of the tensors inferred on a simulated test dataset with unused LV-masks were calculated. As lower bound and upper bound of error the LLSQ inferences on noisy but perfectly aligned data and noisy unregistered data were evaluated. As no ground truth for in vivo data was available, a qualitative inspection of the network inference on data acquired in a previous study was performed.
Results
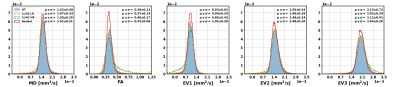
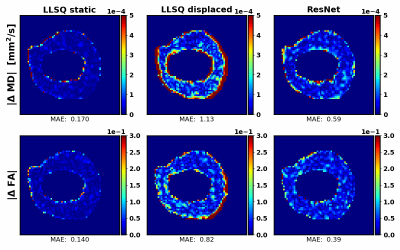
The distributions of inferred tensor metrics according to the described estimation for lower bound (LB), upper bound (UB) and the trained CNN compared to the simulated ground truth are shown in Fig 3. The normalized histogram show, that the CNN overall infers less outliers. Figure 4 shows absolute error maps of MD and FA for a subset of simulated test examples. The animated maps show outlier-errors at the border of the mask even for the LB estimation, which results from the mask being larger than the extend of the simulated LV. Therefore, an outlier rejection of absolute errors being 20 times larger than the median (resulting of ~2% of rejected values) is applied.This yields MAEs for MD and FA of tensors inferred on the simulated test data of $$$(|\Delta MD|_{LB}:2.2\cdot10^{-5} \frac{mm^2}{s}, |\Delta FA|_{LB}:1.8\cdot10^{-2})$$$ for the LB estimation, $$$(|\Delta MD|_{UB}:18\cdot10^{-5} \frac{mm^2}{s}, |\Delta FA|_{UB}:10\cdot10^{-2})$$$ for the UB estimation and $$$(|\Delta MD|_{ResNet}:8\cdot10^{-5} \frac{mm^2}{s}, |\Delta FA|_{ResNet}:5\cdot10^{-2})$$$ for the CNN.
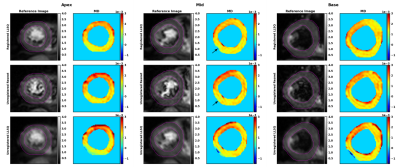
Figure 5 shows the MD values of inferred tensors for one in-vivo dataset.
Discussion
The results demonstrate the feasibility of training a CNN on simulated data to increase robustness of tensor inference for cDTI by implicitly including systematic and random signal variations as a data prior. While the inference on in vivo data shows promising results, further evaluation on data including lesions is necessary.Acknowledgements
Swiss National Science Foundation Grant PZ00P2_174144
References
1. Nielles-Vallespin S, Scott A, Ferreira P, Khalique Z, Pennell D, Firmin D. Cardiac Diffusion: Technique and Practical Applications. J Magn Reson Imaging. Published online 2019. doi:10.1002/jmri.26912
2. Gotschy A, von Deuster C, van Gorkum RJH, et al. Characterizing cardiac involvement in amyloidosis using cardiovascular magnetic resonance diffusion tensor imaging. J Cardiovasc Magn Reson. 2019;21(1):56. doi:10.1186/s12968-019-0563-2
3. von Deuster C, Sammut E, Asner L, et al. Studying Dynamic Myofiber Aggregate Reorientation in Dilated Cardiomyopathy Using In Vivo Magnetic Resonance Diffusion Tensor Imaging. Circ Cardiovasc Imaging. 2016;9(10). doi:10.1161/CIRCIMAGING.116.005018
4. Zohya K, F. FP, D. SA, et al. Diffusion Tensor Cardiovascular Magnetic Resonance in Cardiac Amyloidosis. Circ Cardiovasc Imaging. 2020;13(5):e009901. doi:10.1161/CIRCIMAGING.119.009901 5. Das A, Chowdhary A, Kelly C, et al. Insight Into Myocardial Microstructure of Athletes and Hypertrophic Cardiomyopathy Patients Using Diffusion Tensor Imaging. J Magn Reson Imaging. 2021;53(1):73-82. doi:https://doi.org/10.1002/jmri.27257
6. Stoeck CT, von Deuster C, Genet M, Atkinson D, Kozerke S. Second-order motion-compensated spin echo diffusion tensor imaging of the human heart. Magn Reson Med. 2016;75(4):1669-1676. doi:10.1002/mrm.25784
7. Welsh CL, Dibella EVR, Hsu EW. Higher-Order Motion-Compensation for In Vivo Cardiac Diffusion Tensor Imaging in Rats. 2015;34(9):1843-1853. doi:10.1109/tmi.2015.2411571
8. Lasic S, Szczepankiewicz F, Dall’Armellina E, et al. Motion-compensated b-tensor encoding for in vivo cardiac diffusion-weighted imaging. NMR Biomed. 2020;33(2):e4213. doi:10.1002/nbm.4213
9. Ferreira PF, Martin RR, Scott AD, et al. Automating in vivo cardiac diffusion tensor postprocessing with deep learning–based segmentation. Magn Reson Med. 2020;84(5):2801-2814. doi:10.1002/mrm.28294
10. Deng Z, Wang L, Wu Q, et al. Investigation of in Vivo Human Cardiac Diffusion Tensor Imaging Using Unsupervised Dense Encoder-Fusion-Decoder Network. IEEE Access. Published online 2020:1. doi:10.1109/ACCESS.2020.3040330
11. Nguyen CT, Christodoulou AG, Coll-Font J, et al. Free-breathing diffusion tensor MRI of the whole left ventricle using second-order motion compensation and multitasking respiratory motion correction. Magn Reson Med. 2020;n/a(n/a). doi:https://doi.org/10.1002/mrm.28611
12. Aliotta E, Nourzadeh H, Sanders J, Muller D, Ennis DB. Highly accelerated, model-free diffusion tensor MRI reconstruction using neural networks. Med Phys. 2019;46(4):1581-1591. doi:10.1002/mp.13400
13. Aliotta E, Nourzadeh H, Patel SH. Extracting diffusion tensor fractional anisotropy and mean diffusivity from 3-direction DWI scans using deep learning. Magn Reson Med. 2021;85(2):845-854. doi:https://doi.org/10.1002/mrm.28470
14. von Deuster C, Stoeck CT, Genet M, Atkinson D, Kozerke S. Spin echo versus stimulated echo diffusion tensor imaging of the in vivo human heart. Magn Reson Med. 2016;76(3):862-872. doi:https://doi.org/10.1002/mrm.25998
15. Das A, Kelly C, Teh I, Stoeck CT, Kozerke S, Brown LAE, Saunderson CED, Craven T, Swoboda PP, Levelt E, Greenwood JP, Plein S, Schneider JE, Dallarmellina. Longitudinal changes in diffusion tensor imaging parameters following acute ST elevation myocardial infarction. Proceedings of the 17th Annual Meeting of the European Association of Cardiovascular Imaging. 2019; P459.
16. Arsigny V, Fillard P, Pennec X, Ayache N. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magn Reson Med. 2006;56(2):411-421. doi:10.1002/mrm.20965
Figures

Figure 1: Architecture design of the proposed residual CNN. Input is 144 stacked diffusion-weighted magnitude images, normalized to the mean LV intensity of the first image. The final output 6 channels represents the tensor entries. Convolutional layers (blue) have a $$$3\times3\times N$$$ kernel and ReLU activation. The residual blocks (green) consist of the parallel paths with different kernel sizes. The outputs are concatenated and reduced 1 convolution layer to match the input channels. The output of a residual block is added to the skip connection and fed to the next block.