2446
SRDTI: Deep learning-based super-resolution for diffusion tensor MRI1Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States, 2Harvard Medical School, Boston, MA, United States, 3Department of Biomedical Engineering, Tsinghua University, Beijing, China, 4Department of Electrical Engineering, Stanford University, Stanford, CA, United States
Synopsis
High-resolution diffusion tensor imaging (DTI) is beneficial for probing tissue microstructure in fine neuroanatomical structures, but long scan times and limited signal-to-noise ratio pose significant barriers to acquiring DTI at sub-millimeter resolution. To address this challenge, we propose a deep learning-based super-resolution method entitled “SRDTI” to synthesize high-resolution diffusion-weighted images (DWIs) from low-resolution DWIs. SRDTI employs a deep convolutional neural network (CNN), residual learning and multi-contrast imaging, and generates high-quality results with rich textural details and microstructural information, which are more similar to high-resolution ground truth than those from trilinear and cubic spline interpolation.
Introduction
Diffusion tensor imaging (DTI) is widely used for mapping major white matter tracts and probing tissue microstructure in the brain1,2. High-resolution DTI (e.g., 1.25 mm isotropic adopted by the Human Connectome Project (HCP) WU-Minn-Oxford Consortium3) is beneficial for probing tissue microstructure in fine neuroanatomical structures, such as cortical anisotropy and fiber orientations4. However, long scan times and limited signal-to-noise ratio (SNR) pose significant barriers to acquiring DTI at high resolution in routine clinical and research applications, especially at millimeter and sub-millimeter isotropic resolution. Standard 2D acquisitions with single-shot EPI readout suffers from extremely high image blurring and distortion and low SNR, while slab acquisitions5-7 and multi-shot EPI8-10 are not widely available due to the requirement of advanced sequences and reconstruction methods.Super-resolution imaging provides a viable way to achieve DTI at higher resolution in the spirit of image quality transfer11. Previous studies have demonstrated the feasibility of deep learning in super-resolution DTI12. We propose a deep learning method entitled “SRDTI” to synthesize high-resolution diffusion-weighted images (DWIs) from low-resolution DWIs. Unlike previous studies using a shallow convolutional neural network (CNN), SRDTI employed a very deep 3D CNN, residual learning and multi-contrast information sharing. We compared our results to those from image interpolation and quantified the improvement in terms of both image and DTI metrics quality.
Methods
Data. Pre-processed T1-weighted (0.7-mm isotropic) and diffusion data (1.25-mm isotropic, b=1,000 s/mm2, 90 uniform directions) of 200 healthy subjects (144 for training, 36 for validation, 20 for evaluation) from the HCP WU-Minn-Oxford Consortium were used13. Low-resolution data were simulated by down-sampling the high-resolution data to 2 mm iso. resolution using sinc interpolation. Co-registered T1-weighted data were resampled to 1.25-mm isotropic resolution.Network Implementation. SRDTI utilizes a very deep 3D CNN14-16 (10 layers, 192 kernels per layer) to learn the mapping from the input low-resolution image volumes to the residuals between the input and output high-resolution image volumes (residual learning) (Fig. 1). The inputs of SRDTI are low-resolution b=0 image volume and six DWI volumes up-sampled to 1.25-mm isotropic resolution, and a T1-weighted volume. The outputs of SRDTI are ground-truth high-resolution b=0 image volume and six DWI volumes. The b=0 image volumes were obtained by averaging all b=0 image volumes. The DWI volumes were synthesized from the fitted diffusion tensor along six optimized diffusion-encoding directions, which minimize the condition number of the diffusion tensor transformation matrix17, and were therefore equivalent to the six diffusion tensor components in the image space. Operating in the image space rather than the tensor component space improved data similarity in local regions and avoids unreliable tensor fitting in cerebrospinal fluid voxels. Anatomical images are often acquired along with diffusion data and were therefore included as an additional channel to outline different tissues and preserve structural detail in the output DWIs. SRDTI was implemented using the Keras API (https://keras.io/) with a Tensorflow (https://www.tensorflow.org/) backend. Training was performed with 64×64×64 voxel blocks, Adam optimizer, L2 loss using an NVidia V100 GPU.
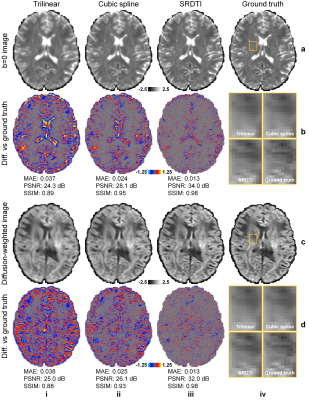
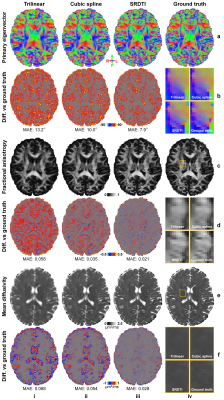
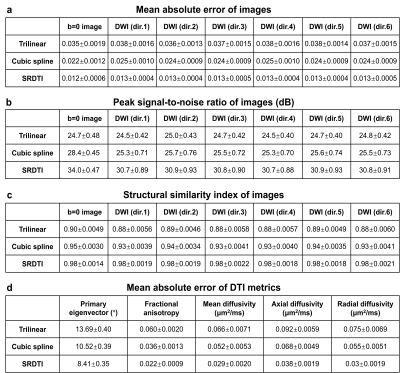
Evaluation. For comparison, low-resolution diffusion data were also up-sampled to 1.25-mm isotropic using trilinear and cubic spline interpolation. The mean absolute error (MAE), peak SNR (PSNR) and structural similarity index (SSIM) were used to quantify image similarity comparing to ground-truth high-resolution images. The MAE of DTI metrics, including primary eigenvector (V1), fractional anisotropy (FA), mean, axial, and radial diffusivities (MD, AD, RD) and comparing to ground-truth high-resolution results were also calculated and compared.
Results
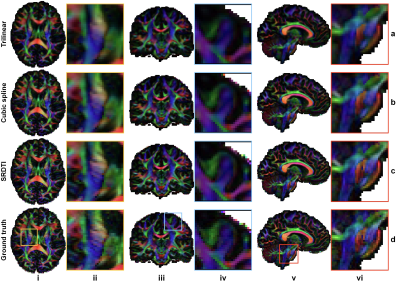
The b=0 image and DWIs at 1.25 mm isotropic resolution generated by SRDTI recovered more textural details and were visually similar to the ground-truth images (Fig. 2). The images were also quantitatively similar to the ground-truth images (Figure 5a-c), with low MAEs around 0.012, high PSNRs around 31 dB and high SSIM around 0.98. The residuals between the super-resolved images and ground-truth high-resolution images did not contain anatomical structure (Fig. 2b,d).The V1-encoded FA maps from SRDTI displayed captured the striated appearance of the gray matter bridges spanning the internal capsule in the striatum (Fig. 3i), as well as known cortical anisotropy (Fig. 3ii) and the fine fiber pathways in the pons (Fig. 3iii). Quantitatively, the MAEs of the output DTI metrics were also low, with MAEs of 8.41°±0.35° for V1, 0.022±0.0009 for FA, and 0.029±0.002 μm2/ms, 0.038±0.0019 μm2/ms and 0.03±0.0019 μm2/ms for MD, AD and RD, which were 35% to 80% of the MAE’s calculated for the corresponding DTI metrics obtained from trilinear and cubic spline interpolated images (Figure 5d).
Discussion and Conclusion
We obtained high-quality super-resolution DWIs and DTI metrics at 1.25 mm isotropic resolution from low-resolution DWIs at 2 mm isotropic resolution (~4.1× voxel volume difference) using SRDTI, which employs a very deep 3D CNN and residual learning. Our results recover detailed microstructural information and demonstrate substantial improvement over the results derived from trilinear and cubic spline interpolation. SRDTI can be generalized to high-b-value data for mapping crossing fibers and more advanced microstructural models (e.g., diffusion kurtosis imaging and NODDI18). SRDTI can also be used to super-resolve sub-millimeter isotropic resolution images obtained from slab acquisitions and multi-shot EPI as well as lower-resolution images acquired using standard 2D sequences with single-shot EPI. Future work will compare SRDTI to other super-resolution methods.Acknowledgements
This work was supported by the NIH (grants P41-EB030006, U01-EB026996, R21-AG067562, K23-NS096056) and an MGH Claflin Distinguished Scholar Award.References
1. Basser, P. J., Mattiello, J. & LeBihan, D. MR diffusion tensor spectroscopy and imaging. Biophysical journal 66, 259-267 (1994).
2. Pierpaoli, C., Jezzard, P., Basser, P. J., Barnett, A. & Di Chiro, G. Diffusion tensor MR imaging of the human brain. Radiology 201, 637-648 (1996).
3. Sotiropoulos, S. N. et al. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. NeuroImage 80, 125-143 (2013).
4. McNab, J. A. et al. Surface based analysis of diffusion orientation for identifying architectonic domains in the in vivo human cortex. NeuroImage 69, 87-100 (2013).
5. Wu, W., Koopmans, P. J., Andersson, J. L. & Miller, K. L. Diffusion Acceleration with Gaussian process Estimated Reconstruction (DAGER). Magnetic resonance in medicine 82, 107-125 (2019).
6. Setsompop, K. et al. High‐resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (g S lider‐SMS). Magnetic resonance in medicine 79, 141-151 (2018).
7. Liao, C. et al. High-fidelity, high-isotropic-resolution diffusion imaging through gSlider acquisition with and T1 corrections and integrated ΔB0/Rx shim array. Magnetic Resonance in Medicine 83, 56-67 (2020).
8. Bilgic, B. et al. Highly accelerated multishot echo planar imaging through synergistic machine learning and joint reconstruction. Magnetic Resonance in Medicine 82, 1343-1358, doi:10.1002/mrm.27813 (2019).
9. Hu, Y. et al. Motion‐robust reconstruction of multishot diffusion‐weighted images without phase estimation through locally low‐rank regularization. Magnetic resonance in medicine 81, 1181-1190 (2019).
10. Hu, Y. et al. Multi-shot diffusion-weighted MRI reconstruction with magnitude-based spatial-angular locally low-rank regularization (SPA-LLR). Magnetic Resonance in Medicine 83, 1596-1607 (2020).
11. Alexander, D. C. et al. Image quality transfer and applications in diffusion MRI. NeuroImage 152, 283-298 (2017).
12. Elsaid, N. M. & Wu, Y.-C. in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). 2830-2834 (IEEE).
13. Glasser, M. F. et al. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage 80, 105-124 (2013).
14. Zhang, K., Zuo, W., Chen, Y., Meng, D. & Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Transactions on Image Processing 26, 3142-3155 (2017).
15. Kim, J., Kwon Lee, J. & Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 1646-1654 (2016).
16. Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. Preprint at: https://arxiv.org/abs/1409.1556 (2014).
17. Skare, S., Hedehus, M., Moseley, M. E. & Li, T.-Q. Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. Journal of Magnetic Resonance 147, 340-352 (2000).
18. Zhang, H., Schneider, T., Wheeler-Kingshott, C. A. & Alexander, D. C. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage 61, 1000-1016 (2012).
Figures