Introduction

Multi-shell diffusion MRI has informed our understanding of the brain, both at the level of local microstructure as well as distributed long-range network properties. Multiple b-values are used to study the angular properties of the diffusion signal, in particular the directionality of fiber bundles in white matter (WM). Typically, these high b-values result in lower signal-to-noise ratios (SNR), which can be compensated for by higher sampling (averaging) and longer scan times which are prohibitive in clinical scenarios. To compensate for low SNR, various signal denoising techniques have been proposed including low-rank approximations¹, compressed sensing² and model-based denoising methods³. Current unsupervised model-free denoising methods require a noise model to do the denoising, either as an explicit standard deviation and covariance, or implicitly in the choice of a noise correction method. Here we propose an unsupervised, model-free deep learning based denoising method that operates on the MR k-space raw data, eliminating the requirement to select or calibrate a noise model.

Methods

Data from four acquisitions from two healthy volunteers were acquired under IRB-approval, on a whole-body 3T system (GE SIGNA MR750), equipped a high-performance head-gradient coil MAGNUS^4,5, and using a 32-channel phased array head coil (NOVA Medical, Wilmington, MA). The MAGNUS gradient coil was operates at 200 mT/m with a maximum slew rate of 500 T/m/s for the diffusion gradients⁵. Multi-shell acquisitions were performed with either 300 (N=3 acquisitions) or 150 (N=1 acquisition) directions uniformly sampled over a sphere at b-values of 500, 1000, 2000, and 4000 s/mm2. Volunteer 1 was scanned twice with 300-direction diffusion acquisition and volunteer 2 was scanned twice with 300 and 150-direction diffusion acquisition. An additional 16 non-diffusion-weighted images (i.e., b=0) were interspersed through the acquisition. For a TR/TE = 44.2/7000 ms, 160x160 matrix, 86 slices, the 300 or 150-direction diffusion data were acquired with an isotropic resolution of 1.5x1.5x1.5 mm³. Diffusion images were denoised using commercially-available GE “AIR^TM Recon DL” deep learning network⁶. Deep learning based denoising was performed at various intensities (50% and 75%) for comparison. The acquisition of the 300-direction data set allowed sub-sampling of the diffusion q-space to reduce the number of directions and provide the ability to characterize the denoising improvement compared to the longer scan with the large number of directions. All images (with or without DL based denoising) were post-processed using a custom -built pipeline. After distortion correction (rigid motion and eddy currents) using affine registration, standard diffusion tensor imaging parameters (fractional anisotropy (FA)) as well as diffusion kurtosis imaging parameters (parallel kurtosis (KPar), orthogonal kurtosis (KOrth)) were computed from the diffusion-weighted images. For WM parcellation, the individual subject images were non-rigidly registered to the FA atlas (John Hopkin’s ICBM DTI-81) with 50 parcellated WM regions, and the mean and standard deviation of all the diffusion maps within each of the parcels was computed.

Results

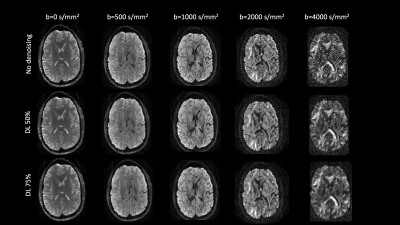
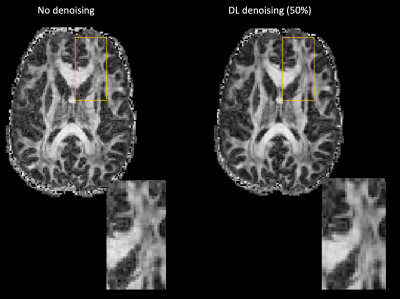
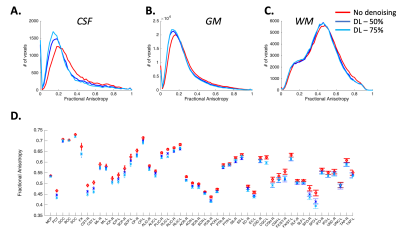
Qualitative assessment demonstrates superior performance of DL based denoising without compromising structural acuity especially at high b-values (Figure 1). Fractional anisotropy maps showed improved differentiation of signal components while reducing artifacts (Figure 2). Distribution of FA values across WM, Gray matter (GM) and CSF was computed (Figure 3A-C) to quantitatively assess the effect of DL-based denoising on the different signal compartments. While the distribution FA values in the whole-body WM was preserved, FA values in the DL-based denoised data were significantly lower than non-denoised images (Figure 3A) indicating a reduction of overall noise. Looking more closely, FA values in the individual WM parcels (50 WM parcels derived from the JHU-atlas) were preserved even after denoising, indicating that DL-based denoising did not alter or smooth quantitative diffusion maps. Tensor-derived diffusion metrics were compared between reference 300-direction and 150-direction diffusion data (volunteer 2) with and without DL denoising. While FA and KPar were not significantly different in the 150-direction compared to reference 300-direction data, KOrth values computed from DL denoised data were closer to reference values compared to non-denoised data.

Conclusion and Discussion

Here we demonstrate initial results from a model-free DL-based denoising of diffusion weighted images and show reduced noise and improved Gray matter, White matter and CSF differentiation, without compromising quantitative diffusion metrics in individual WM regions. This DL-based approach does not require selection of a specific noise model and can potentially be used to accelerate acquisitions with minimal loss in quantitative diffusion metrics and robust structural connectivity.

Acknowledgements

Grant funding from NIH U01EB28976, NIH U01EB024450, and CDMRP W81XWH-16-2-0054