Introduction

The balanced SSFP frequency response comprises rich information about the intravoxel frequency content¹. Pronounced bSSFP profile asymmetries observed in white matter (WM) have revealed a strong sensitivity to the fiber tract orientation relative to B₀ and a significant correlation with diffusion metrics such as fractional anisotropy (FA) or tract directionality measures reflected by the principal diffusion eigenvector (V1) has been reported². Driven by recent work, which demonstrated that neural networks (NNs) can predict relaxation times and field map estimates from the bSSFP profile³, we explore if additionally multiple diffusion parameters obtained by diffusion tensor imaging (DTI) can be learned. DTI imaging is sensitive to microstructural diffusion processes of water molecules allowing the detection of anisotropies in the tissue microenvironment and the delineation of WM fiber pathways^4,5. Here, besides mean diffusivity (MD) and FA, the two spherical angles (azimuth Φ, inclination ϴ) characterizing the major diffusion eigenvector are chosen as targets for the NN training.

Methods

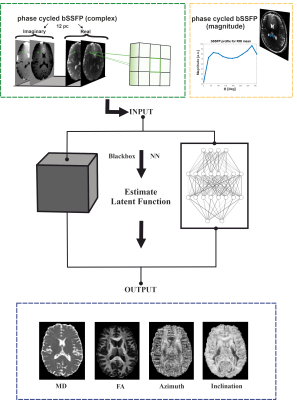
Five healthy volunteers were measured at 3T (Prisma, Siemens Healthineers); the data of one was used for NN testing while the data of the other four were used to train feedforward NNs with in total ~630.000 training voxels. NN input data was obtained from whole-brain 3D sagittal bSSFP scans with 12 uniformly distributed phase-cycles in the range (0°, 360°), i.e., φ_j = 180/12∙(2j-1), j = 1,2,…12, at an isotropic resolution of 1.3x1.3x1.3 mm³ with 128 partitions, a TR/TE of 4.8 ms/2.4 ms, α_nom = 15°, and 256 dummy preparation pulses before each phase-cycle acquisition. Using GRAPPA acceleration 2, the total scan time was 10 min 12 s. NN ground-truth data were acquired using a standard axial 2D multi-slice spin-echo echo-planar imaging (SE-EPI) DTI sequence. Diffusion-sensitized scans were performed with a bipolar diffusion gradient scheme along 20 directions for a b-value of 1000 s/mm². Additionally, a single non-diffusion weighted (b-value=0) dataset was acquired. Protocol parameters included a resolution of 1.4x1.4x3.0 mm³, 36 slices for whole-brain coverage, a TR/TR of 4800 ms/83 ms, GRAPPA acceleration 2, 9 averages per direction and b-value, yielding a total acquisition time of 15 min 23 s. To correct susceptibility- and eddy current-induced distortions, the non-diffusion weighted scan was repeated with opposite phase encoding direction. DTI fitting of the distortion-corrected data resulted in the desired MD, FA, and V1 outputs. The principal eigenvector V1 was transformed from Cartesian (x,y,z) to spherical (r, Φ, ϴ) coordinates (r=1 per definition). The inclination ϴ corresponds to the angle between V1 and B₀. The four diffusion metrics MD, FA, Φ, ϴ served as targets for the NN. Voxels classified as WM or GM were included into the NN training. NN models were implemented using the open-source Python library Keras. As sketched in Figure 1, a 3x3 window of nearest neighbors was defined for each voxel in the axial plane to support the NN with additional spatial input information. Stacking real and imaginary parts of the acquired 12-point complex bSSFP profile for a 3x3 window resulted in 216 input features. Embedding the maximum likelihood principle in the loss function of the NN training process allowed the voxelwise determination of uncertainties for each target parameter during training^6,7. Bayesian hyperparameter optimization with Gaussian processes was used to find optimal NN models. The optimization took ~13h and suggested an architecture of 4 hidden layers, 191 neurons, and a batch size of 32.

Results

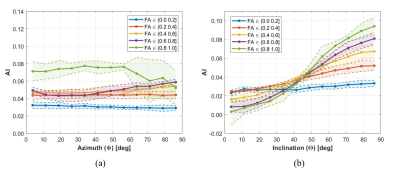
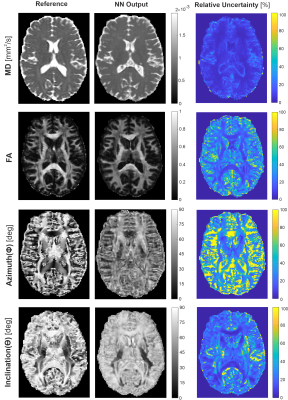
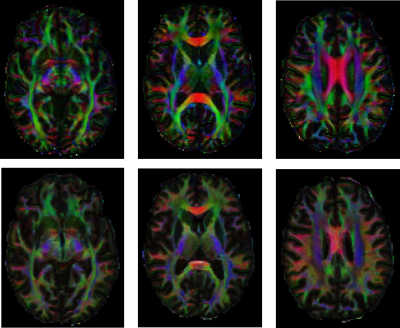
As evident from Figure 2b, bSSFP profile asymmetries in WM strongly depend on the inclination ϴ, which is equivalent to the angle between the fiber tract directionality (≡ V1) and B₀. The asymmetry index (AI) increases clearly, when incrementing ϴ from parallel (0°) to orthogonal (90°) tract orientation relative to B₀, with steeper slopes the higher the FA. On the other hand, the AI values are almost unaffected by the azimuthal angle Φ, however, at higher levels with increasing FA (Fig. 2a). Figure 3 displays DTI reference data and NN predictions of MD, FA, Φ, and ϴ for an exemplary axial slice from an unseen testing subject, as well as the relative NN uncertainty maps. Low uncertainties are achieved for MD, FA, and ϴ, in particular in WM as expected. Distinct bSSFP profile asymmetries in WM represent valuable information for NN FA and ϴ estimation (cf. Fig. 2b) while the azimuthal angle Φ is less correlated (cf. Fig. 2a), which results in higher uncertainties. The potential of the NN predicted diffusion metrics to delineate WM fiber tract orientations is investigated in Figure 4 by the calculation of color-coded fiber direction maps (V1 obtained from (Φ, ϴ) weighted by FA). The loss in brightness and structure of the predicted maps in comparison to the reference is mainly explained by a slight underestimation in FA and structural deficiencies in the azimuthal angle maps.

Discussion and Conclusion

Feedforward NNs revealed strong potential for robust NN prediction of MD, FA, and ϴ with low uncertainties especially in WM structures. The quality of NN predicted color-coded fiber direction maps was yet degraded due to low NN performance in the predicted Φ maps, which may be improved in future studies using image-based learning approaches with convolutional neural networks.

Acknowledgements

No acknowledgement found.