Introduction

Multimodal brain imaging has become increasingly popular for both research and clinical applications.¹ These multimodal images provide complementary information of brain tissues which, if used properly, can provide a more comprehensive understanding of brain function and disorders.^2-4 However, due to the high dimensionality of multimodal image data, it is challenging to capture the underlying joint spatial and cross-modal dependence required for statistical inference in various brain image processing tasks. Conventional methods usually process each modality individually and then combine the results in the final stage,⁵ although efforts have been made to capture pairwise dependence between different modalities.^6,7 Recently, deep learning-based methods have shown the potential to capture higher-order statistical dependence among multiple modalities.^8,9 But those networks often require huge amounts of training data to avoid the over-fitting problem, which are often beyond what are currently available in various brain imaging applications. In this study, we proposed a new multimodal image fusion method, which synergistically integrates tensor modeling with deep learning. The tensor model was used to capture the joint spatial-intensity-modality dependence and deep learning was used to fuse intensity and spatial-intensity-modality information. While the proposed method is useful for a range of multimodal brain image processing tasks, including disease detection, classification and prediction, in this work, we focused on multimodal brain image segmentation to demonstrate its feasibility and potential.

Method

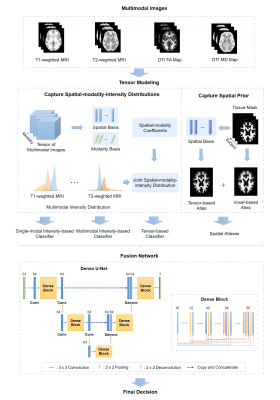
A fundamental problem in multimodal image fusion is to estimate the underlying joint probability distributions. This problem is challenging due to the difficulty associated with estimating high-dimensional probability functions and limited training data available. A common approach is to perform dimension reduction and/or assume some level of statistical independence of the multimodal data.¹⁰ In this work, a tensor model was used for dimension reduction and to capture the joint spatial-intensity-modality dependence.

Tensor model as a dimension reduction transform
It is well known that a high-dimensional function, $$$I(x_1,x_2,…,x_d)$$$ can be well approximated by lower dimensional functions as ¹¹:$$I(x_1,x_2,…,x_d)≈\sum_{l_1=1}^{L_1}\sum_{l_2=1}^{L_2}…\sum_{l_{\hat{d}}=1}^{L_{\hat{d}}}c_{l_1,l_2,…,l_{\hat{d}}}g_{l_1}^{{1}}({\bf{x}}_1)g_{l_2}^{{2}}{({\bf{x}}_2)}…g_{l_{\hat{d}}}^{{\hat{d}}}{({\bf{x}}_{\hat{d}})}\hspace{5cm}[1]$$where $$$\{{{\bf{x}}_1,{\bf{x}}_2,…{\bf{x}}_d ̂ }\}$$$ represents $$${\hat{d}}$$$ groups of “separable” variables from $$$\{{x_1,x_2,…,x_d}\}$$$. In our problem, we have $$$d={\hat{d}},\,x_1=x,\,x_2=y,\,x_3=z$$$, and $$$x_4=m$$$ that represents different modalities. Eq. [1] can be further expressed in a tensor form as:$$\mathcal{P}≈\mathcal{C}×_1G^{(1)}×_2G^{(2)}×…×_{\hat{d}}G^{({\hat{d}})}\hspace{5cm}[2]$$where $$$\mathcal{P}\in\mathbb{C}^{N_1×N_2×…×N_{\hat{d}}}$$$, $$$G^{(j)}∈\mathbb{C}^{N_j×L_j}$$$ and $$$\mathcal{C}\in\mathbb{C}^{L_1×L_2×…×L_{\hat{d}}}$$$ is the core tensor. We used the tensor model for two tasks: a) efficient representation of joint spatial-modality-intensity distributions; and b) dimension reduction of prior spatial probability distributions.

Task 1 includes three components: 1) determination of the tensor spatial-modality subspace; 2) estimation of the coefficients associated with the estimated subspace; and 3) joint intensity-spatial-modality distribution estimation. For the first problem, we applied high-order SVD to the training data to estimate the spatial-modality subspace as $$$\{{{\hat{G}}^{(i)}\}}_{i=1}^{{\hat{d}}-1}$$$. After that, the coefficients $$$w$$$ were obtained by projecting the multimodal data to the principal subspace such that $$${\hat{w}}={\hat{G}}^{({\hat{d}})}{\hat{C}}_{({\hat{d}})}={\hat{P}}_{({\hat{d}})}{\hat{Φ}}^{T}$$$, where $$${\hat{Φ}}=({\hat{G}}^{({\hat{d}}-1)}⊗{\hat{G}}^{({\hat{d}}-2)}⊗…⊗{\hat{G}}^{(1)} )^{T}$$$, $$${\hat{P}}_{({\hat{d}})}$$$ is the mode-$$${\hat{d}}$$$ matricization of $$$\mathcal{P}$$$, $$${\hat{C}}_{({\hat{d}})}$$$ is the mode-$$${\hat{d}}$$$ matricization of $$$\mathcal{C}$$$, and $$$⊗$$$ denotes the Kronecker product. Finally, the joint intensity-spatial-modality distribution was represented by the joint intensity and spatial-modality coefficients distribution using a mixture of Gaussians (MoG) model and the parameters could be estimated under the maximum likelihood principle.

For task 2, the prior spatial probability map of each brain tissue was generated from training data and was formed as a second-order tensor $$$\mathcal{T}\in\mathbb{C}^{N_1×N_2}$$$, which can be decomposed as: $$\begin{equation}\mathcal{T}≈\mathcal{S}×_1U^{(1)}×_2U^{(2)}\end{equation}\hspace{5cm}[3]$$ where $$$U^{(j)}∈\mathbb{C}^{N_j×L_j}$$$ represents the spatial/population basis of the model. The multimodal intensity distributions were projected to the estimated spatial-population subspace to get the tensor-based spatial statistical atlas The obtained joint spatial-modality-intensity distributions and spatial atlas were then integrated to build a tensor-based classifier.

Deep learning to fuse intensity and spatial-intensity-modality information
A Dense U-Net was used to integrate the following components: a) single-modal intensity-based classifiers; b) a multimodal intensity-based classifier; c) a tensor-based classifier; d) spatial atlases.¹² The pipeline of our proposed fusion framework is illustrated in Figure 1.

Results and Discussion

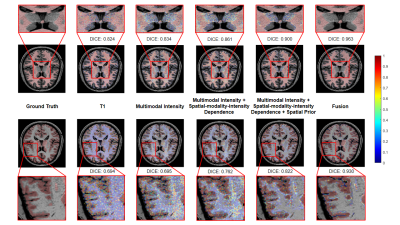
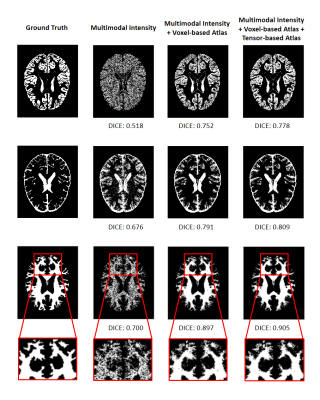
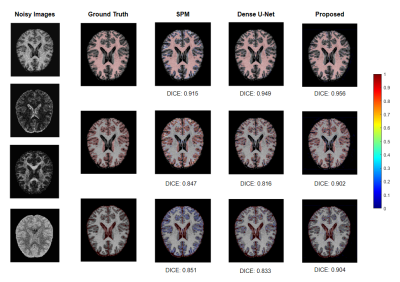
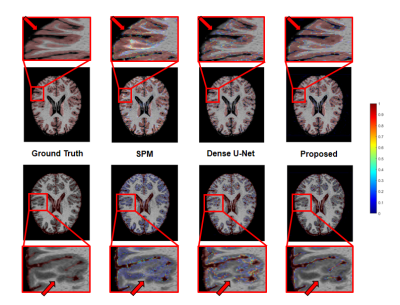
We applied our proposed fusion method to a multimodal brain tissue segmentation task and evaluate the performance using the Human Connectome Project (HCP) dataset.¹³ Gaussian noise was added to the original images to generate our testing data. Figure 2 shows a performance comparison by adding in each component in our fusion framework. The segmentation accuracy was improved with more features being added, which confirms the advantage of capturing spatial-intensity-modality dependence information. Figure 3 shows the advantage of combining the tensor-based spatial statistical atlas and the commonly used voxel-based spatial atlas. As can be seen, the segmentation performance was significantly improved after adding the tensor-based spatial atlas. Figure 4 compares the proposed method with other segmentation methods using SPM or Dense U-Net on noisy images.^12,14 The proposed method produced more accurate segmentation results than the others. Figure 5 shows the tissue details of the segmentation results. As can be seen, our method performed much better in segmenting the cerebrospinal fluid branches.

Conclusion

This paper presents a novel method for multimodal fusion, which synergistically integrates tensor modeling and deep learning. The proposed method was applied to multimodal brain image segmentation, producing significantly improved results over state-of-the-art methods. With further development, the proposed method can provide a powerful tool for many multimodal brain image processing tasks, including disease detection, classification and prediction.

Acknowledgements

Y. L. is funded by National Science Foundation of China (No.61671292 and 81871083) and Shanghai Jiao Tong University Scientific and Technological Innovation Funds (2019QYA12).