2413

Fully-Automated Deep Learning-Based Background Phase Error Correction for Abdominopelvic 4D Flow MRI
Sophie You1, Evan M. Masutani1, Joy Liau2, Marcus T. Alley3, Shreyas S. Vasanawala3, and Albert Hsiao2
1School of Medicine, University of California, San Diego, La Jolla, CA, United States, 2Department of Radiology, University of California, San Diego, La Jolla, CA, United States, 3Department of Radiology, Stanford University School of Medicine, Stanford, CA, United States

Synopsis

4D Flow MRI is valuable for the evaluation of cardiovascular disease, but abdominal applications are currently limited by the need for background phase error correction. We propose an automated deep learning-based method that utilizes a multichannel 3D convolutional neural network (CNN) to produce corrected velocity fields. Comparisons of arterial and venous flow, as well as flow before and after bifurcation of major abdominal vessels, show improved flow continuity with greater agreement after automated correction. Results of automated corrections are comparable to manual corrections. CNN-based corrections may improve reliability of flow measurements from 4D Flow MRI.

Introduction

Time-resolved 3D phase-contrast MRI with three-dimensional velocity encoding (4D Flow MRI) has become increasingly valuable for the evaluation of cardiovascular disease1. While cardiothoracic and neurovascular applications have grown rapidly2,3, a limiting factor for abdominal applications is the correction of magnetic eddy current-related background phase error4-6, which can be more challenging to reliably correct in abdominopelvic regions due to complex vascular and soft tissue geometry7. Phase-error correction is essential for both quantification of blood flow as well as for visualization (Figure 1). We propose a fully-automated approach to background phase-error correction that leverages deep learning to predict the velocity correction field, and hypothesize that this method may be used to replace current correction methods, which require manual identification of static soft tissue.

Methods

With IRB approval and HIPAA compliance, we retrospectively collected 26 abdominal 4D Flow MRI acquisitions performed at our institution as part of routine clinical MRI examinations. Examinations were completed on 3T 750 MRI (GE Healthcare, Milwaukee, Wisconsin) using a 32-channel phased-array coil. 4D Flow MRI was performed with a 3D cartesian strategy in which (Ky-Kz) samples were grouped in spiral-like sets and acquired with golden angle ordering8,9, evenly spaced over time10 with dense central k-space sampling for respiratory soft gating11. Encoding velocity ranged from 80 to 250 cm/s. Vessel segmentation and manual phase-error correction were performed using dedicated imaging software (Arterys, San Francisco, CA) and supervised by a board-certified radiologist with more than a decade of experience working with 4D Flow. Manual correction was performed via segmentation of static tissue followed by a patch-wise linear regression of static tissue velocities. After 30% of the data (8 patients) was reserved for testing, the remaining 70% (360 temporal volumes from 18 patients) was used to train a multichannel, 3D convolutional neural network (CNN). Architecture of the U-Net12, a type of CNN, is shown in Figure 2. CNN-predicted velocity corrections for the three velocity components were then reduced to third-order polynomial least-squares approximations, which were added to the uncorrected velocity arrays to generate polynomial-corrected velocities. The postprocessing pipeline is illustrated in Figure 3. Segmentation for flow quantification was performed for the infrarenal aorta in triplicate, and individually for the right and left common iliac arteries (LCIA, RCIA), inferior vena cava (IVC), and left and right common iliac veins (LCIV, RCIV). Internal consistency of flow measurements was established by assessing conservation of mass. The aorta was compared to the LCIA+RCIA, while the IVC was compared to the LCIV+RCIV. Each arterial vessel was compared to its venous counterpart (aorta vs. IVC, LCIA vs. LCIV, and RCIA vs. RCIV). Statistical comparisons between uncorrected, manually-corrected, and polynomial-corrected flow were assessed using Bartlett’s test of homogeneity of variances followed by pairwise F-tests with Holm correction (R Foundation for Statistical Computing, Vienna, Austria).

Results

For the uncorrected velocity data, mean difference and 95% limits of agreement (LoA) of flow measurements were as follows: 0.24 (-1.22, 1.71) L/min for arterial vs. venous flow, -0.14 (-1.66, 1.38) L/min for pre- vs. post-bifurcation flow, and 0.09 (-1.44, 1.62) overall. For the manually corrected velocity data, mean difference and 95% LoA were as follows: -0.04 (-0.33, 0.25) L/min for arterial vs. venous flow, -0.12 (-0.32, 0.08) L/min for pre- vs. post-bifurcation flow, and -0.07 (-0.34, 0.2) overall. For the automatically corrected velocity data, mean difference and 95% LoA were as follows: 0.0 (-0.4, 0.4) L/min for arterial vs. venous flow, -0.04 (-0.22, 0.13) L/min for pre- vs. post-bifurcation flow, and -0.02 (-0.35, 0.32) overall. A representative visual example of uncorrected, manually-corrected, and automatically-corrected flow measurements is shown in Figure 4. Bland-Altman plots comparing mean difference and LoA are shown in Figure 5. Bartlett’s test comparing all three groups yielded an overall p-value of less than 2.2e-16, while pairwise F-tests with Holm correction resulted in p<2.2e-16 for uncorrected vs. manually corrected data, p<2.2e-16 for uncorrected vs. neural network corrected data, and p=0.21 for manually corrected vs. automatically corrected data.

Discussion

Following phase-error correction by either manual or CNN-based automated methods, there was improved consistency in flow continuity, observed in comparisons of arterial and venous flow as well as in comparisons of blood flow before and after bifurcations. In a small test population of 8 subjects, there was no statistically significant difference between manual and automatic corrections of background phase offset.

Conclusion

CNNs have the potential to automate background phase-error correction, improving the reliability of quantitative flow measurements in 4D Flow MRI and increasing its accessibility for abdominal vascular applications. We demonstrate the feasibility of training a multichannel 3D U-Net to simultaneously predict velocity field corrections for all three velocity components in a 3D volume, producing inflow-outflow consistency comparable to manual correction. Incorporation of CNN-based automated background phase-error correction into existing visualization and analysis software would streamline the current data processing workflow, improving the utility of 4D Flow MRI as a versatile instrument for clinical diagnosis and research.

Acknowledgements

We acknowledge Microsoft AI for Health for computational resources used for CNN training. A.H. is supported by an ARRS Research Scholarship. M.T.A., S.S.V. and A.H. receive research grant support from GE Healthcare unrelated to this work. S.S.V. and A.H. are co-founders and shareholders of Arterys. E.M.M. is supported by the American Heart Association (Pre-Doctoral Fellowship) and the University of California San Diego Medical Scientist Training Program (NIH/NIHGMS T32GM007198). S.Y. is supported by the University of California San Diego MedGap clinical and translational research training program.

References

  1. Dyverfeldt, P., Bissell, M., Barker, A.J. et al. 4D flow cardiovascular magnetic resonance consensus statement. J Cardiovasc Magn Reson 17, 72 (2015). doi: 10.1186/s12968-015-0174-5
  2. Hope MD, Sedlic T, Dyverfeldt P. Cardiothoracic magnetic resonance flow imaging. J Thorac Imaging. 2013 Jul;28(4):217-30. doi: 10.1097/RTI.0b013e31829192a1.
  3. Pereira VM, Delattre B, Brina O, Bouillot P, Vargas MI. 4D Flow MRI in Neuroradiology: Techniques and Applications. Top Magn Reson Imaging. 2016 Apr;25(2):81-7. doi: 10.1097/RMR.0000000000000082.
  4. Callaghan FM, Burkhardt B, Geiger J, Valsangiacomo Buechel ER, Kellenberger CJ. Flow quantification dependency on background phase correction techniques in 4D-flow MRI. Magn Reson Med. 2020 Jun;83(6):2264-2275. doi: 10.1002/mrm.28085.
  5. Busch J, Giese D, Kozerke S. Image-based background phase error correction in 4D flow MRI revisited. J Magn Reson Imaging. 2017 Nov;46(5):1516-1525. doi: 10.1002/jmri.25668.
  6. Viola F, Dyverfeldt P, Carlhäll CJ, Ebbers T. Data Quality and Optimal Background Correction Order of Respiratory-Gated k-Space Segmented Spoiled Gradient Echo (SGRE) and Echo Planar Imaging (EPI)-Based 4D Flow MRI. J Magn Reson Imaging. 2020 Mar;51(3):885-896. doi: 10.1002/jmri.26879.
  7. Roldán-Alzate A, Francois CJ, Wieben O, Reeder SB. Emerging Applications of Abdominal 4D Flow MRI. AJR Am J Roentgenol. 2016 Jul;207(1):58-66. doi: 10.2214/AJR.15.15995.
  8. Cheng JY, Zhang T, Ruangwattanapaisarn N, et al. Free-Breathing Pediatric MRI with Nonrigid Motion Correction and Acceleration. J Magn Reson Imaging JMRI. 2015;42(2):407. doi: 10.1002/jmri.24785.
  9. Cheng JY, Hanneman K, Zhang T, et al. Comprehensive Motion-Compensated Highly-Accelerated 4D Flow MRI with Ferumoxytol Enhancement for Pediatric Congenital Heart Disease. J Magn Reson Imaging JMRI. 2016;43(6):1355–1368. doi: 10.1002/jmri.25106.
  10. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An Optimal Radial Profile Order Based on the Golden Ratio for Time-Resolved MRI. IEEE Trans Med Imaging. 2007;26(1):68–76. doi: 10.1109/TMI.2006.885337.
  11. Cheng JY, Alley MT, Cunningham CH, Vasanawala SS, Pauly JM, Lustig M. Non-rigid Motion Correction in 3D Using Autofocusing with Localized Linear Translations. Magn Reson Med Off J Soc Magn Reson Med Soc Magn Reson Med. 2012;68(6):1785–1797. doi: 10.1002/mrm.24189.
  12. Ronneberger, Olaf & Fischer, Philipp & Brox, Thomas. (2015). U-Net: Convolutional Networks for Biomedical Image Segmentation. LNCS. 9351. 234-241. Doi: 10.1007/978-3-319-24574-4_28.

Figures

FIGURE 1: Effect of background phase-error correction on flow visualization. In a patient with cirrhosis and severe portal hypertension, a coronal view of the abdomen shows portosystemic shunting through variceal vessels (red arrows) that are difficult to discern in (a) prior to correction, but clearly visualized in (b) following correction. Normal anatomy, including the main portal vein (green arrows), is also better visualized.

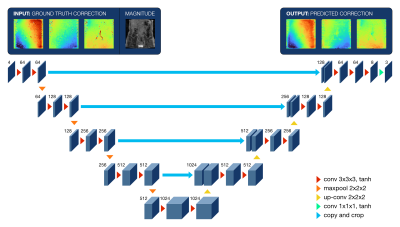
FIGURE 2: Architecture of the 3D multichannel U-Net. The four input channels include manual background phase error corrections with corresponding magnitude images, while the three output channels include predicted corrections for the same three cardinal directions. Numbers indicate the total number of channels. Operations are represented by arrowheads, with kernel size and activation functions indicated in the legend.

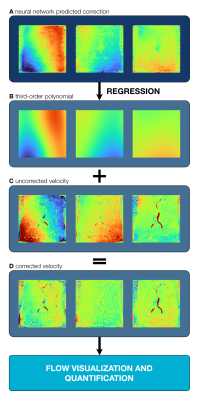
FIGURE 3: Postprocessing pipeline for automated phase-error correction. A representative slice is shown for each of the three cardinal directions. Neural network-predicted corrections are shown in (a), which are reduced with least squares regression to a third-order polynomial approximation in (b). This correction was then added to the (c) original uncorrected data to generate (d) corrected flow data.

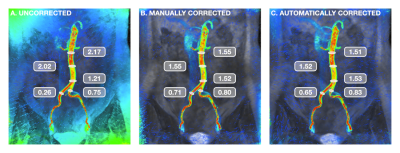
FIGURE 4: Visual example of background phase-error correction. Coronal view of the aorta and common iliac arteries during peak systole, with flow velocity represented by a colormap ranging from red (80 cm/s) to blue (0 cm/s). For assessment of flow continuity, measurements (in L/min) were taken at multiple locations. Corrected velocity measurements demonstrated improved consistency along the length of the infrarenal aorta as well as conservation of mass post-bifurcation.

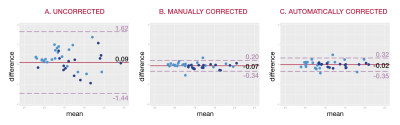
FIGURE 5: Bland-Altman analysis. Consistency of flow measurements are shown for (a) uncorrected velocity data, (b) velocity data corrected manually, and (c) velocity data corrected automatically. Light blue points represent comparisons of arterial and venous flow, while dark blue points represent comparisons of flow before and after vessel bifurcation. Corrected measurements in (b) and (c) demonstrate greater consistency with narrower limits of agreement than seen in (a).

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)
2413