Introduction

Multiple myeloma is a debilitating bone marrow cancer characterised by clonal plasma cells ¹. 140,000 new cases are diagnosed worldwide each year with 106,000 deaths ². Whole-body magnetic resonance imaging (WBMRI) is recognized to be a highly sensitive test; more than one ≥5mm MRI lesion is a myeloma defining event by International Myeloma Working Group diagnostic criteria ³. However, focal bone destruction is a late finding in disease evolution and predated by marrow infiltration. Earlier detection of marrow infiltration on imaging is a clinical gap towards earlier treatment and better outcomes.
Reliable whole-body skeletal segmentation of T1-weighted Dixon gradient-echo images is the first step to measuring marrow fat-fraction as a surrogate metric for marrow infiltration. However, manual segmentation of the skeleton is tedious and subject to inter-and intra-observer variation. Machine learning-based algorithms could be trained for automated fast segmentation, but variable annotation quality (noisy labels) can affect segmentation accuracy with the potential loss of clinically relevant information. We propose an uncertainty-aware 2D U-Net for skeletal marrow segmentation that compensates for noisy ground-truth, improving network performance.

Methods

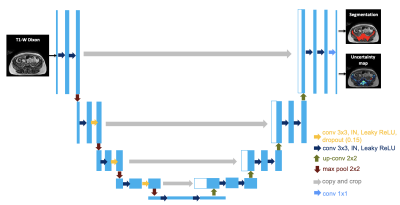
Following institutional review board approval and informed consent, 30 participants with suspected/confirmed myeloma underwent 1.5T whole-body MRI from skull vertex to knees in 5 stations (Magnetom Aera, Siemens Healthineers, Erlangen, Germany). Ground truth skeletal segmentation was performed by two radiologists using axial T1-weighted Dixon gradient-echo images (TR=6.62ms; TE=4.77, 2.39ms; flip angle 10°; NEX=1; FOV 500mm; reconstructed matrix 640, reconstructed voxels=0.8x0.8mm, reconstructed slice thickness=5mm).
We proposed an uncertainty-aware 2D U-Net (uU-Net) (Figure 1). More specifically, three dropout layers with a dropout probability of 15% were added in the intermediate layers of the encoder side of the network. Instance normalization and leaky ReLU was used. Random translate, rotation, and elastic transformation with a horizontal flip were used for data augmentation.
The network was simultaneously trained to output both the logit ($$$f^{W}$$$) and variance ($$$(\sigma^{W})^{2}$$$). To compute the loss function, $$$f^{W}$$$ was corrupted with Gaussian noise with mean 0 and variance $$$(\sigma^{W})^{2}$$$ T times and passed through a sigmoid function to compute the set of corrupted probability maps $$$\hat{Y}=(\hat{Y}_{1},\hat{Y}_{2},...,\hat{Y}_{T})$$$ ⁵.The final loss was the mean of the binary cross-entropy loss computed between each $$$\hat{Y}_{t} (t=1,...T)$$$ and the ground truth.
At inference time, for each input image, T probability and variance maps were generated by means of the Monte Carlo dropout method and the final binary segmentation was computed as the mean of the T probability maps, thresholded at 0.5. Aleatoric and epistemic uncertainty maps were calculated as the mean and variance of the T variance maps. The total uncertainty map was computed as the sum of aleatoric and epistemic uncertainties. T = 20 was set in the experiment.
The performance of our proposed uU-Net for segmenting abdominopelvic stations was compared to the performance of a 2D U-Net (U-Net) with the same architecture as uU-Net but without the uncertainty estimation. Dice coefficient (DSC) was used to assess the accuracy of each generated segmentation. Five-fold cross-validation was employed and the Wilcoxon signed-rank test was used to assess whether the mean DSC of the two approaches differed.

Results

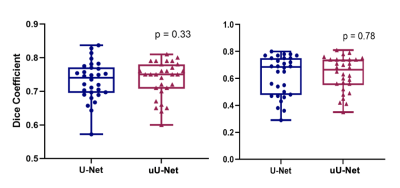
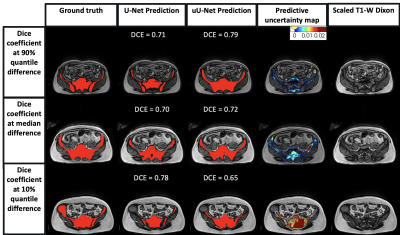
A mean ± standard deviation (SD) DSC of 0.73 ± 0.04 and 0.74 ± 0.03 was obtained for the pelvic station; and 0.62 ± 0.04 and 0.63 ± 0.03 for the abdominal station, for U-Net and uU-Net, respectively.
The box plot of DSC distribution for U-Net and uU-Net is shown in Figure 2. The median (IQR) was 0.74 (0.70, 0.77) and 0.75 (0.71, 0.78), respectively for the pelvic station and 0.69 (0.48, 0.75) and 0.67 (0.56, 0.74), respectively for the abdominal station.There was no significant difference in the two DSC mean distributions (Wilcoxon signed-rank test, p=0.33; p=0.78). Predicted segmentation and uncertainty maps are shown in Figures 3 and 4.

Discussion

Improvement in mean DSC using uncertainty estimates was observed with uU-Net with a narrower range, though this was not statistically significant. This obscures the finding that more accurate segmentation was achieved for the ilium and vertebrae in all patients, which is clinically important.
However, in some patients, over-segmentation of some areas (e.g., incorporation of the sacroiliac joint and sacral foramina) and under-segmentation (e.g., exclusion of ribs) remained. These segmentation errors in part reflect the observer variation in ground-truth labelling, which the predictive uncertainty maps can highlight. By providing a representation of segmentation variance in the training ground truth, expert or machine learning-based modifications can be made to labels to improve network performance.
Nevertheless, there are limitations. First, related to variation-based uncertainty measurement was that the scale was underestimated with predicted pixel values close to either 0 or 1 in T probability maps. Entropy-based estimates could be compared as the next step. Second, related to sample size, though data augmentation and dropout were employed to improve this.

Conclusion

There is a need to improve segmentation robustness. We have proposed an uncertainty-aware 2D U-Net highlighting regional bias in the ground truth. This will allow further refinement of segmentation in high uncertainty regions to improve network performance.

Acknowledgements

This work was supported by the EPSRC Centre for Doctoral Training in Medical Imaging (EP/L015226/1).