Introduction

The lack of one-to-one mapping between RF power and the specific absorption rate (SAR) warrants handling SAR constraints explicitly^1,2 in RF pulse design and exam supervision. Within that context, the Virtual Observation Point (VOP)³ approach was a cornerstone to reduce drastically the number of SAR matrices and make explicit SAR handling tractable. The initial approach³ guaranteed that the SAR at one voxel location with some overestimation would be upper-bounded by the one at another location for every RF pulse. Lee et al⁴ further extended the idea by performing an optimization based on the observation that the SAR at one location could be upper-bounded by different VOPs depending on the RF pulse. The problem for the latter yet is the size of the optimization problem growing with the number of VOPs, which makes the implementation time-consuming and the results more uncertain, given the non-convexity of the problem. Here the generalized VOP scheme is reformulated to obtain a fixed number of optimization variables at each iteration of the compression algorithm, which is shown to boost compression rate.

Methods

Let $$$Q_l$$$ be SAR matrices in W/kg ($$$l=1\cdots N$$$ for the number of voxels), and $$$b$$$ a $$$8\times1$$$ complex vector of modulus 1 representing a normalized RF pulse for a 8-Tx array. The $$$Q$$$ matrices are sorted in descending order according to their maximum eigenvalues. The first one is retained as the first VOP and is called $$$Q_{\mathrm{VOP},1}$$$. At iteration step $$$k$$$, let $$$Q_{\mathrm{VOP}, 1},\cdots,Q_{\mathrm{VOP},N_{\mathrm{VOP}}^{(k)}}$$$ be the VOP list. In Eichfelder’s method, the next VOP candidate $$$Q_k$$$, is added to the VOPs if and only if the domination relation below is not fullfilled:
$$\exists\;l\;\in\{ 1,\cdots, N_{\mathrm{VOP}}^{(k)} \}\;/\;Q_{\mathrm{VOP},l}+\lambda Q_G - Q_k \;\mathrm{psd},$$
where $$$\lambda$$$ is a scalar controlling the overestimation, $$$Q_G$$$ is an Hermitian matrix (here taken as the global SAR matrix) and psd stems for positive semi-definite (all eigenvalues $$$\ge 0$$$). In ref. 4, it has been shown that a higher VOP compression rate (reduced $$$N_{\mathrm{VOP}}$$$ after all $$$Q$$$-matrices have been visited) can be obtained by relaxing the domination criterion as follows: $$$Q$$$ is said to be dominated if there exists $$$(C_1, \cdots,C_{N_{\mathrm{VOP}}^{(k)}})>0$$$ such that:
$$C_1+\cdots+C_{N_{\mathrm{VOP}}^{(k)}}=1,$$
and
$$\left(\sum_{l=1}^{N_{\mathrm{VOP}}^{(k)}} C_l Q_{\mathrm{VOP},l}+\lambda Q_G\right) - Q_k\;\mathrm{psd}.$$
Yet, in this approach, searching at each iteration step $$$k$$$ for the coefficients $$$(C_1,\cdots,C_{N_{\mathrm{VOP}}^{(k)}})$$$ involves an optimization of dimension ($$$N_{\mathrm{VOP}}^{(k)}$$$) that keeps increasing and that can become very large. In this work, we mitigate this problem by searching at each iteration $$$k$$$ a configuration of excitation where the domination fails (reverse approach). If the following condition is met:
$$\exists\;b/\; \forall l\in\{1,\cdots,N_{\mathrm{VOP}}^{(k)}\},\;b^\dagger (Q_k-Q_{\mathrm{VOP},l}-\lambda Q_G) b > 0,$$
then $$$Q_k$$$ is not dominated and should be added to the VOP list. At each iteration of the VOP compression algorithm, the decision to integrate or not the VOP candidate $$$Q_k$$$ boils down to solving the optimization problem:
$$\min_b f_k(b), \mathrm{subject}\;\mathrm{to}\;\|b\|=1,$$
where:
$$f_k(b) = \max_{1\le l\le N_{\mathrm{VOP}}^{(k)}} b^\dagger (Q_{\mathrm{VOP},l}+\lambda Q_G-Q_k) b.$$
The sign of $$$f_k(b)$$$ after optimization then determines the "fate" of $$$Q_k$$$ (VOP or not). The number of variables hence remains 2 times the number of channels of the pTX system (here 8), instead of hundreds or more in the generalized approach. The procedure was tested using electromagnetic simulations of the Nova (Nova medical, Wilmington, MA, USA) 8Tx-32Rx coil provided by the coil manufacturer and run on the Duke head model. Around 110 000 $$$Q$$$-matrices were computed and averaged over 10g of contiguous tissue at 4 mm isotropic resolution. The proposed compression was implemented in Matlab (Mathworks, Natick, MA, USA) using the active-set approach available with the fmincon function, with 5 initial random seeds. It was compared with the generalized approach by Lee et al⁴ for an interval of $$$\lambda$$$ ranging from 0.7 to 1.5. After compression, 10⁶ random RF shims were generated and the true peak SAR value among all voxels versus the values obtained with the different compressed sets were calculated.

Results

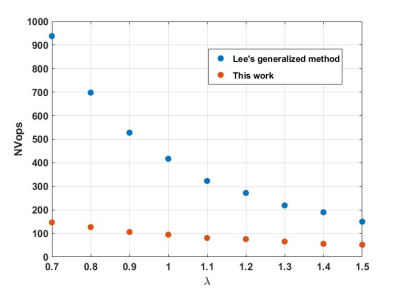
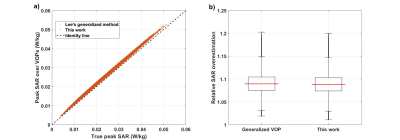
Fig. 1 reports the number of VOPs for each value of $$$\lambda$$$. At $$$\lambda$$$=0.7, the numbers of VOPs are 938 and 147 respectively for Lee’s generalized⁴ approach and the proposed one. Increasing the number of seeds further did not change the number of VOPs, suggesting convergence. Fig. 2 shows the true SAR versus the compressed one calculated with the two methods and for 10⁶ random RF shims. SAR is never underestimated.

Discussion and conclusions

A method to further compress SAR matrices with VOPs was proposed. One important difference with the generalized approach⁴ by Lee and colleagues is the number of optimization variables remaining constant throughout the process, i.e. not scaling with the number of VOPs. Although the mathematical problem is well-posed, our results constitute for the moment strong numerical evidence but no proof for bounding. Not finding $$$b$$$ such that $$$f_k(b)<0$$$ indeed does not imply that such $$$b$$$ does not exist.

Acknowledgements

This work has received funding from the FET-Open H2020 AROMA project (grant number 885876).