2303
A local SAR compression algorithm with improved compression, speed and flexibility1Medical Physics in Radiology (E020), German Cancer Research Center (DKFZ), Heidelberg, Germany, 2Erwin L. Hahn Institute for MRI, University Duisburg-Essen, Essen, Germany, 3High-Field and Hybrid MR Imaging, University Hospital Essen, Essen, Germany, 4Faculty of Physics and Astronomy, University of Heidelberg, Heidelberg, Germany, 5Faculty of Medicine, University of Heidelberg, Heidelberg, Germany
Synopsis
For parallel transmit systems, control of local SAR is very important to ensure safety. For pulse calculation and online supervision, compression of the SAR matrices is used to reduce calculation effort. The original clustering method by Eichfelder et al. was later outperformed by a method proposed by Lee et al. We propose an enhancement to Lee’s algorithm that further increases compression efficiency, speed and flexibility by iteratively reducing the overestimation.
Introduction
Introduction For parallel transmit systems, control of local SAR is very important to ensure safety. Since calculating SAR over the whole set of SAR matrices obtained from simulations comes with a very high computational cost, compression by clustering around virtual observation points (VOPs) has been proposed by Eichfelder et al. (1). Later, Lee et al. (2) proposed an even more efficient compression method without clustering that can outperform Eichfelder’s method by an order of magnitude in terms of compression efficiency. Yet, Lee’s method still leaves room for improvement since it produces redundant VOPs. We present an enhanced method that improves compression efficiency and speed at the same time (3).Methods
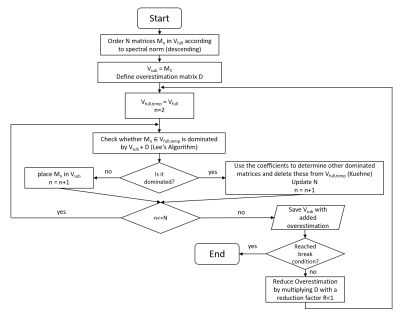
We propose an enhanced algorithm that can reduce the redundant VOPs by iteratively reducing the overestimation. An overview of the algorithm is shown in Figure 1. In its core, the algorithm uses Lee’s algorithm together with a speed enhancement proposed by Kuehne et al. (4). It starts by sorting all matrices by their respective highest eigenvalue in decreasing order. The matrix with the highest eigenvalue is used as the first matrix in the subset Vsub. A matrix for the overestimation term is chosen, which can for example be derived from global SAR (2), local SAR (5) or simply be a diagonal matrix. Then Lee’s algorithm is run with Kuehne’s expansion. Instead of finishing the VOP calculation after completing a run of Lee’s algorithm, the resulting subset Vsub containing the matrices identified as VOPs (but without overestimation) is used at the start of a rerun of the algorithm with the full set of matrices, but with an overestimation lowered by multiplying with a factor R compared to the previous run. After each run of Lee’s algorithm, the resulting set of VOPs can be saved and represents a valid solution for the compression with its respective overestimation.To compare the enhanced algorithm to Lee’s original algorithm, the SAR matrices of three different arrays made from micro strip lines with meanders (6) and operating at the proton resonance frequency of 7 Tesla were used. The first array is a local 8-channel array placed directly on the body (7), while the second and the third array are remotely positioned behind the bore liner in a 2x4-channel and 1x16-channel configuration, respectively (Fig. 2). All simulations were performed in CST Microwave Studio 2017 (CST AG, Darmstadt, Germany).
The algorithms were implemented in Matlab (The Mathworks Inc., Natick, MA, USA) with a high degree of vectorization and other optimizations to speed up the calculations.
The enhanced algorithm is compared to the exact same implementation of Lee’s algorithm as used in the core loop of the enhanced algorithm to minimize the influence of the implementation on timing differences between the algorithms. In both cases, the overestimation is defined by a diagonal matrix with all diagonal elements equal to a fraction of the worst-case local SAR.
Results
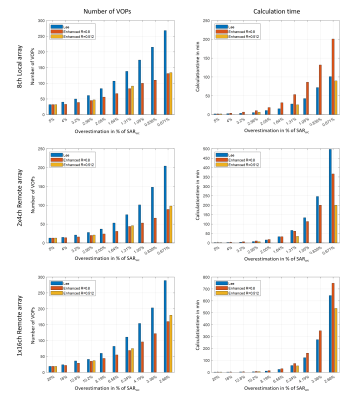
Figure 3 shows the comparison between Lee’s algorithm and the enhanced algorithm for all three arrays. The left column shows the resulting number of VOPs for different overestimations given in percent of the worst-case local SAR, while the right column shows the time necessary to calculate the results. Two different reduction factors R were used.The results show in all cases that after very few iterations the enhanced algorithm approximately halves the number of VOPs compared to the original algorithm. The smaller reduction factor R performs slightly better.
The effect on calculation time in the right column of Figure 3 shows a strong dependence on the array model. While the higher R value (smaller reduction step) takes approximately twice the calculation time as Lee’s algorithm for the 8-channel local array, it is faster for the 2x4-channel remote array. The larger reduction step (lower R value) proved to be faster in all cases. It should be noted that the duration given for the calculation time of the enhanced algorithm includes the calculation of all previous intermediate results.
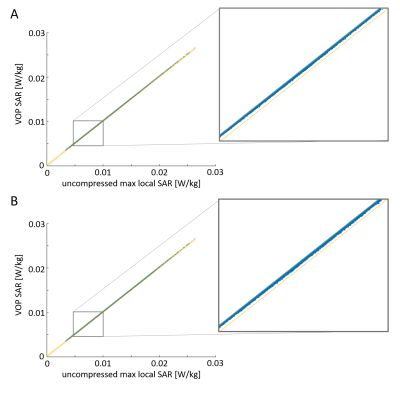
Figure 4 shows scatter plots for local SAR results of the compressed data versus the results of the uncompressed data for the 8-channel local array for one million random excitation vectors.
No underestimation occurred in any scenario.
Discussion
The results show that the proposed algorithm is capable of approximately halving the number of VOPs for a certain overestimation. When the reduction factor R is chosen carefully, the enhanced algorithm is also faster than the original algorithm. The reason for this is twofold; firstly, a lower number of VOPs makes the optimization in Lee’s algorithm faster when trying to find the coefficients to dominate a certain matrix; secondly, the search for other dominated matrices in the step introduced by Kuehne finds more matrices that are dominated during the first runs of Lee’s algorithm, making successive runs faster.Conclusion
The presented algorithm is an expansion of the algorithm presented by Lee et al. It significantly reduces the number of VOPs for a given overestimation while at the same time being potentially faster. Furthermore, the algorithm has more flexibility because it provides intermediate results that are valid VOP sets with an overestimation decreasing with each iteration step.Acknowledgements
The authors would like to thank Emil Orzada, whose constant search for Lego® blocks with intermediate sorting during home office inspired the idea for the presented algorithm.References
1. Eichfelder G, Gebhardt M. Local specific absorption rate control for parallel transmission by virtual observation points. Magn Reson Med 2011;66(5):1468-1476.
2. Lee J, Gebhardt M, Wald LL, Adalsteinsson E. Local SAR in parallel transmission pulse design. Magn Reson Med 2012;67(6):1566-1578.
3. Orzada S, Fiedler TM, Quick HH, Ladd ME. A local SAR compression algorithm with improved compression, speed and flexibility. 2020;(Submitted to MRM).
4. Kuehne A, Waiczies H, Niendorf T. Massively accelerated VOP compression for population-scale RF safety models. Proc Intl Soc Mag Reson Med 26 2017:478.
5. Orzada S, Fiedler TM, Bitz AK, Ladd ME, Quick HH. Local SAR compression with overestimation control to reduce maximum relative SAR overestimation and improve multi-channel RF array performance. MAGMA 2020.
6. Rietsch SHG, Quick HH, Orzada S. Impact of different meander sizes on the RF transmit performance and coupling of microstrip line elements at 7 T. Med Phys 2015;42(8).
7. Orzada S, Quick HH, Ladd ME, Bahr A, Bolz T, Yazdanbakhsh P, Solbach K, Bitz AK. A flexible 8-channel transmit/receive body coil for 7 T human imaging. In: Proceedings of the 17th scientific meeting, International Society for Magnetic Resonance in Medicine, Honolulu, p 2999 2009.
8. Christ A, Kainz W, Hahn EG, Honegger K, Zefferer M, Neufeld E, Rascher W, Janka R, Bautz W, Chen J, Kiefer B, Schmitt P, Hollenbach HP, Shen J, Oberle M, Szczerba D, Kam A, Guag JW, Kuster N. The Virtual Family--development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol 2010;55(2):N23-38.
Figures
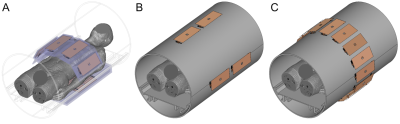
Coil simulation models for generating the SAR matrices. A) local 8-channel array, B) remote 2x4-channel array, and C) remote 1x16-channel array.
A heterogeneous body model (male, 174 cm, 70 kg, tissue resolution 2x2x2 mm³) (8) was used for all arrays. Matrices for 10 g-averaged local SAR were calculated for all three setups resulting in 7.6 million matrices for the 8-channel local array, 6.5 million matrices for the 2x4-channel remote array, and 6.2 million for the 1x16-channel remote array.