Introduction

Individual differences in head shape and size, variations in padding material options within and across scanners, and circumstantial adjustments (e.g. extra padding to reduce discomfort) lead to variations in patient positioning. Virtual observation points¹ or Q-matrices² are often provided with parallel transmit (pTx) radiofrequency (RF) coils to enable local specifical absorption rate (SAR) supervision. However, these safety models -whether generated at one or multiple positions- are insensitive to the current patient positioning. On the contrary, patient specific RF pulses are designed using B₁⁺-sensitivity maps that are position dependent. This study investigates the effect of this positional mismatch between safety models and B₁⁺-maps on local SAR estimation.

Methods

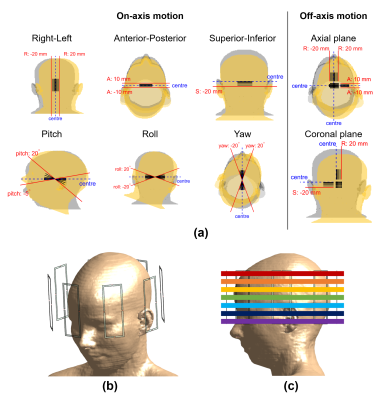
Electromagnetic (EM) simulations were performed using Sim4Life (ZMT, Zurich, Switzerland) using the virtual body model Ella³ for 163 different relative positions of the body model with respect to the 8-channel generic coil structure (Figure 1). These included on/around axis displacements/rotations of 1/2/5/10/15/20 mm/degrees and off-axis displacements (axial/coronal planes). Cases (in axial, pitch) that would overlap coil elements and the model were excluded.

Entries of the Q-matrices² were averaged over 10-grams of tissue with cubical volumes⁴. Small-tip-angle 1-/2-/3-/4-/5-spokes pulses were designed using Matching Pursuit guided Conjugate Gradient^5,6 for seven slices (from cerebellum to crown) at each position – yielding 5705 pulses. Channel coefficients were re-optimized with the addition of each spoke. The peak spatial (local) SAR (psSAR) of each pulse was evaluated using the body models

• (i) at the position the pulse was designed for (psSAR-actual),
• (ii) at centre (psSAR-centre),
• (iii) at centre and A=±5mm, A=±10mm, R=±5mm, R=±10mm and highest was used (9 models; psSAR-9positions).

By comparing (i)-(ii) and (i)-(iii), the effect of the positional mismatch on psSAR was quantified. Details omitted here follow⁶.

Results

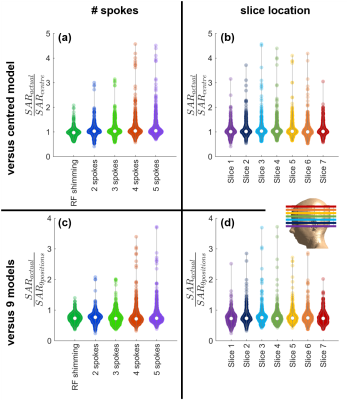
Positional mismatch between the B₁⁺-maps used for pulse design and Q-matrices used for safety evaluations led to up to 78% underestimation of peak local SAR. The sensitivity of SAR to positional mismatch increased with increasing pulse complexity. Actual SAR was up to 2.1-fold higher than the estimated peak for RF shimming (1-spoke) and 4.6-fold higher for 4-/5-spokes pulses (Figure 2a-b).

The sensitivity of local SAR to positional mismatch was not specific to any part of the brain (Figure 2b). Two-sample t-test comparison of slices showed insignificant variation in 15 of 21 comparisons.

Using 9 body models to calculate psSAR reduced the positional mismatch sensitivity (Figure 2c-d). Nevertheless, the actual psSAR was still up to 3.7-fold higher than the estimate.

Figure 3 shows the maximum sensitivity of local SAR to positional mismatch across slices and spokes at each axial position (rotations and coronal results omitted here). Actual SAR exceeded the estimate at all positions, and by more than 50% at 40% of the positions. Using 9 models (arrows) to estimate psSAR benefitted the majority of positions close to these positions. However, this benefit comes at the cost of over-conservative SAR estimations: the peak local SAR of pulses designed for the centred position was overestimated by 54% with these 9 models.

Figure 3 is the maximum intensity projection across spokes and slices. Therefore, the effect of using 9 models varies across positions; i.e. the worst-case of 4.5 was for 4 spokes (panel-a) whereas 3.7 was for 5 spokes (panel-b). Hence, SAR reduction varies spatially.

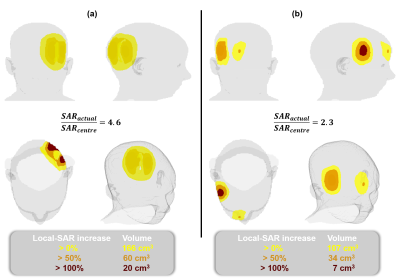
The actual local SAR was 4.6-fold as high as the estimate and a region of 20 cm³ was exposed to more than twice the estimated peak at the worst case (Figure 4a). Figure 4b shows another case where the right-anterior part of the head observes actual local SAR greater than SAR-centre.

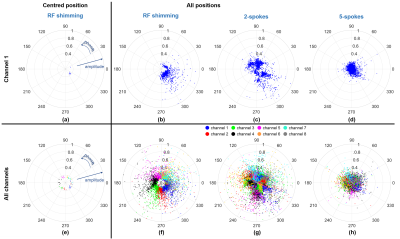
As the pulse gets more complex (more spokes), the sensitivity of SAR to positional mismatch increases. This is attributed to the much higher variation in coil coefficients for more spokes (Figure 5). For RF shimming at the centred position, all coils have minimal variation in amplitude and well-defined phase “zones” across the slices. Therefore, the SAR-related interaction between coil elements will vary less. When all positions are investigated though, the variation in amplitude increases substantially while the phase “zones” remain intact. When more spokes are added, the “zones” diffuse; and coil coefficients and consequently SAR patterns become more varied across positions, leading to unpredictable SAR-actual/SAR-centre behaviour.

Discussion

Patient specific pulses use B₁⁺-maps that are inherently position dependent. However, scanners/coils have fixed safety models. This creates potential safety hazards as positional mismatches lead to up to 4.6-fold higher actual SAR than the estimated peak.

Using more models reduces the risk of exceeding the estimates and using all positions would minimize it. However, much like using maximum eigenvalues being over-conservative⁶, this solution would be over-conservative (>4.6 safety margin implied here) to the degree that would outweigh the benefit of parallel-transmit. Calculating the SAR of a pulse designed for R:-20mm A:-5mm at the opposite corner R:20mm A:10mm would likely yield even a higher ratio, unnecessarily constraining SAR even further for an unrealistic scenario. A feasible approach might be to estimate the position of a participant (e.g. via localizer images) and use the models/positions that closely enclose the estimated position to ensure safety while minimizing over-estimation. This can also be extended to real-time adjustment of safety models in case of motion⁶.

Acknowledgements

No acknowledgement found.