2254
Orientation dependence of T2 in newborn white matter shows dipole-dipole interaction effects1Department of Physics & Astronomy, University of British Columbia, Vancouver, BC, Canada, 2UBC MRI Research Centre, University of British Columbia, Vancouver, BC, Canada, 3Department of Neuroradiology, Medical University of Innsbruck, Innsbruck, Austria, 4Department of Neurology, Medical University of Graz, Graz, Austria, 5Department of Radiology, Children's Hospital of Chongqing Medical University, Chongqing, China, 6Ministry of Education Key Laboratory of Child Development and Disorders, Chongqing Medical University, Chongqing, China, 7Key Laboratory of Pediatrics in Chongqing, Chongqing Medical University, Chongqing, China, 8Chongqing International Science and Technology Cooperation Center for Child Development and Disorders, Chongqing, China, 9Division of Neurology, Department of Pediatrics, University of British Columbia, Vancouver, BC, Canada, 10Department of Radiology, University of British Columbia, Vancouver, BC, Canada
Synopsis
In adult White Matter (WM), tissue orientation effects on $$$R_2$$$ are best described by diffusion within field inhomogeneities created by the myelin sheath. Here we studied how $$$R_2$$$ relaxation depends on white matter fibre orientation in the human newborn brain in vivo. We found that the orientation dependency is very different from adults and best described by a model of dipole-dipole interaction.
Introduction
Tissue orientation effects in $$$R_2=\frac{1}{T_2}$$$ relaxation are well known in tissues rich in collagen fibers such as tendons and cartilage.1,2 The source of the orientation dependence in those tissues are dipole-dipole interactions between water molecules aligned along the parallel filaments which can be modelled as$$R_2^{\text{dip-dip}}=c_{\text{orientation independent}}+c_{\text{dip-dip}}\left(3\cos\left(\theta\right)-1\right)^2.$$
The dipole-dipole interaction results in a characteristic minimum at angles of $$$54.7^{\circ}$$$ for which the orientation dependent term vanishes.2 Orientation effects of the MRI signal in the human brain have been widely studied for $$$R_2^*$$$ relaxation and are attributed to the susceptibility differences between cylindrical myelin sheaths and the surrounding water as well as the anisotropic susceptibility of myelin.3-11As the effect of local susceptibility differences on stationary spins is removed in spin echo sequences, orientation effects in $$$R_2$$$ in WM are smaller, but have also been observed.3,12,13 Similar to $$$R_2^*$$$, $$$R_2$$$ was found to be minimal in fibers parallel to $$$B_0$$$ and to increase as the angle increases to $$$90^{\circ}$$$. The effect is attributed to diffusion of spins through the field inhomogeneities created by the myelin sheaths and, to a small degree, the interaction of susceptibility related fields with applied imaging gradients.14 It is not clear, however, whether dipole-dipole interaction effects are absent in brain tissue or whether they are overshadowed by the magnetic susceptibility effects.3 To address this question we measured the orientation dependency in the unmyelinated human newborn brain in vivo.
Methods
Eight healthy subjects (gestational age $$$40.1\pm 1.1$$$ weeks) were scanned at 3T. $$$R_2$$$ data were acquired with a 32-echo 3D GRASE sequence (1st $$$T_E=10\,\text{ms}$$$, $$$\Delta T_E=10\,\text{ms}$$$, $$$T_R=4300\,\text{ms}$$$).15 Fiber orientation was mapped with diffusion tensor imaging (DTI). The spin echo data were analyzed using DECAES16 and $$$T_2$$$ was computed as the geometric mean $$$T_2$$$ using a $$$T_2$$$ range of $$$8\,\text{ms}$$$ to $$$2.0\,\text{s}$$$. $$$R_2$$$ was plotted as a function of fiber angle pooling voxels according to their orientation in $$$5^{\circ}$$$ intervals. Models of dipole-dipole interaction, diffusion related dephasing and the model of diffusion and field gradients14 were fitted to $$$R_2(\theta)$$$.Results
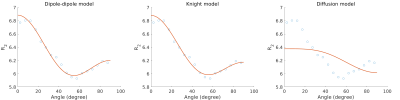
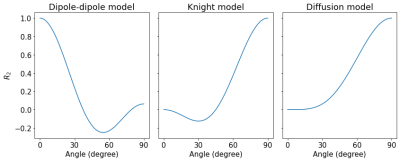
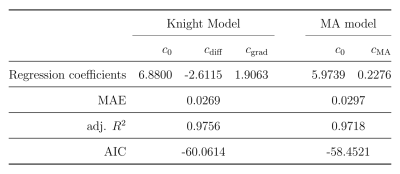
The average myelin water fraction of the neonate subjects is in the expected range for newborns with $$$1.7\%$$$. $$$R_2$$$ as a function of angle is shown in Figure 1. Figure 2 shows the orientation dependencies predicted by the dipole-dipole model, Knight’s model (which includes an imaging gradient term), and the diffusion-only model. The coefficients of the best fits, as well as adjusted $$$R^2$$$, Mean Absolute Error (MAE), and the Akaike Information Criterion (AIC) are shown in the table in Figure 3. While the diffusion-only model fails to fit the data, the dipole-dipole model and the model by Knight fit the data well.Discussion
Both the dipole-dipole interaction model and the model by Knight et al. (diffusion plus effects of imaging gradients) fit the observed data well. However, the model by Knight assumes the presence of magnetic susceptibility differences in myelin sheaths and it only fits the data with a large coefficient for the imaging gradient term, which is not realistic. Furthermore, the simpler model of dipole-dipole interaction which only has a single orientation dependent term, fits the data almost as well as Knight’s model. For these reasons we suggest that the orientation dependency of $$$R_2$$$ in the newborn brain is due to dipole-dipole interaction. This interpretation is consistent with the absence of myelin in newborns and it implies the alignment of water molecules with elongated structures. Two primary candidates for hydrated filaments that might be associated with such structured water in human WM are the microtubule and neurofilaments within the axon. Both are known to be present in the newborn brain.Conclusion
The orientation dependence of $$$R_2$$$ in neonate WM shows opposite trends when compared to adult data and is well described by the model of dipole-dipole interaction. The source of the orientation dependence is therefore more likely to be structured water associated with filaments in axons rather than magnetic susceptibility differences which dominate the orientation dependence of $$$R_2$$$ in adult WM, but are largely absent in the newborn brain.Acknowledgements
No acknowledgement found.References
1. Haenninen N, et al. Orientation anisotropy of quantitative MRI relaxation parameters in ordered tissue. Scientific Reports. 2017;7:9606.
2. Bydder M, et al. The Magic Angle Effect: A Source of Artifact, Determinant of Image Contrast, and Technique for Imaging. Journal of MRI. 2007;25:290–300.
3. Oh S.-H. et al. Origin of B0 orientation dependent R2∗ (= 1/T2∗) in white matter. NeuroImage. 2013;73:71–79.
4. Bender B, and Klose U. The in vivo influence of white matter fiber orientation towards B0 on T2∗ in the human brain. NMR Biomed. 2010;23:1071–1076.
5. Denk C, et al. The influence of white matter fibre orientation on MR signal phase and decay. NMR Biomed. 2011;24:246–252.
6. Lee J, et al. T2*-based fiber orientation mapping. NeuroImage. 2011;57(1):225–234.
7. Lee J, et al. Mechanisms of T2∗ anisotropy and gradient echo myelin water imaging. Magn Res Med. 2016;30:e3513.
8. Lee J, et al. An R2∗ model of white matter for fiber orientation and myelin concentration. NeuroImage. 2017;162:260–275.
9. Weber A, et al. Myelin water imaging and R2∗ mapping in neonates: Investigating R2∗ dependence on myelin and fibre orientation in whole brain white matter. NMR in Biomedicine. 2019;e4222.
10. Hernández-Torres E, et al. Orientation Dependent MR Signal Decay Differentiates between People with MS, Their Asymptomatic Siblings and Unrelated Healthy Controls. PLoS ONE. 2015;10(10):e0140956.
11. Kor D, et al. The role of iron and myelin in orientation dependent R2∗ of white matter. Magn. Res. Med. 2019; e4092.
12. Knight M, et al. Anisotropy of spin-echo T2 relaxation by magnetic resonance imaging in the human brain in vivo. Biomedical Spectroscopy and Imaging. 2015;4:299–310.
13. Birkl C, et al. Myelin water imaging depends on white matter fiber orientation in the human brain, Magn Res Med. 2020;00:1–11.
14. Knight M, et al. Magnetic Resonance Relaxation Anisotropy: Physical Principles and Uses in Microstructure Imaging. Biophysical Journal. 2017;112:1517–1528.
15. Prasloski T, Rauscher A, et al. Rapid whole cerebrum myelin water imaging using a 3D GRASE sequence. NeuroImage. 2012;63(1):533-9.
16. Doucette J, et al. DECAES – DEcomposition and Component Analysis of Exponential Signals. Z Med Phys. 2020;30(4):271–278.
Figures