2211
Constrained Optimized Water Suppression (COWS) for 1H Magnetic Resonance Spectroscopy1Biomedical Engineering, Columbia University, New York City, NY, United States, 2Radiology, Columbia University, New York City, NY, United States
Synopsis
Water suppression is a necessary component to magnetic resonance spectroscopy experiments due to its roughly 5000-fold higher intensity than the metabolites of interest. Here we introduce a novel algorithm for water suppression which operates in a similar manner to that originally proposed by WET and expanded upon by VAPOR, but is flexible in that it can accommodate an arbitrary number of RF pulses, minimum duration between pulses, total module duration and maximum flip angles. This method is referred to as Constrained Optimized Water Suppression. We demonstrated the improvement of COWS over the gold standard VAPOR in simulations and in vivo.
Introduction
The concentration of water is ~5000x larger than the concentration of metabolites in in vivo MRS, thus to visualize and quantify the metabolites water suppression (WS) modules substantially reduce the measured water signal. The gold standard for water suppression is Variable Power Radio Frequency Pulses with Optimized Relaxation Delays1 (VAPOR). Although outstanding WS was attained in the original VAPOR manuscript1 and certain subsequent implementations2–5, there can be found numerous examples in the literature of suboptimal WS with VAPOR6–8, and as such subsequent modules have been developed in an attempt to out-perform VAPOR, such as HGWS7. Additionally, even VAPOR schemes which have been shown to provide high-quality water suppression in metabolite scans5 result in poor water suppression for macromolecule spectra due to the double-inversion preparation module9. Constrained Optimized Water Suppression (COWS) enables the optimization of a WS scheme tailored to the details of the MRS experiment at hand with number of RF pulses, minimum duration between pulses, total module duration and maximum flip angles as input constraints. An implementation of the COWS algorithm has been made available to the scientific community free of charge (http://innovation.columbia.edu/technologies/CU21111_COWS).Methods
COWS AlgorithmThe longitudinal magnetization after a series of n RF pulses can be expressed as10,11 $$M_z^n(\boldsymbol{\tau},\boldsymbol{\theta},T_1,F_B)=M_z^{n-1}\text{cos}(F_B\theta_n)e^{-\tau_n/T_1}+M_z^{eq}(1-e^{-\tau_n/T_1}), [1]$$
where $$$T_1$$$ is the longitudinal relaxation time, if n=0 then $$$M_z^0$$$ is the longitudinal magnetization prior to the pulse, $$$M_z^{eq}$$$ is the equilibrium longitudinal magnetization and $$$F_B$$$ is the B1 overdrive factor (i.e., the factor by which the flip angle deviates from its nominally prescribed value due to B1 inhomogeneities), $$$\boldsymbol{\theta}$$$ and $$$\boldsymbol{\tau}$$$ are the vectors of the flip angles and delays after the pulse. The initial value for the longitudinal magnetization prior to the WS module, $$$M_z^{0,initial}$$$ is assumed to be equal to $$$M_z^{eq}$$$.
The cost function for COWS is $$ C(\boldsymbol{\tau},\boldsymbol{\theta}) = \sum_{i=1}^{N_{T_1}} \sum_{j=1}^{N_{F_B}}M_z^n(\boldsymbol{\tau},\boldsymbol{\theta},T_{1,i},F_{B,j})\text{exp}\left(-\left(\frac{T_{1,i}-\bar{T_1}}{W_{T_1}}\right)-\left(\frac{F_{B,j}-\bar{F_B}}{W_{F_B}}\right)\right), [2]$$
where $$$M_z^n$$$ is calculated via Equation 1, $$$T_{1,i}$$$ is the ith $$$T_1$$$ value, and $$$F_{B,j}$$$ is the jth B1 overdrive factor. The exponential is a Gaussian weighting function to provide greater weight to the values closer to the mean values and the overbar is used to denote the mean. The optimized flip angles and delays were then calculated via $$[^{cows}\boldsymbol{\tau},^{cows}\boldsymbol{\theta}] = \text{argmin}_{\boldsymbol{\tau},\boldsymbol{\theta}}\left(C(\boldsymbol{\tau},\boldsymbol{\theta})\right). [3] $$
The numerical optimization was performed using the active set method with constraints in MATLAB (Mathworks, Natick, MA) R2013b.
COWS Modules
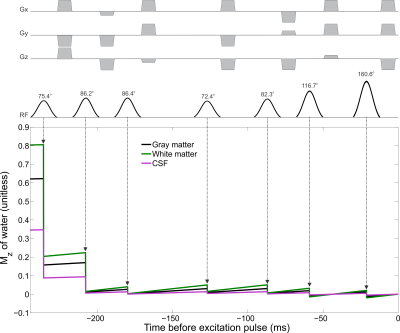
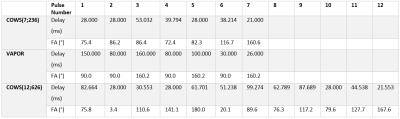
Two COWS WS modules were developed and tested here. The first utilized 7 pulses, similar to VAPOR1, but with substantially reduced module duration (236 ms), referred to as COWS(7;236). The second employed an equal module duration to VAPOR (626 ms), but utilized 12 pulses, referred to as COWS(12;626). The default values $$$W_{T_1} = 3 s$$$ and $$$W_{F_B} = 0.1$$$ were used and the range of values considered were $$$0.5 s \leq T_1 \leq 5.0 s $$$ and $$$0.75 \leq F_B \leq 1.25$$$. The minimum duration of 28 ms between successive WS pulses, and 21 ms duration between the final water suppression pulse and the excitation pulse were used due to experimental constraints. The crusher scheme to dephase all water coherence pathways is automatically obtained from COWS via DOTCOPS12,13. The pulse sequence for COWS(7;236) and conceptual diagram of action is given in Figure 1.
The water suppression efficiency was calculated as $$f_{ws} =\frac{\text{max}(|S_{sup}|)}{\text{max}(|S_{unsup}|)}, [4]$$
where $$$|S_{sup}|$$$ is the absolute (i.e., magnitude) spectrum with the water suppression module on in the spectral range of water (4.60 to 4.70 ppm) and $$$|S_{unsup}| $$$ is absolute spectrum of the water reference.
Experimental Validation
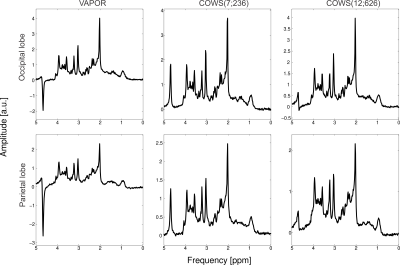
One healthy subject was scanned with informed consent with TE/TR = 20 ms/2000 ms sLASER5,14,15 acquisition at Siemens Prisma 3 T (Siemens Healthineers, Erlangen, Germany) with 32-channel head coil. Metabolite spectra in the occipital and prefrontal lobe were collected using three WS schemes: VAPOR, COWS(7;236) and COWS(12;626). Macromolecule spectra obtained with a double inversion preparation module, TI1 = 920 ms, TI2 = 330 ms in the parietal lobe were also acquired using VAPOR and COWS(7;236).
Results and Discussion
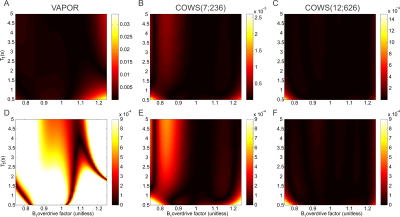
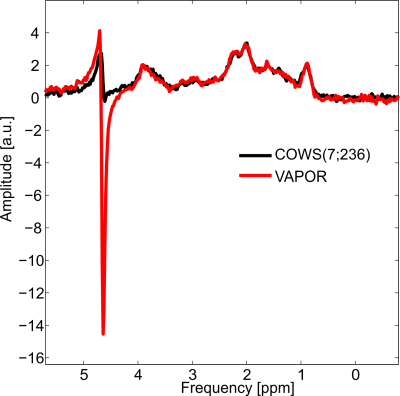
The flip angles (FA), delays for both COWS schemes and the VAPOR implementation are given in Table 1. Bloch simulations demonstrate COWS(7;236) and COWS(12;626) demonstrate substantially improved water suppression over the range of simulated $$$T_1$$$ and $$$B_1$$$ values (Figure 2). The specific absorption rate (SAR) compared to VAPOR was 0.66 and 1.36 for COWS(7;236) and COWS(12;626), respectively. Substantially improved water suppression was obtained for both the metabolite and macromolecule voxels (Figure 3). The water suppression efficiency was 0.22%/0.22%/0.08% for VAPOR, COWS(7;236) and COWS(12;626, respectively, for the occipital lobe, and, 0.29%/0.15%/0.06% for the parietal lobe. VAPOR and COWS(7;236) had comparable performance despite the substantially reduced module duration and reduced SAR, and substantial improvement of COWS(12;626) over VAPOR which have equal module duration. The macromolecule spectra acquired with double inversion recovery nulling of metabolites from COWS had considerably reduced residual water (Figure 4), with a water suppression efficiency of 2.43% for VAPOR and 0.57% for COWS(7;236).Conclusions
A WS algorithm was developed and tested versus the current state-of-the-art WS scheme, VAPOR. Improved water suppression was demonstrated for both schemes, with COWS(12;626) providing the WS of choice for metabolite spectra. COWS(7;236) provided improved water suppression over VAPOR for macromolecule spectra, with a substantially reduced modulate duration.Acknowledgements
This work was performed at Zuckerman Mind Brain Behavior Institute MRI Platform, a shared resource and Columbia MR Research Center site.References
1. Tkáč, I., Starcuk, Z., Choi, I. Y. & Gruetter, R. In vivo 1H NMR spectroscopy of rat brain at 1 ms echo time. Magn Reson Med 41, 649–56 (1999).
2. Oz, G. & Tkac, I. Short-echo, Single-shot, Full-indensity 1H MRS For Neurochemical Profiling at 4T: Validation in the Cerebellum and Brainstem. Magn Reson Med 65, 1–19 (2011).
3. Deelchand, D. K., Joers, J. M., Auerbach, E. J. & Henry, P.-G. Prospective motion and B0 shim correction for MR spectroscopy in human brain at 7 T. Magn Reson Med 00, 1–9 (2019).
4. Deelchand, D. K. et al. In vivo 1H NMR spectroscopy of the human brain at 9.4T : Initial results. J Magn Reson 206, 74–80 (2010).
5. Landheer, K., Gajdosik, M. & Juchem, C. Semi-LASER Single-Voxel Spectroscopic Sequence with Minimal Echo Time of 20 ms in the Human Brain at 3 T. NMR Biomed e4324 (2020).
6. Landheer, K. & Juchem, C. Dephasing optimization through coherence order pathway selection (DOTCOPS) for improved crusher schemes in MR spectroscopy. Magn Reson Med 81, 2209–2222 (2019).
7. Chan, K. L., Ouwerkerk, R. & Barker, P. Water suppression in the human brain with hypergeometric RF pulses for single-voxel and multi-voxel MR spectroscopy. Magn Reson Med 80, 1298–1306 (2018).
8. Henning, A., Fuchs, A., Murdoch, J. B. & Boesiger, P. Slice-selective FID acquisition, localized by outer volume suppression (FIDLOVS) for 1H-MRSI of the human brain at 7 T with minimal signal loss. NMR Biomed 22, 683–696 (2009).
9. Landheer, K., Gajdosik, M., Treacy, M. & Juchem, C. Concentration and T2 Relaxation Times of Macromolecules at 3 Tesla. Magn Reson Med 84, 2327–2337 (2020).
10. Ogg, R. J., Kingsley, P. B. & Taylor, J. S. WET, a T1- and B1-Insensitive Water-Suppression Method for in Vivo Localized 1H NMR Spectroscopy. J Magn Reson Ser B 104, 1–10 (1994).
11. Malcom H. Levitt. Spin Dynamics. (Wiley, 2008).
12. Landheer, K. & Juchem, C. Dephasing optimization through coherence order pathway selection - DOTCOPS. http://innovation.columbia.edu/technologies/CU18146_DOTCOPS
13. Landheer, K. & Juchem, C. Simultaneous optimization of crusher and phase cycling schemes for magnetic resonance spectroscopy: an extension of dephasing optimization through coherence order pathway selection. Magn Reson Med 83, 391–402 (2020).
14. Scheenen, T. W. J., Klomp, D. W. J., Wijnen, J. P. & Heerschap, A. Short echo time 1H-MRSI of the human brain at 3T with minimal chemical shift displacement errors using adiabatic refocusing pulses. Magn Reson Med 59, 1–6 (2008).
15. Garwood, M. & DelaBarre, L. The Return of the Frequency Sweep: Designing Adiabatic Pulses for Contemporary NMR. J Magn Reson 153, 155–177 (2001).
16. Stanisz, G. J. et al. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med 54, 507–12 (2005).
Figures