Purpose

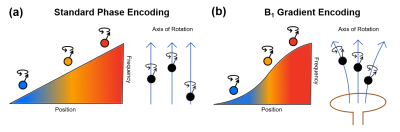
If it were possible to eliminate the need for B₀ gradients in MRI, the benefits would include cost-savings, increased bore space, and silent scanning¹. At low field where SAR constraints are reduced, spatial encoding with RF field gradients instead of B₀ gradients is a viable option^1-7. However, one challenge is creating efficient RF coils capable of producing linear B₁ gradients for Fourier imaging (Fig. 1). To produce sufficient B₁ amplitudes over the object required for spatial encoding, surface coils are often used as RF transmitters in RF-encoding methods⁸. To minimize image distortions, the object is usually confined to the approximately linear region of the surface coil’s B₁ profile, which is less than ideal¹. In this work, we investigate whether an established method to correct distortions in conventional MRI can be repurposed to correct distortions arising from the nonlinearity of B₁ gradients when performing RF-encoded MRI. Although several⁹ methods are capable of correcting image distortions arising from nonlinear B₀ gradients and/or large B₀ inhomogeneity, here we chose to adapt the method of Weis et al¹⁰. Through theory and simulations, we demonstrate the ability to correct image distortions arising from nonlinear B₁ gradients in RF-encoded MRI.

Methods

The signal (\(s\left(n\right)\)) from the basic RF gradient encoding sequence considered here, namely rotating frame zeugmatography (RFZ), can be described similarly to a 1D phase encoding experiment in standard MRI, with the difference of substituting the B1 gradient (\(B_{1\ grad}\left(x\right)\)) for the conventional gradient,

\[s\left(n\right)=\int{M_{xy}\left(x\right)exp\left(-i\left(xk_{lin}\left(n\right)+\gamma\Delta B_{1\ grad}\left(x\right)n\tau\right)\right)dx}\text{,}\qquad\textbf{(1)}\]

where we have also taken the additional step of decomposing \(B_{1\ grad}\left(x\right)\) into its linear and nonlinear components: \(B_{1\ grad}\left(x\right)=g_xx+\Delta B_{1\ grad}\left(x\right)\), for reasons that will subsequently be apparent. Here, \(n\in\left[-{\frac{N}{2}\ ,\ }{\frac{N}{2}}-1\right]\) is the index of the phase-encoding step (\(N=256\)), \(\tau\) is the incremental pulse width, and \(k_{lin}\left(n\right)=\gamma\ g_xn\tau\) is the k-space coordinate. Note that though the conventional MRI phase encoding experiment is insensitive to B₀ inhomogeneity, it too is sensitive to gradient nonlinearity. Now we define the distorted coordinate system: \(x^\prime=x\ +\ \Delta B_{1\ grad}\left(x\right)/g_x\); calculate the Jacobian, \(J\left(x\right)=1+\frac{\partial\Delta B_{1grad}\left(x\right)}{\partial x}/g_x\), and using these, minor rearrangement of Eq. 1 yields,
\[s\left(n\right)=\int{M_{xy}\left(x^\prime\right)exp\left(-ik_{lin}\left(n\right)x^\prime\right)J^{-1}\left(x^\prime\right)}dx^\prime\text{,}\qquad\textbf{(2)}\]
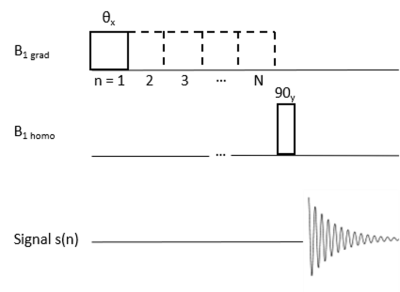
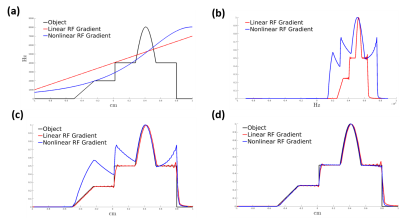
where \(J^{-1}\left(x^\prime\right)\) is the reciprocal of the Jacobian. Application of IFT to Eq. 2, yields the distorted reconstruction: \(I_{dist}\left(x^\prime\right)=M_{xy}\left(x^\prime\right)J^{-1}\left(x^\prime\right)\). Analyzing this equation, we see that the distortion caused by RF gradient nonlinearity comprises two components: a) a geometric distortion arising from the distorted coordinate (\(x^\prime\)), and b) an intensity distortion described by the reciprocal of the Jacobian (\(J^{-1}(x\prime))\)). Our adapted distortion correction algorithm thus first corrects the geometric distortion via usage of interpolation and then subsequently performs intensity correction by scaling with the Jacobian. To demonstrate this correction method, we modeled a 1D numerical phantom and simulated RFZ using both a linear field and nonlinear field (Fig. 3a). The nonlinear field describes that of a surface coil; it was calculated using the Biot-Savart law. The linear field was designed to place the object in roughly the same range of frequencies as the nonlinear field for comparison purposes. Signal measurements on the numerical phantom were simulated using the pulse sequence depicted in (Fig. 2). Both 1D images (1x256) were then reconstructed via FFT. Subsequently, the correction algorithm was applied. Simulation parameters were: \(\tau=55.6\mu s\), \(N=256\) the simulated scan is \(.917s\).

Results/Discussion

Fig. 3b shows the reconstructed images. RF gradient imaging with linear fields yielded no distortions, whereas imaging with nonlinear fields did. Distortions increased in severity in regions with increasing nonlinearity. These distortions can be corrected according to our method (Fig. 3c, d). Like in the case of standard MRI, distortion correction cannot account for the variable spatial resolution and signal-to-noise ratio that arises when encoding spatial information with nonlinear gradients.

Conclusion

In this study, we demonstrate that, by using a map of the RF gradient, it is feasible to correct image distortions that arise from RF gradient nonlinearity. Simulated reconstructions showed that distortion severity increased in regions with increasing nonlinearity, but that these can be corrected by our method. This approach addresses one of the barriers to the practical use of a transmitted B₁ gradient, like that produced by a surface coil, for spatial encoding in MRI.

Acknowledgements

Schott Family Foundation, the Minnesota Lions, NIH grants P41 EB027061 and U01 EB025153.