2189
Low-field MR imaging using multiplicative regularization1Delft Institute of Applied Mathematics, Delft University of Technology, Delft, Netherlands, 2Circuits and Systems, Delft University of Technology, Delft, Netherlands
Synopsis
We present an image reconstruction approach that incorporates regularization by multiplying the data-fidelity term by a total variation functional. Usually, regularization is carried out in an additive manner, with a regularization parameter balancing out the two terms. Such a parameter often needs to be tuned for each dataset through extensive numerical experimentation. Our approach does not require such a parameter. We applied the method to in-vivo data acquired using a low-field MR scanner. Our results show that the method successfully denoises low-field MR images.
Introduction
Inexpensive, portable low-field MRI scanners are of great clinical relevance. In [1] and [2], among others, it was shown that image reconstruction using such a scanner is possible. Due to weaker static magnetic fields, the SNR in low-field MR scanners is lower than in commercial high-field scanners, yielding relatively noisy images. Many regularization methods exist that effectively remove noise from images. These methods minimize a linear combination of the data-consistency term and some regularizing expression, requiring an artificial regularization parameter, which usually needs to be tuned through extensive numerical experimentation for each new dataset. On the other hand, when multiplicative regularization is used, the data-consistency term is multiplied by a regularizing functional, thereby eliminating the need of a regularization parameter that attempts to balance the two terms. Initially, multiplicative regularization was applied successfully in the field of wave field inversion [3] and we extended it to low-field MRI in [4]. In [4], the method was successfully applied to 3D datasets of fruit. Here, we solve the multiplicatively regularized optimization problem for data acquired from an in vivo knee scan.Methods
We define the data-consistency term as$$F^{\text{data}}(\mathbf{x}) = \frac{\| \mathbf{b} - \mathcal{F}\mathbf{x} \|_{2}^{2}}{\| \mathbf{b} \|_2^2},$$
where, at every iteration, $$$\mathbf{b}$$$ is the k-space data, $$$\mathcal{F}$$$ is the Fourier Transform in 3D and $$$\mathbf{x}$$$ is the desired image. Given an approximation $$$\mathbf{x}_{k-1}$$$ of the image, we minimize the objective function $$F_{k-1}(\mathbf{x}) = F^{\text{data}}(\mathbf{x}) F^{\text{TV}}_{k-1}(\mathbf{x}),$$ where $$$F^{\text{data}}$$$ is the data-consistency term and $$$F^{\text{TV}}_{k-1}$$$ is a multiplicative weighted L2 total variation functional given by $$F_{k-1}^{\text{TV}}(\mathbf{x}) = \int \frac{|\nabla \mathbf{x}|^2 + \delta_{k-1}^2}{|\nabla \mathbf{x}_{k-1}|^2 + \delta_{k-1}^2} \, \text{d}V,$$ with $$$\delta_{k-1}^2 = F^{\text{data}}(\mathbf{x}_{k-1})^2\int |\nabla \mathbf{x}_{k-1}|^2 \, \text{d}V.$$$ We use Polak-Ribière nonlinear conjugate gradient update directions to solve the minimization problem and after each step, $$$F^{\text{TV}}_{k-1}$$$ is updated. As our initial guess, we take a masked version of the inverse FFT of the k-space data.
Results
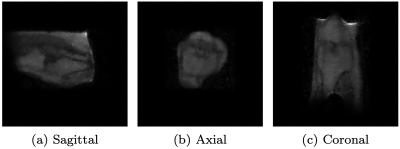
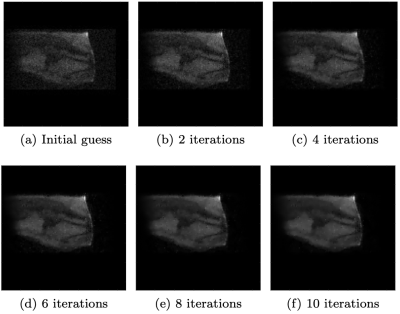
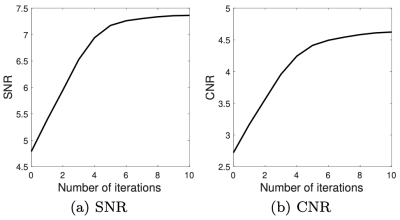
Experimental data was acquired from the knee of a healthy volunteer using the low-field scanner described in [5]. The acquisition parameters of the turbo spin echo sequence were as follows: ETL 9, TR 250 ms, TE 15 ms, number of complex data points 128x128x128, FoV 256x256x256 mm3, pulse duration 100 $$$\mu$$$s, acquisition bandwidth 20 kHz, number of averages 1. Figure 1 shows a sagittal, axial and coronal slice of the noisy 3D image obtained by applying an inverse FFT to the k-space data. Additionally, we solved the multiplicatively regularized minimization problem for this dataset. After 10 iterations, which was when the SNR and CNR values were maximized, the results shown in Figure 2 were obtained. Figure 3 shows the reconstructions for different iteration numbers. We observe that the algorithm progressively denoises the image, which is consistent with the SNR and CNR values that increase as a function of the iteration number, as shown in Figure 4.Discussion
We have seen that, instead of adding a regularization term to the data-consistency term as is usually done in MR image reconstruction, multiplying by a weighted L2 total variation functional also yields reconstructions in which noise is suppressed. Such a multiplicative approach eliminates the need to tune a regularization parameter, which can significantly reduce reconstruction times, since this tuning usually requires extensive numerical experimentation. As the algorithm progresses, noise is increasingly suppressed and it can be terminated as soon as the reconstructions meet a user-specified quality criterion, such as SNR. The method has been successfully applied to a wide variety of three-dimensional low-field datasets and distortions in the gradients and the static background field of the MR scanner can be taken into account as well [4]. Presently, the method is implemented for single-coil data only and future work will therefore focus on extending multiplicative regularization to multi-coil MR measurements. Datasets acquired in compressed sensing experiments will be investigated as well and future work will also include a study of the semi-convergence properties of the method.Conclusion
Our results show that multiplicative regularization can be applied to effectively denoise low-field MR images.Acknowledgements
This research is supported by NWO-WOTRO (Netherlands Organization for Scientific Research) under grant W07.303.101 and by the TU Delft | Global Initiative, a program of the Delft University of Technology to boost Science and Technology for Global Development. The authors would like to thank Tom O'Reilly for carrying out the experiments and Prof. Andrew Webb for sharing his expertise.References
[1] Cooley, C. Z., Stockmann, J. P., Armstrong, B. D., Sarracanie, M., Lev, M. H., Rosen, M. S., & Wald, L. L. (2015). Two‐dimensional imaging in a lightweight portable MRI scanner without gradient coils. Magnetic resonance in medicine, 73(2), 872-883.
[2] O'Reilly, T., Teeuwisse, W. M., & Webb, A. G. (2019). Three-dimensional MRI in a homogenous 27 cm diameter bore Halbach array magnet. Journal of Magnetic Resonance, 307, 106578.
[3] van den Berg, P. M., Abubakar, A., & Fokkema, J. T. (2003). Multiplicative regularization for contrast profile inversion. Radio Science, 38(2).
[4] de Leeuw den Bouter, M.L., van Gijzen, M.B., & Remis, R.F. Low-field magnetic resonance imaging using multiplicative regularization. Magnetic Resonance Imaging, 75, 21-33.
[5] O’Reilly, T., Teeuwisse, W. M., de Gans, D., Koolstra, K., & Webb,
A. G. (2020). In vivo 3D brain and extremity MRI at 50 mT using a
permanent magnet Halbach array. Magnetic Resonance in Medicine, 85(1), 495-505.