2173
Rapid learning of tissue parameter maps through random FLASH contrast synthesis
Divya Varadarajan1,2, Katie Bouman3, Bruce Fischl*1,2,4, and Adrian Dalca*1,5
1Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States, 3Department of Computing and Mathematical Sciences, California Institute of Technology, Pasadena, CA, United States, 4Massachusetts General Hospital, Boston, MA, United States, 5Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States
1Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States, 3Department of Computing and Mathematical Sciences, California Institute of Technology, Pasadena, CA, United States, 4Massachusetts General Hospital, Boston, MA, United States, 5Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States
Synopsis
Estimating tissue properties and synthesizing contrasts can ease the need for long acquisitions and have many clinical applications. In this work we propose an unsupervised deep-learning strategy that employs the FLASH MRI model. The method jointly estimates the T1, T2* and PD tissue parameter maps with the goal to synthesize physically plausible FLASH signals. Our approach is additionally trained for random acquisition parameters and generalizes across different acquisition protocols and provides improved performance over fixed acquisition based training methods. We also demonstrate the robustness of our approach by performing these estimation with as low as three input contrast images.
Introduction
Acquiring multiple MRI images is time consuming. As a result, estimation of tissue parameters (e.g., T1, T2, T2*, proton density (PD)) is commonly performed from a set of acquired scans to enable synthesis of contrasts without prohibitive acquisition time [1-3]. Synthesized contrasts have been used for clinical applications [4], distortion correction [5] and artifact correction [6]. Recent supervised and semi-supervised machine learning based methods [7-9] have shown improved accuracy compared to classical dictionaries [3,10] or constrained optimization methods [11] for estimating tissue parameters from MRI. However, existing work requires prior knowledge of the tissue parameters and models learned only for a specific set of acquisition parameters thus reducing the generalizability of the approach.In this work we propose an unsupervised deep-learning strategy that employs the FLASH MRI model. The method jointly estimates the T1, T2* and PD tissue parameter maps that enable it to synthesize physically plausible FLASH signals for arbitrary scan parameters (consisting of echo time (TE), repetition time (TR) and flip angle (FA)). The proposed strategy involves a network that takes as input images generated from random acquisition parameters and is optimized to be able to reproduce arbitrary contrasts, making it robust to estimations from diverse acquisition protocols with as few as three image contrast inputs.
Method
We propose a neural network that takes in arbitrary FLASH MRI contrasts and estimates the tissue parameters (Fig. 1). Our loss function uses the tissue parameters to synthesize a set of FLASH contrasts (that may be different from the input) and compares them to ground truth data.Let $$$c(p,v)$$$ represent the FLASH forward MRI model (see equation in Fig. 1) for tissue parameters $$$p$$$ (i.e. $$$T_1$$$ , $$$T_2^*$$$, PD) and scan parameters $$$v$$$ (i.e. TE, TR, FA). We assume we have a dataset $$$D$$$ consisting of tissue parameters $$$p$$$. We optimize a 2D convolutional neural network $$$f(\cdot)$$$ which takes in a small number of FLASH MRI contrasts $$$c(p,v_i)$$$, with $$$v_i$$$ scan parameters and $$$p\in D$$$, and outputs an estimate of the tissue parameters $$$\hat(p)$$$. We optimize the unsupervised loss for $$$v_o$$$ scan parameters that we want to synthesize using mean squared error over synthesized contrasts:
$$
L(\theta;D) = \sum_{\{p\in D\}}E_{\{v_i\in T,v_o \in T\}}||c(\hat{p}, v_o)-c(p, v_o)||_2^2\text{, where }\hat{p}=f(c(p, v_i))
$$
where $$$v_i$$$ and $$$v_o$$$ are the scan parameters of the scans used as input and those in the loss, respectively, $$$E$$$ is the expectation operator and $$$T$$$ is the space of scan parameters. Using different scan parameters between the network inputs and the loss helps the network to generalize beyond training input.
Dataset. To demonstrate the proposed network, we obtain a training dataset by estimating $$$T_1$$$, $$$T_2^*$$$ and PD independently using a least squares fitting method [1] from 3-flip, 4-echo FLASH MRI data acquired at 1 mm resolution for 22 ex vivo human brain specimens. We sample scan parameters $$$v_i$$$ and $$$v_o$$$ from a uniform distribution within a preset range and use a FLASH forward model that takes these scan parameters along with tissue parameters to generate three FLASH MRI contrasts. These are given as input to the network.
Evaluation
We compare the proposed approach with a network trained on a fixed acquisition scheme and a loss operating on the input data itself, i.e. $$$v_i =v_o$$$ that are predetermined rather than sampled randomly [8]. We separate 20% of the ex vivo datasets as held-out test data. We compute the mean squared error (MSE) and mean absolute error (MAE) metrics for 100 test slices to evaluate (1) synthesis performance of the two approaches, (2) accuracy of recovered tissue parameter maps and (3) robustness of each approach to perturbations in input scan parameters.Results
Fig 2a. and b. shows that our method achieves lower than the baseline, which was trained using acquisition parameters of a one-flip (FA=20 degrees), 3-echo( [7,15,25] ms) FLASH MRI sequence (TR=37 ms). The proposed method is consistently either comparable or better and importantly exhibits very little variance in the reconstruction error. The baseline reconstruction in 2c. for this example has errors and a large bias, while the proposed method is a much closer match to the reference.Fig 3. compares the parameter map accuracy for the case from Fig. 2. Our network results in lower error mean and variance for all three tissue parameters compared to the baseline, which estimates T1 incorrectly for the example images since the $$$v_i$$$ does not vary in flip angle.
Fig. 4. demonstrates the generalizability of our approach to perturbations in the input acquisition parameter $$$v_i$$$. We randomly perturbed the flip angle up to $$$\pm 10 degrees$$$ , TE up to $$$\pm 7 ms$$$ and TR up to $$$\pm 10 ms$$$ and estimated scans with fixed parameter $$$v_o$$$={TR=37ms, TE = [7 15 25] ms, FA = 20 degrees]} (which the baseline was trained with). Our proposed method yields better results for all 300 different testing configurations.
Conclusion
We demonstrate a new FLASH model based unsupervised learning method that can synthesize arbitrary contrasts with as few as three input contrasts and is generalizable to other acquisitions, and able to synthesize contrasts and estimate parameters using one-fourth the amount of data.Acknowledgements
No acknowledgement found.References
[1] Fischl, B, Salat, D.H, van der Kouwe, A.J.W, Makris, N, Ségonne, F, Quinn, B.T., Dale, A.M.,Sequence-independent segmentation of magnetic resonance images, NeuroImage 2004, Volume 23, Supplement 1, S69-S84, https://doi.org/10.1016/j.neuroimage.2004.07.016.[2] Deoni, S.C.L., Peters, T.M. and Rutt, B.K. (2005), High‐resolution T1 and T2 mapping of the brain in a clinically acceptable time with DESPOT1 and DESPOT2. Magn. Reson. Med., 53: 237-241. https://doi.org/10.1002/mrm.20314
[3] Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495(7440):187-192. doi:10.1038/nature11971
[4] Andica C, Hagiwara A. , et al, Review of synthetic MRI in pediatric brains: Basic principle of MR quantification, its features, clinical applications, and limitations, Journal of Neuroradiology, 2019, 46, Issue 4, , 268-275
[5] Varadarajan, D., Frost, R., van der Kouwe, A., Morgan, L., Diamond, B., Boyd, E., Fogarty, M., Stevens, A., Fischl, B., and Polimeni, J.R., “Edge-preserving B0 inhomogeneity distortion correction for high resolution ultra-high field multiecho ex vivo MRI”, International Society for Magnetic Resonance in Medicine, 2020, p. 664.
[6] Boudreau M, Tardif CL, Stikov N, Sled JG, Lee W, Pike GB. B1 mapping for bias-correction in quantitative T1 imaging of the brain at 3T using standard pulse sequences. J Magn Reson Imaging. 2017 Dec;46(6):1673-1682. doi: 10.1002/jmri.25692. Epub 2017 Mar 16. PMID: 28301086.
[7] Feng L, Ma D, Liu F. Rapid MR relaxometry using deep learning: An overview of current techniques and emerging trends. NMR Biomed. 2020 Oct 15:e4416. doi: 10.1002/nbm.4416. Epub ahead of print. PMID: 33063400.
[8] Liu F, Feng L, Kijowski R. MANTIS: Model-Augmented Neural neTwork with Incoherent k-space Sampling for efficient MR parameter mapping. Magn Reson Med. 2019 Jul;82(1):174-188. doi: 10.1002/mrm.27707. Epub 2019 Mar 12. PMID: 30860285; PMCID: PMC7144418.
[9] Fang Z, Chen Y, Liu M, et al. Deep learning for fast and spatially constrained tissue quantification from highly accelerated data in magnetic resonance fingerprinting. IEEE Trans Med Imaging. 2019;38:2364-2374. https://doi.org/10.1109/TMI.2019.2899328
[10] Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn Reson Med. 2018;79:83-96. https://doi.org/10.1002/mrm.26639
Figures
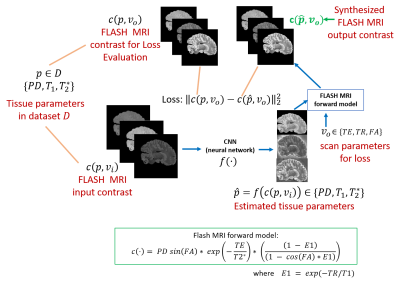
Figure 1: Proposed
framework: The proposed model to synthesize arbitrary FLASH MRI contrasts using
a CNN and a FLASH forward model from three input image contrasts. As a
consequence of using the FLASH model, the output of the CNN can be interpreted
as estimates of the tissue parameters (T1,T2* and PD).

Figure
2: Contrast Synthesis: Test error in synthesis of image contrasts estimated
from three input images over 100 test datasets.
The boxplots in 2a and 2b, plot
the MAE and the images in 2c. show the reference, proposed estimate and
fixed acq. network estimate. The images in 2c. show a slice from the
test dataset, with the reference estimated from 3 flip 4 echo scan and
predicted contrast from both random and fixed networks.
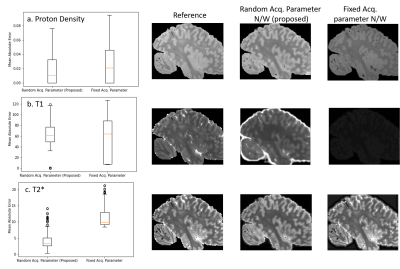
Figure
3: Tissue Parameter Estimation: Test error in tissue parameter maps estimated
from three input images over 100 test datasets. Fixed acq. parameter n/w mis
calculates T1 in the images because the scan contains one flip angle which is
insufficient to characterize T1.
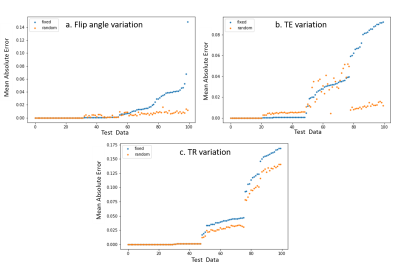
Figure
4: Scan Parameter Robustness. Test Error in synthesis with input acquisition
parameter () variation. MAE is used to
calculate synthesis error. The proposed network is more robust to input
variation due to training with random parameters.