2164
Rapid MR Parametric Mapping using Deep Learning1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
Synopsis
Existing deep learning-based methods for rapid MR parametric mapping often use the reference parametric maps fitted from fully sampled images to train the networks. Nevertheless, the fitted parametric map is sensitive to the noise and the fitting algorithms. In this work, we proposed to incorporate the quantitative physical model into the deep learning framework to simultaneously reconstruct the parameter-weighted images and generate the parametric map without the reference parametric maps. Experimental results on the quantitative MR T1ρ mapping show the promising performance of the proposed framework.
Introduction
Quantitative MR imaging suffers from a long imaging time since multiply parametric-weighted images with varying imaging parameters must be acquired to calculate the parametric map, which significantly hinders their widespread use in clinical applications 1, 2. An alternative way to reduce the scan time of parametric mapping is to undersample in k-space. And prior information is required to generate the parametric map from undersampled k-space data3-9 In this work, we proposed a novel deep learning (DL)-based framework to reconstruct parameter-weighted images and generate the parametric map simultaneously from undersampled k-space data. The experimental results on T1ρ mapping show that the proposed framework achieves superior reconstruction and mapping performance.Theory
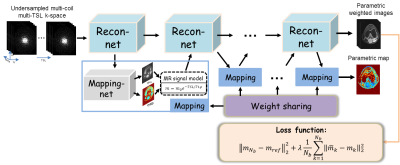
Among various methods for fast parametric mapping, the interaction approach in which the prior information encoded in the physical model is incorporated into the reconstruction of parameter-weighted images exhibits good performance. With deep networks, we proposed to simultaneously reconstruct the parameter-weighted images and the corresponding parametric map, where the whole procedure can be formulated as follows:$$ \begin{cases}m_{n+1}= \Gamma(m_n,\widetilde{m}_n,A^{H}f)\\(M_0,T_x)_{n+1}=U(m_{n+1}) \\\widetilde{m}_{n+1}=S(M_0,T_x)_{n+1}\end{cases} (1)$$ where $$$n$$$ is the iteration number, $$$m$$$ is the $$$T_x$$$ -weighted images from deep reconstruction $$$\Gamma$$$, $$$(M_0,T_x)$$$ is the baseline image and associated $$$T_x$$$ map which are generated simultaneously from network $$$U$$$, $$$\\widetilde{m}$$$ is the synthetic $$$T_x$$$-weighted images satisfying the $$$T_x$$$ signal decay.Take T1ρ mapping for example, Figure 1 represents an overview of the proposed framework. There are two chained networks corresponding to the two task in Eq. (1): reconstruction task $$$\Gamma$$$ (Recon-net) and Mapping task $$$U$$$ (Mapping-net). The physical model was incorporated after Mapping-net to generate T1ρ-weighted images, which then used as one of the inputs of the next Recon-net. The weights in Mapping-net were shared across the iterations. And the loss function was defined as $$||m_{N_b}-m_{ref}||_2^2+\lambda\frac{1}{N_b}\sum_{k=1}^{N_b}||\widetilde{m}_k-m_k||_2^2 (2)$$ where $$$N_b$$$ is the number of blocks referring to the iterations of Eq. (1), $$$m_{ref}$$$ is the reference images from the fully sampled k-space data. $$$\lambda$$$ is the weighting parameter. The second term in loss function enforces the output of the Mapping task the same as input, which provides self-supervised learning for parametric map generation and no need for the reference parametric map.
Method
In this study, the PD-net architecture10 was modified for deep parameter-weighted image reconstruction, and the U-net architecture11 was adopted for generating a parametric map. The number of blocks was set to be 5, and the parameter $$$\lambda$$$ was 0.1.Six healthy volunteers were recruited for T1ρ scanning (4 used for training and the rest for testing), and informed consent was obtained from the imaging object in compliance with the IRB policy. All MR scans were performed on a 3T scanner (uMR 790, United Imaging Healthcare, Shanghai, China) using a commercial 12-channel phased-array knee coil. T1ρ-weighted images of the knee were acquired using a 3D MATRIX sequence and a self-compensated paired spin-lock preparation pulse. 4 training and one testing subjects were with the following imaging parameters: TE/TR = 8.96/2000 ms, matrix size: 256 × 144 × 124, TSLs = 5, 10, 20, 40, and 60 ms. Another testing subject was scanned with TE/TR = 65.8/1000 ms, matrix size: 192 × 172 × 100, TSLs = 5, 10, 20, 40, and 55 ms.
The fully sampled data was retrospectively undersampled using Poisson-disk masks with accelerations of 7.6 and 9.2. The coil sensitivity maps were calculated from the fully-filled k-space center using ESPIRiT12.
Results
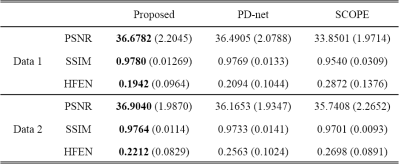
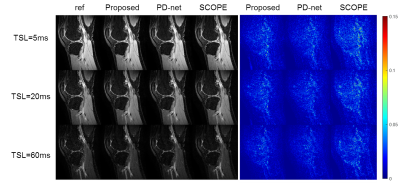
We compared the proposed approach with the state-of-the-art parametric mapping method SCOPE9 and a two-step DL-based method PD-net+mapping. The quantitative and qualitative comparison results are shown in Table I and Figure 2. It can be seen that the DL-based methods can achieve better reconstruction performance than conventional non-DL method.Figure 3 shows the reconstruction of Data 1 at R=7.6. The selected ROI of T1ρ map is overlaid on the reconstructed T1ρ.-weighted image at TSL=5ms The ROI T1ρ mean values and standard deviations of the different methods are provided below the images. The proposed approach gives the most similar values of T1ρ to the reference.
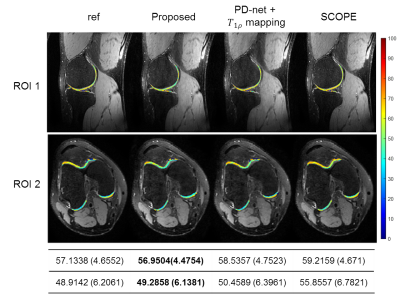
Figure 4 demonstrates the overlaid reconstructions of Data 2 at R=9.2 with different methods. It can be seen from the mean and standard deviation values of the T1ρ map of ROI that the proposed approach shows good agreement with reference in T1ρ map estimation.
Conclusion
In this work, we proposed an efficient DL-based framework that can reconstruct parametric-weighted images and generate the parameter map simultaneously. Results on in vivo T1ρ knee imaging exhibit the superior performance of the proposed approach. The extension to other types of parametric mapping and more properties will be explored in the future.Acknowledgements
This work was supported partly by the National Natural Science Foundation of China (61771463, 81830056, U1805261, 81971611, 61871373, 81729003, 81901736); National Key R&D Program of China (2017YFC0108802 and 2017YFC0112903); Natural Science Foundation of Guangdong Province (2018A0303130132); Shenzhen Peacock Plan Team Program (KQTD20180413181834876); Innovation and Technology Commission of the government of Hong Kong SAR (MRP/001/18X); Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000).References
[1] Duvvuri U, Charagundla S, Kudchodkar S, et al. Human knee: in vivo T1(rho)-weighted MR imaging at 1.5 T—preliminary experience. Radiology 2001, 220(3):822-6.
[2] Regatte R, Akella S, Lonner J, et al. T1rho relaxation mapping in human osteoarthritis (OA) cartilage: comparison of T1rho with T2. J Magn Reson Imaging 2006, 23(4):547-53.
[3] Block K, Uecker M, Frahm J. Model-Based Iterative Reconstruction for Radial Fast Spin-Echo MRI. IEEE Trans Med Imaging 2009, 28(11):1759-1769.
[4] Sumpf T, Uecker M, Boretius S, et al. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imaging 2011, 34(2):420-428.
[5] Welsh C, Dibella E, Adluru G, et al. Model-based reconstruction of undersampled diffusion tensor k-space data. Magn Reson Med 2013, 70(2):429-440.
[6] Tran-Gia J, Stab D, Wech T, et al. Model-based Acceleration of Parameter mapping (MAP) for saturation prepared radially acquired data. Magn Reson Med 2013, 70(6):1524-34.
[7] Zhu Y, Peng X, Wu Y, et al. Direct diffusion tensor estimation using a model-based method with spatial and parametric constraints. Medical Physics 2017, 44(2):570-580.
[8] Peng X, Ying L, Liu Y, et al. Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA). Magn Reson Med 2016, 76(6):1865-1878.
[9] Zhu Y, Liu Y, Ying L, et al. SCOPE: signal compensation for low-rank plus sparse matrix decomposition for fast parameter mapping. Phys Med Biol 2018, 63(18):85009.
[10] Cheng J, Wang H, Ying L, Liang D. Model Learning: Primal Dual Networks for Fast MR Imaging. MICCAI 2019
[11] Ronneberger O, Fischer P, Brox T. U‐Net: convolutional networks for biomedical image segmentation. MICCAI 2015
[12] Uecker M, et al. ESPIRiT-An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE Meets GRAPPA. Magn Reson Med 2014, 71(3):990-1001.
Figures