2084
Automatic and robust background phase correction on phase-contrast MRI using M-estimate SAmple Consensus (MSAC)1Magnetic Resonance, Siemens Healthcare GmbH, Erlangen, Germany, 2Physikalisch-Technische-Bundesanstalt (PTB), Braunschweig and Berlin, Germany, 3Department of Medical Imaging, Technical University of Berlin, Berlin, Germany, 4School of Imaging Sciences and Biomedical Engineering, King's College London, London, United Kingdom
Synopsis
Background phase correction is necessary to correctly quantify flow velocity values from 2D phase-contrast MR images. However, typically used static tissue correction is susceptible to wrap-around resulting in even larger quantification errors. In this work, we successfully implemented a robust and automatic background phase correction algorithm based on M-estimate Sample Consensus (MSAC). MSAC achieves robust results over wide ranges of its few parameters. Based on 49 phase-contrast time series with and without wrap-around, MSAC reduced the average root-mean-squared error from 1.71±0.34cm/s (static fit correction) to 0.78±0.07cm/s (MSAC) in presence of wrap-around.
Introduction
Phase-contrast (PC) MRI remains a valuable tool for flow velocity assessment and derived hemodynamic parameters. Full clinical acceptance of 2D PC-MRI remains hampered by velocity offsets, mainly generated by eddy currents, propagating into clinically unacceptable errors in derived integrated values such as stroke volumes or retrograde flow fractions1.Correction methods include (1) phantom correction (correction values from static phantom scan with identical protocol) which is difficult in a routine setting or (2) static tissue fit correction of nth-order polynomials2, which fails in cases of insufficient static tissue and/or wrap-around artifacts3. Regularized weighted-least-square fits were introduced4 to increase fit-stability and recently an outlier detection algorithm to discard wrap-around was proposed3.
We introduce a correction approach based on M-estimate SAmple Consensus5 (MSAC), designed for robust fitting in presence of outliers (e.g. pixels affected by wrap-around). MSAC has only few parameters, is fast and is easy to implement.
In this abstract, we prove feasibility and compare MSAC to static tissue fit corrections and phantom corrections as a gold standard.
Materials and Methods
Acquisition:Data from seven volunteers and from a static phantom were acquired on 1.5T and 3T clinical MRI systems (MAGNETOM Sola/Vida, Siemens Healthcare, Erlangen, Germany) using multi-channel body and spine coil arrays.
2D PC-MRI measurements were performed to quantify flow in the ascending aorta (AAo), the main pulmonary artery (MPA) and in the left and right pulmonary arteries (LPA/RPA) using a retrospectively gated breath-held through-plane velocity-encoded spoiled gradient-echo sequence with varying degrees of wrap-around (Figure 1a). Phantom measurements were acquired using the same protocols following each volunteer measurement.
Correction:
For static tissue fit and for MSAC correction, a magnitude mask using a temporally averaged magnitude image was created to filter noise and pre-select pixels of interest in the temporally averaged phase image (pixel pool M). MSAC randomly selects m samples from M and fits the polynomial surface to these samples. Outliers are selected based on the absolute distance $$$\epsilon$$$ of pixels in the pool M and on the fitted surface. Pixels below a threshold t build a consensus set. This selection and fitting process is repeated N-times (Figure 1b).
After all iterations, the consensus set Cn with lowest cost $$C_{n}=\sum_{i\in\mathrm{M}}\begin{cases}{\epsilon}_i&{\epsilon}_i<t\\{t}&{\epsilon}_i\geq{t}\end{cases}$$ is selected and all included pixels then used for the final background fit.
An analysis of MSAC parameters and fit orders was performed.
If not otherwise stated, MSAC parameters were set to N=1000, m=10 and t=0.01*venc. MSAC pixel-selection was based on a 1st-order polynomial followed by a 2nd-order polynomial background fit correction.
MSAC was compared to phantom correction and 2nd-order static tissue fit correction2.
Evaluation:
The background offsets were subtracted from each timeframe. For each acquisition, fit quality was assessed by the root-mean-squared error of pixels p in a specified region of interest (ROI): $$\mathrm{RMSE}=\sqrt{{\small\frac{1}{\mathrm{N}_{\mathrm{ROI}}}}\sum_{i\in\mathrm{ROI}}(p_i-p_{i,Phantom})^2}$$
Additionally, flow volumes (Q) were compared.
ROIs were segmented using Segment6. Computations were performed in Matlab7.
Results
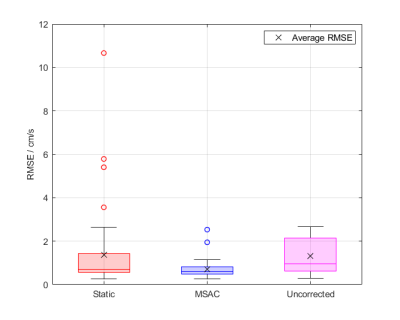
Figure 2 illustrates masks generated by MSAC and static fit correction in AAo and MPA images with wrap-around. MSAC-corrected quantification results are comparable to the phantom correction while the static correction leads to larger errors than uncorrected values.This holds true for a range of MSAC parameters (Figure 3), showing robustness for larger ranges of sample size m and iterations N. MSAC performance is reduced for very low and very high threshold values.
Fit order dependency is depicted in Figure 4, showing RMSE for different outlier detection orders and correction orders. MSAC performs best with 0th- and 1st-order detection.
Figure 5 shows a direct comparison of MSAC to static tissue correction over all acquisitions. MSAC achieves an average RMSE of $$${\small{0.78\pm0.07\mathrm{cm/s}}}$$$ and $$${\small{0.51\pm0.03\mathrm{cm/s}}}$$$ in presence and without wrap-around respectively, static correction achieves $$${\small{1.71\pm0.34\mathrm{cm/s}}}$$$ and $$${\small{0.63\pm0.08\mathrm{cm/s}}}$$$ and uncorrected average background errors are $$${\small{1.26\pm0.13\mathrm{cm/s}}}$$$ and $$${\small{1.50\pm0.22\mathrm{cm/s}}}$$$, respectively.
MSAC-correction required $$${\small{11\pm1\mathrm{s}}}$$$ per time-resolved dataset.
Discussion
RMSE comparisons in ROIs show that MSAC achieves similar results to static tissue in wrap-around-free images and is superior in presence of wrap-around. MSAC fit-stability is expected to be reduced for higher degrees of wrap-around due to reduced pixel availability but remains superior due to outlier rejection (Figure 2, Figure 5).MSAC mainly depends on the threshold parameter (Figure 3). Large thresholds interfere with outlier detection, leading to unrestricted masks, low thresholds are too sensitive, reducing pixel density and influencing fit-stability. However, MSACs independency to varying number of trials and to sample sizes make it a robust algorithm without the need of a thorough parameter optimization.
MSAC depends on the fit order chosen for the outlier rejection algorithm. Higher-order fits have more parameters that are fit to a fixed sample size, which are not necessarily well-distributed across the image, thus leading to more variability in the consensus set (Figure 4).
Conclusion
We showed, that MSAC is superior to static fit correction, especially if wrap-around is present. Further investigation is needed to compare MSAC to other, more sophisticated methods3,4.Future work will analyze MSACs stability to a wider acquisition parameter space and as an on-line correction method in a clinical routine setting. An application to 4D Flow is also warranted.
In conclusion, we showed that MSAC outperforms the static correction on a limited number of datasets with and without wrap-around.
Acknowledgements
No acknowledgement found.References
1. Gatehouse, P., Rolf, M., Graves, M., Hofman, M., Totman, J., Werner, B., Quest, R., Liu, Y., Von Spiczak, J., Dieringer, M., Firmin, D., Van Rossum, A., Lombardi, M., Schwitter, J., Schulz-Menger, J., & Kilner, P. (2010). Flow measurement by cardiovascular magnetic resonance: A multi-centre multi-vendor study of background phase offset errors that can compromise the accuracy of derived regurgitant or shunt flow measurements. Journal of Cardiovascular Magnetic Resonance, 12(1), 1–8. https://doi.org/10.1186/1532-429X-12-5
2. Walker, P. G., Cranney, G. B., Scheidegger, M. B., Waseleski, G., Pohost, G. M., & Yoganathan, A. P. (1993). Semiautomated method for noise reduction and background phase error correction in MR phase velocity data. Journal of Magnetic Resonance Imaging, 3(3), 51–530. https://doi.org/10.1002/jmri.1880030315
3. Pruitt, A. A., Jin, N., Liu, Y., Simonetti, O. P., & Ahmad, R. (2019). A method to correct background phase offset for phase-contrast MRI in the presence of steady flow and spatial wrap-around artifact. Magnetic Resonance in Medicine, 81(4), 2424–2438. https://doi.org/10.1002/mrm.27572
4. Ebbers, T., Haraldsson, H., Dyverfeldt, P., Sigfridsson, A., Warntjes, M., & Wigström, L. (2008). Higher order weighted least-squares phase offset correction for improved accuracy in phase-contrast MRI. Proc. Intl. Soc. Mag. Reson. Med., 1367.
5. Torr, P. H. S., & Zisserman, A. (2000). MLESAC: A new robust estimator with application to estimating image geometry. Computer Vision and Image Understanding, 78(1), 138–156. https://doi.org/10.1006/cviu.1999.0832
6. Heiberg, E., Sjögren, J., Ugander, M., Carlsson, M., Engblom, H., & Arheden, H. (2010). Design and validation of Segment - freely available software for cardiovascular image analysis. BMC Medical Imaging, 10(1), 1. https://doi.org/10.1186/1471-2342-10-1
7. The MathWorks, Inc. (2018). Matlab (Version R2019b) [Computer Software]. https://mathworks.com/
Figures
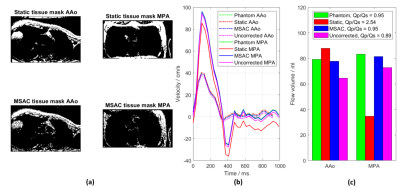


Figure 4: Comparison of correction fit order (0th-, 1st-, 2nd- and 3rd-order polynomials, colors) versus MSAC-mask detection fit order (0th-, 1st-, 2nd- and 3rd-order polynomials, MSAC 0-3) from two volunteers. The RMSE and the standard deviation of the mean over all corrections is given for each combination. It shows that fit-quality is best for low-order MSAC detection. Static fit correction worsens for higher-order polynomials.