2034
Scanning post mortem fixed whole human brain for advanced higher order diffusion modelling using a 300 mT/m whole-body MRI scanner1Department of Neurophysics, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany, 2Center for Cognitive Neuroscience Berlin, Freie Universität Berlin, Berlin, Germany, 3Paul Flechsig Institute of Brain Research, Leipzig University, Leipzig, Germany, 4Institute of Neuroscience and Medicine, Research Centre Jülich, Jülich, Germany, 5C. and O. Vogt Institute for Brain Research, Heinrich Heine University Düsseldorf, Düsseldorf, Germany, 6Felix Bloch Institute for Solid State Physics, Leipzig University, Leipzig, Germany
Synopsis
Higher order diffusion modelling (diffusional kurtosis and multi-tissue CSD) of a whole post mortem human brain with excellent tissue quality was enabled by ultra-high b values from a whole-body 3T scanner with ultra-strong gradients. This was complemented by a novel gradient nonlinearity correction scheme to interpolate signals onto diffusion shells before estimation of fibre distributions. The brain is part of the BigBrain initiative, and will undergo an extensive atlasing procedure. This dataset will thus extend the studies possible on the future BigBrain atlas, allowing investigation into diffusion microstructure imaging and tractography.
Introduction
Diffusion imaging of post mortem human brain can be used to validate diffusion models and tractography, as the tissue can afterwards undergo histological processing to investigate the biological substrates of the model parameters and fibre tracts1.However, diffusion imaging of post mortem tissue is challenging because of reduced diffusivity relative to in vivo, making measurement of in vivo-equivalent protocols over volumes with whole brain coverage difficult, especially since post mortem and fixation-driven relaxivity increases require short diffusion encodings1,2. The larger post mortem delay in human investigations compared to that possible in animal experiments exacerbates these problems1.
Recently-developed whole-body scanners with ultra-strong gradients3 can be used to probe post mortem brains at the needed high diffusion weightings with short diffusion encodings4,5. Here, we show that such scanners allow high diffusion weighting protocols sufficient for higher-order diffusion modelling in post mortem whole human brain. The effects of gradient nonlinearity6 (GNL) on the diffusion encoding are mitigated by acquiring an extra shell per nominal shell to allow interpolation onto a single shell.
Further, the scanned brain is part of the BigBrain initiative7 and thus has exceptional tissue quality. It will undergo an extensive histological atlasing procedure8, allowing for validation of higher order diffusion models and tractography.
Methods
A post-mortem human brain (female, age of death: 73yrs, cause of death: acute respiratory syndrome, post-mortem time before fixation: 7h, fixation time: 4 months). Tissue acquisition, handling, and fixation were as described previously7. The brain was transferred to phosphate buffered solution (PBS, pH 7.4) 72h before scanning to remove formaldehyde monomers (which reduce T22) from the tissue. For MRI scanning, the brain was placed in a custom-made head-shaped container filled with degassed PBS, and exposed to 1 mBar vacuum for 12h to remove air bubbles.The brain was scanned on a Siemens 3T Connectom system using a 32ch receive-only head coil. The diffusion protocol was adapted from Veraart, et al.9: interleaved $$$b=6,30$$$ ms/µm$$$^2$$$ with 120 and 240 non-colinear diffusion directions, respectively, distributed over the whole sphere; 2.5 mm isotropic resolution with whole-brain coverage; spin-echo EPI sequence3; multiband10 2; GRAPPA11 2 ; TE 66 ms; TR 3500 ms; Gmax 273 mT/m; acquisition time 24 minutes. The whole protocol was repeated with $$$b=9,10,19,20,29$$$ ms/µm$$$^2$$$. This gave a multishell protocol for kurtosis imaging12, and pairs $$$b=(9,10),(19,20),(29,30)$$$ to allow $$$b$$$ interpolation (see below). The $$$b$$$ are approximately $$$10\times$$$ in vivo values13 to account for reduced ex vivo diffusivity2. For susceptibility correction, 10 $$$b=0$$$ images with opposed phase encoding were acquired.
Data were denoised14,15, and corrected for susceptibility, motion, and eddy current artefacts16,17,18 using MRtrix319. GNL geometric distortions (but not diffusion encodings) were corrected using HCP tools20. From the geometric correction, voxelwise gradient deviations $$$L$$$ were computed for diffusion encoding correction6,21 (see below). Diffusion kurtosis maps12 were fitted using the MDT toolbox22.
The normalised signal with diffusion encoding vector $$$\vec{q}$$$ is: $$s(L\vec{q},b)=\langle\exp\{-b(\vec{q}^TL^TD_\Omega{}L\vec{q})\}\rangle_\Omega,$$ where $$$D_\Omega$$$ denotes the diffusion tensor of element $$$\Omega$$$ of the spin-ensemble in a voxel, and $$$\langle\cdot\rangle_\Omega$$$ an average over the ensemble. First-order cumulant expansion23 around $$$b|L\vec{q}|^2=b_0$$$ gives $$s(L\vec{q},b)\approx{}s(\vec{q}_0,b_0)\exp\left\{-(b|L\vec{q}|^2-b_0)d(\vec{q}_0,b_0)\right\}$$ where $$$\vec{q}_0=L\vec{q}/|L\vec{q}|,$$$ $$s(\vec{q}_0,b_0)=\langle\exp\{-b_0\vec{q}_0^TD_\Omega\vec{q}_0\}\rangle_\Omega,$$ and the pseudo-diffusion coefficient $$d(\vec{q}_0,b_0)=s(\vec{q}_0,b_0)^{-1}\vec{q}_0^T\left\langle\exp\{-b_0\vec{q}_0^TD_\Omega\vec{q}_0\}D_\Omega\right\rangle_\Omega\vec{q}_0.$$ Based on these relations, signals were interpolated to the average of pairs of shells over the whole brain using log-linear fitting in Matlab. Previous methods24,25 have made a tensor expansion around $$$b=0$$$, however that only retains angular resolution up to 4th-order26. Our method retains the angular resolution of the data.
MRtrix3 was used to calculate fibre orientation distribution functions (fODFs) and tissue segmentations using multi-tissue constrained spherical deconvolution (MT-CSD)19,27. To evaluate the GNL correction, calculations were performed on both the original data and the interpolated data.
Results
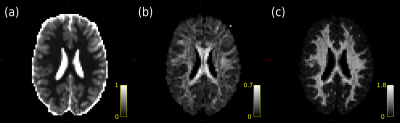
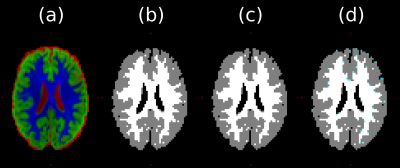
Fig. 1 shows diffusional kurtosis maps computed from the data. The mean MD over the WM segmentation in Fig. 2b is 0.13 µm$$$^2$$$/ms, compared to $$$\approx1$$$ µm$$$^2$$$/ms in vivo, confirming that our $$$b$$$ selection is appropriate for kurtosis fitting compared to in vivo13.Figs. 2 and 3 show that MT-CSD gives reasonable results, and that the GNL correction gives slight improvements.
Discussion
Our protocol avoids problems of bSSFP28 and stimulated echo29 based methods, which have ill-defined $$$b$$$. It also requires no sequence changes, unlike segmented-EPI based methods30, and is significantly faster (hours of scanning, not days), minimising interference with the histology pipeline7. The resolution is coarse compared to previous approaches4,28,29,30, but allows ultra-high $$$b$$$.The voxelwise effects of accounting for GNL in fODF estimation are small, however small effects can significantly affect tractography and comparison measures25. Limitations of the MT-CSD algorithm mean voxelwise changes in gradient direction could not be included in the estimation, and so residual angular errors will remain. This could be mitigated by pseudo-diffusion tensors, which would interpolate signals on the sphere.
Conclusion
The high maximum $$$b$$$ from the ultra-strong diffusion gradients, and excellent tissue quality allowed characterisation of diffusional kurtosis, to our knowledge for the first time, in whole human post mortem brain. This was complemented by a novel GNL correction scheme to interpolate signals onto diffusion shells before estimation of fibre distributions. This dataset will extend the studies possible on the future BigBrain atlas, allowing investigation into diffusion microstructure imaging and tractography.Acknowledgements
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement no. 616905. This project has received funding from the BMBF (01EW1711A & B) in the framework of ERA-NET NEURON. This project has received funding from the European Union's Horizon 2020 Framework Programme for Research and Innovation under the Specific Grant Agreement No. 945539 (Human Brain Project SGA3). We thank Jelle Veraart and Erika Raven for providing the axon diameter mapping protocol.References
[1] Roebroeck, A, Miller, KL, Aggarwal, M. (2019), "Ex vivo diffusion MRI of the human brain: Technical challenges and recent advances", NMR Biomed. https://doi.org/10.1002/nbm.3941
[2] Shepherd, T.M., Thelwall, P.E., Stanisz, G.J. and Blackband, S.J. (2009), "Aldehyde fixative solutions alter the water relaxation and diffusion properties of nervous tissue", Magn. Reson. Med. https://doi.org/10.1002/mrm.21977
[3] Setsompop, K., Kimmlingen, R., Eberlein, E., Witzel, T., Cohen-Adad, J., McNab, J.A., Keil, B., Tisdall, M.D., Hoecht, P., Dietz, P., Cauley, S.F., Tountcheva, V., Matschl, V., Lenz, V.H., Heberlein, K., Potthast, A., Thein, H., Van Horn, J., Toga, A., Schmitt, F., Lehne, D., Rosen, B.R., Wedeen, V., Wald, L.L. (2013), "Pushing the limits of in vivo diffusion MRI for the Human Connectome Project", Neuroimage. https://doi.org/10.1016/j.neuroimage.2013.05.078
[4] McNab, J.A., Edlow, B.L., Witzel, T., Huang, S.Y., Bhat, H., Heberlein, K., Feiweier, T., Liu, K., Keil, B., Cohen-Adad, J., Tisdall, M.D., Folkerth, R.D., Kinney, H.C., Wald, L.L. (2013), "The Human Connectome Project and beyond: Initial applications of 300mT/m gradients", Neuroimage. https://doi.org/10.1016/j.neuroimage.2013.05.074
[5] Jones, D.K., Alexander, D.C., Bowtell, R., Cercignani, M., Dell'Acqua, F., McHugh, D.J., Miller, K.L., Palombo, M., Parker, G.J.M., Rudrapatna, U.S., Tax, C.M.W. (2018), "Microstructural imaging of the human brain with a `super-scanner': 10 key advantages of ultra-strong gradients for diffusion MRI", Neuroimage. https://doi.org/10.1016/j.neuroimage.2018.05.047
[6] Bammer, R., Markl, M., Barnett, A., Acar, B., Alley, M., Pelc, N., Glover, G. and Moseley, M. (2003), "Analysis and generalized correction of the effect of spatial gradient field distortions in diffusion‐weighted imaging", Magn. Reson. Med. https://doi.org/10.1002/mrm.10545
[7] Amunts, K., Lepage, C., Borgeat, L., Mohlberg, H., Dickscheid, T., Rousseau, M.-É., Bludau, S., Bazin, P.-L., Lewis, L.B., Oros-Peusquens, A.-M., Shah, N.J., Lippert, T., Zilles, K., Evans, A.C. (2013), "BigBrain: An Ultrahigh-Resolution 3D Human Brain Model", Science. https://doi.org/10.1126/science.1235381
[8] Amunts, K., Mohlberg, H., Bludau, S., Zilles, K., (2020), "Julich-Brain: A 3D probabilistic atlas of the human brain's cytoarchitecture", Science. https://doi.org/10.1126/science.abb4588
[9] Veraart, J., Raven, E.P., Edwards, L.J., Weiskopf, N., Jones, D.K. (under revision), "The variability of MR axon radii estimates in the human brain". https://doi.org/10.21203/rs.3.rs-104158/v1
[10] Setsompop, K., Cohen-Adad, J., Gagoski, B.A., Raij, T., Yendiki, A., Keil, B., Wedeen, V.J., Wald, L.L. (2012), "Improving diffusion MRI using simultaneous multi-slice echo planar imaging", Neuroimage. https://doi.org/10.1016/j.neuroimage.2012.06.033
[11] Griswold, M.A., Jakob, P.M., Heidemann, R.M., Nittka, M., Jellus, V., Wang, J., Kiefer, B. and Haase, A. (2002), "Generalized autocalibrating partially parallel acquisitions (GRAPPA)", Magn. Reson. Med. https://doi.org/10.1002/mrm.10171
[12] Jensen, J.H., Helpern, J.A., Ramani, A., Lu, H. and Kaczynski, K. (2005), "Diffusional kurtosis imaging: The quantification of non‐gaussian water diffusion by means of magnetic resonance imaging", Magn. Reson. Med. https://doi.org/10.1002/mrm.20508
[13] Chuhutin, A., Hansen, B., Jespersen, S.N. (2017), "Precision and accuracy of diffusion kurtosis estimation and the influence of b‐value selection". NMR in Biomedicine. https://doi.org/10.1002/nbm.3777
[14] Veraart, J., Novikov, D.S., Christiaens, D., Ades-aron, B., Sijbers, J., Fieremans, E. (2016), "Denoising of diffusion MRI using random matrix theory", Neuroimage. https://doi.org/10.1016/j.neuroimage.2016.08.016
[15] Cordero-Grande, L., Christiaens, D., Hutter, J., Price, A.N., Hajnal, J.V., (2019) "Complex diffusion-weighted image estimation via matrix recovery under general noise models", Neuroimage. https://doi.org/10.1016/j.neuroimage.2019.06.039
[16] Andersson, J. L. Skare, S., Ashburner, J. (2003), "How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging", Neuroimage. https://doi.org/10.1016/S1053-8119(03)00336-7
[17] Smith, S.M., Jenkinson, M., Woolrich, M.W., Beckmann, C.F., Behrens, T.E., Johansen-Berg, H., Bannister, P.R., De Luca, M., Drobnjak, I., Flitney, D.E., Niazy, R.K., Saunders, J., Vickers, J., Zhang, Y., De Stefano, N., Brady, J.M., Matthews, P.M. "Advances in functional and structural MR image analysis and implementation as FSL", Neuroimage. https://doi.org/10.1016/j.neuroimage.2004.07.051
[18] Andersson, J. L., Sotiropoulos, S. N. (2016), "An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging", Neuroimage. https://doi.org/10.1016/j.neuroimage.2015.10.019
[19] Tournier, J.D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T., Pietsch, M., Christiaens, D., Jeurissen, B., Yeh, C.-H., Connelly, A. (2019) "MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation", Neuroimage. https://doi.org/10.1016/j.neuroimage.2019.116137
[20] Glasser, M.F., Sotiropoulos, S.N., Wilson, J.A., Coalson, T.S., Fischl, B., Andersson, J.L., Xu, J., Jbabdi, S., Webster, M., Polimeni, J.R., Van Essen, D.C., Jenkinson, M. (2013), "The minimal preprocessing pipelines for the Human Connectome Project", Neuroimage. https://doi.org/10.1016/j.neuroimage.2013.04.127
[21] Sotiropoulos, S.N., Jbabdi, S., Xu, J., Andersson, J.L., Moeller, S., Auerbach, E.J., Glasser, M.F., Hernandez, M., Sapiro, G., Jenkinson, M., Feinberg, D.A., Yacoub, E., Lenglet, C., Van Essen, D.C., Ugurbil, K., Behrens, T.E.J. (2013), "Advances in diffusion MRI acquisition and processing in the Human Connectome Project", Neuroimage. https://doi.org/10.1016/j.neuroimage.2013.05.057
[22] Harms, R.L., Fritz, F.J., Tobisch, A., Goebel, R., Roebroeck, A. (2017) "Robust and fast nonlinear optimization of diffusion MRI microstructure models", Neuroimage. https://doi.org/10.1016/j.neuroimage.2017.04.064
[23] Kiselev, V.G. and Il'yasov, K.A. (2007), "Is the "biexponential diffusion" biexponential?", Magn. Reson. Med. https://doi.org/10.1002/mrm.21164
[24] Paquette, M., Eichner, C., Anwander. A. (2019), "Gradient non-linearity correction for spherical mean diffusion imaging". Proceedings of the 27th Annual Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM).
[25] Mesri, H.Y., David, S., Viergever, M.A., Leemans, A. (2020), "The adverse effect of gradient nonlinearities on diffusion MRI: From voxels to group studies", Neuroimage. https://doi.org/10.1016/j.neuroimage.2019.116127
[26] Novikov, D.S., Veraart, J., Jelescu, I.O., Fieremans, E. (2018), "Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI", Neuroimage. https://doi.org/10.1016/j.neuroimage.2018.03.006
[27] Jeurissen, B., Tournier, J.-D., Dhollander, T., Connelly, A., Sijbers, J. (2014), "Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data", Neuroimage. https://doi.org/10.1016/j.neuroimage.2014.07.061
[28] Foxley, S., Jbabdi, S., Clare, S., Lam, W., Ansorge, O., Douaud, G., Miller, K. (2014), "Improving diffusion-weighted imaging of post-mortem human brains: SSFP at 7T", Neuroimage. https://doi.org/10.1016/j.neuroimage.2014.08.014
[29] Fritz, F.J., Sengupta, S., Harms, R.L., Tse, D.H., Poser, B.A., Roebroeck, A. (2019), "Ultra-high resolution and multi-shell diffusion MRI of intact ex vivo human brains using kT-dSTEAM at 9.4T", Neuroimage. https://doi.org/10.1016/j.neuroimage.2019.116087
[30] Miller, K.L., Stagg, C.J., Douaud, G., Jbabdi, S., Smith, S.M., Behrens, T.E.J., Jenkinson, M., Chance, S.A., Esiri, M.M., Voets, N.L., Jenkinson, N., Aziz, T.Z., Turner, M.R., Johansen-Berg, H., McNab, J.A., "Diffusion imaging of whole, post-mortem human brains on a clinical MRI scanner" (2011), Neuroimage. https://doi.org/10.1016/j.neuroimage.2011.03.070
Figures