2033

Analysis of high-resolution 3T diffusion MRI data obtained with minimal CUSP acquisition scheme from a Non-Human Primate

Alex Colin Valcourt Caron¹, Amir Shmuel², Ilana R. Leppert², and Maxime Descoteaux¹
¹Université de Sherbrooke, Sherbrooke, QC, Canada, ²Montreal Neurological Institute, McGill University, Montreal, QC, Canada

Synopsis

The validation of advanced diffusion MRI methods requires acquisition at high-resolution and high SNR, which is difficult to obtain in humans. The use of anesthetized Non-Human Primates (NHPs) is key to unlocking valid microstructural maps. However, data acquisition and analysis tools must be adapted and configured for successful application to NHPs imaging. Here we propose a processing pipeline allowing for the analysis of diffusion data using DTI, CSD, and DIAMOND reconstruction, tailored for the analysis of data from the macaque brain. We present results obtained by applying the pipeline to a dataset acquired with a minimal CUSP 90 directions scheme.

Introduction

The study of diffusion-based connectivity in the human brain has improved greatly across the past decade. However, a great deal of validation work needs to be done on advanced methods. For this purpose, the use of in-vivo Non-Human Primates (NHPs), whose brain structure is closely similar to the human brain, is crucial. NHPs can be imaged under anesthesia, making it possible to avoid head movement and obtain large amounts of data images acquired at high spatial and angular resolution¹. Here, we present a processing pipeline for analyzing diffusion MRI data obtained from the macaque monkey brain, using datasets acquired at a resolution of 0.8 mm and an optimized CUSP² scheme with 90 directions. These data made it possible to accurately reconstruct the microstructural maps and orientational information.

Methods

Experimental design. We applied a Stejskal-Tanner sequence on a 3T Siemens MAGNETOM Prisma, with 80 mT/m maximum gradient strength, and an 8 channels head coil. The diffusion data was acquired using an optimized 90 directions CUSP² scheme at a nominal b-value 3000 s/mm²with 12 b0 volumes interleaved (TE=71 ms, TR=4.5 s, GRAPPA/3, SMS/2, GSLIDER/5, 4 mm slice thickness, partial Fourier 6/8), in the AP and PA PE directions, with 0.8 mm isotropic voxels. B1+ maps were acquired to correct for the B1 field inhomogeneities. Structural T1 images were acquired, with 0.53 mm isotropic voxels (MPRAGE-PAT, TE=3.3 ms, TR=2.4 s, GRAPPA/2).

Preprocessing. The diffusion volumes were first denoised using MP-PCA decomposition^3,4,5,6. The multiple repetitions of acquired T1w images and the diffusion images obtained with the 2 PE directions were then co-registered (rigid + affine transformations) using ANTs⁷ to the mean b0 image. Next, the T1 volumes were denoised using Non-Linear Means. The diffusion data was further corrected for phase distortions using Topup^8,9 applied to the b0 groups of AP and PA directions, and for motion and susceptibility artifacts using Eddy^10,11,12 on the complete AP>>PA set. All images were then normalized using the N4 bias field correction¹³, and upsampled to 0.4 mm isotropic voxels. Finally, The T1 images was registered (rigid + affine + syn) to their corresponding mean b0 diffusion volume using ANTs.

Reconstruction and analysis. Diffusion tensors fit (DTI¹⁴), fiber ODFs through constrained spherical deconvolution (CSD¹⁵), and multivariate gamma distribution tensor fit (DIAMOND¹⁶) were computed. Diffusion measures (MD, AD, RD, FA) as well as the mode, norm and principal direction were extracted from the DTI. The principal directions, NuFO and AFD were computed from the fODFs. We estimated the classical diffusion measures from the multi-tensor fit weighted by fascicles, as well as various indices of average and variance of diffusion.

Results

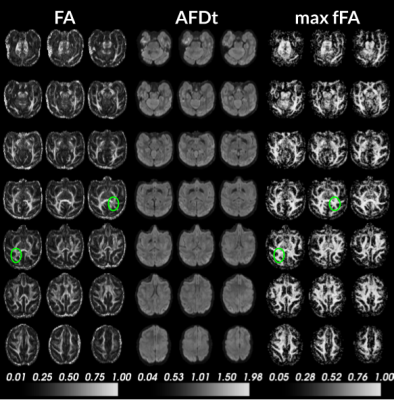
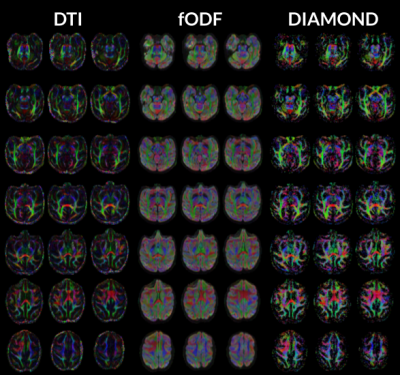
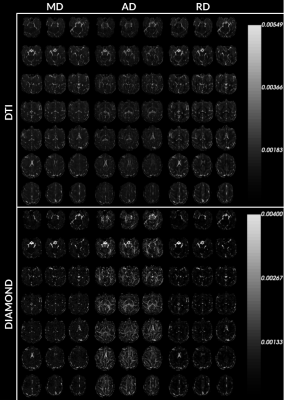
Figure 1 and 2 display anisotropy measures obtained from the DTI, fOFD and DIAMOND fit. They show the capacities of the two latter methods at separating the effects of microstructure from those of the underlying geometry.

Figure 3 presents the diffusion measurements obtained from DTI compared to DIAMOND. For the latter, the measures were averaged from the fascicles, weighted by their estimated fraction. The increased contrast between white matter, grey matter and CSF in AD and RD measures demonstrates a clear advantage of the DIAMOND reconstruction.

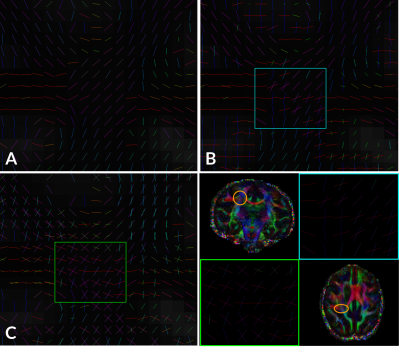
Figure 4 presents the orientations obtained in the right posterior region of the centrum semiovale, at a crossing of the CC, projections from the CST and SLF. It displays two-way crossings between CC and CST obtained from the fODF. The multi-tensor fit extracted a greater portion of the two-way and three-way crossing in the region.

Conclusion

Using a CUSP acquisition scheme with a small number of directions (90), we demonstrate the recovery of white matter microstructural features and orientational information from high-resolution diffusion data of the macaque brain. Moreover, we show that estimating those measures with a high-dimensional model (e.g., DIAMOND) is possible with the minimal number of acquired directions.

Acknowledgements

The authors would like to thank the grants from the FRQS Quebec Bioimaging Network and McGill University CF-REF Healthy Brains, Healthy Lives Fund awarded to Dr. Amir Shmuel, the NSERC Discovery grant held by Pr Descoteaux and the Université de Sherbrooke institutional chair in neuroinformatics.

References

1. Glasser M, Smith S, Marcus D et al. The Human Connectome Project's neuroimaging approach. Nat Neurosci. 2016;19:1175–1187. https://doi.org/10.1038/nn.4361

2. Scherrer B, Warfield SK. Parametric representation of multiple white matter fascicles from cube and sphere diffusion MRI. PLoS One. 2012;7(11):e48232. doi: 10.1371/journal.pone.0048232.

3. Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. NeuroImage. 2016;142:394-406. doi: 10.1016/j.neuroimage.2016.08.016

4. Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn. Res. Med. 2016;76(5):1582-1593. doi: 10.1002/mrm.26059

5. Cordero-Grande L, Christiaens D, Hutter J, Price AN, Hajnal JV. Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage. 2019;200:391-404. doi: 10.1016/j.neuroimage.2019.06.039

6. Tournier J-D, Smith RE, Raffelt D, Tabbara R, Dhollander T, Pietsch M, Christiaens D, Jeurissen B, Yeh C-H, Connelly A. MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. NeuroImage. 2019:202;116137. doi: 10.1016/j.neuroimage.2019.116137

7. Avants BB, Tustison NJ, Wu J, Cook PA, Gee JC. An open source multivariate framework for n-tissue segmentation with evaluation on public data. Neuroinformatics. 2011 Dec;9(4):381-400. doi: 10.1007/s12021-011-9109-y

8. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003;20(2):870-888. doi: 10.1016/S1053-8119(03)00336-7

9. Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy R, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23(S1):208-219. doi: 10.1016/j.neuroimage.2004.07.051

10. Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2016;125:1063-1078. doi: 10.1016/j.neuroimage.2015.10.019

11. Andersson JLR, Graham MS, Zsoldos E, Sotiropoulos SN. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. NeuroImage. 2016;141:556-572. doi: 10.1016/j.neuroimage.2016.06.058

12. Andersson JLR, Graham MS, Drobnjak I, Zhang H, Filippini N, Bastiani M. Towards a comprehensive framework for movement and distortion correction of diffusion MR images: Within volume movement. NeuroImage. 2017;152:450-466. doi: 10.1016/j.neuroimage.2017.02.085

13. Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC. N4ITK: improved N3 bias correction. IEEE transactions on medical imaging. 2010;29(6):1310–1320. doi: 10.1109/TMI.2010.2046908

14. Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H. Diffusion tensor imaging: concepts and applications. J Magn Reson Imaging. 2001 Apr;13(4):534-46. doi: 10.1002/jmri.1076

15. Tournier J-D, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. NeuroImage. 2007;35(4):1459-1472. doi: 10.1016/j.neuroimage.2007.02.016

16. Scherrer B, Schwartzman A, Taquet M, Sahin M, Prabhu SP, Warfield SK. Characterizing brain tissue by assessment of the distribution of anisotropic microstructural environments in diffusion-compartment imaging (DIAMOND). Magn Reson Med. 2016 Sep;76(3):963-77. doi: 10.1002/mrm.25912

Figures

Anisotropy measurements obtained from DTI (FA), fODF (AFDt) and DIAMOND (max fFA). Green circles indicate regions where the single tensor FA failed to delineate microstructural anisotropy of multiple fascicles, which results in a drop of intensity, but are recovered with max fFA. As expected, AFDt presents a higher density of fibers in the grey matter, as can be observed by the higher contrasts in the cortical band.

RGB maps from the multiple reconstruction methods. Note the higher contrasts present in the DIAMOND map, from which the effect of free water is removed, leading to higher intensities of the underlying FA, and thus higher contrasts.

Typical tensor measures compared to their counterparts from DIAMOND, where the effect of multi-tensor fit can be observed. It isolates the free water compartment from the fascicles representing the underlying white matter, resulting in higher contrast in tensor diffusivity measures, particularly in AD and RD, where white matter voxels are distinctly contrasted from the surrounding grey matter.

Peaks extracted from (A) DTI, (B) fODF, and (C) DIAMOND. Whereas DTI cannot reconstruct the multi-peak populations, two-way crossings were successfully extracted from both fODF and DIAMOND. The latter presents a greater number of crossings.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

2033