2007
Relaxation corrected simulated MM model for improved fitting and quantification of 1H FID MRSI data1Max Planck Institute for Biological Cybernetics, Tübingen, Germany, 2IMPRS for Cognitive and Systems Neuroscience, Tübingen, Germany, 3University of Tübingen, Faculty of Science, Tübingen, Germany, 4Advanced Imaging Research Center, UT Southwestern Medical Center, Dallas, TX, United States
Synopsis
Short TE MRS and very short TR (TR < 300) MRSI are popular methods to capture snapshots of the neurochemical profile; however, these popular methods suffer from strong influence from underlaying macromolecular signals. This work shows a simulation method developed at 9.4T and extendable to other field strengths to account for macromolecule signals. The method developed is compared to three more commonly used methods of accounting for macromolecule signals. Results show improved metabolite mapping by use of simulated macromolecule basis vectors.
Introduction
MRSI adds valuable diagnostic information to understanding pathologies such as multiple sclerosis1, tumors2, epilepsy3 and neurodegenerative diseases4,5 due to detectable variations of the neurochemical profile. High-resolution 1H-FID MRSI of the human brain has been showcased previously at 3T6, 7T7, and 9.4T8, and displayed promise in detecting a more comprehensive neurochemical profile compared to results relying on longer TE methods and/or lower field strengths9.However, acquiring high-resolution 1H FID MRSI data with sufficient coverage of the brain in a time efficient manner requires a very short TR of < 300ms which leads to substantial T1-weighting of metabolites7,10 and macromolecules11 (MMs). To accurately quantify 1H-FID MRSI data and to derive reliable metabolite maps, an accurate MM basis is needed as input for spectral fitting. However, it is practically impossible to experimentally acquire a matching MM basis set as is routinely done for short TE single voxel spectroscopy12 due to short TRs and SAR constraints of respective inversion recovery sequences.
Few studies have attempted to account for the MM spectrum in short TR MRSI data13–15. This study seeks to improve quantification precision of 1H-FID MRSI data and the quality of metabolite maps by introducing a relaxation corrected simulated MM model and cross-validating it against three more commonly used methods to account for MM signals.
Methods
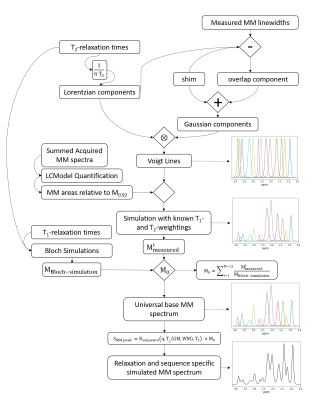
This work uses a MM simulation model16 to account for underlying MM signals. Figure 1 shows the algorithm developed to simulated MM signals. The algorithm simulates Voigt lines and combines knowledge of T1- and T2-relaxation times in combination with single-spin Bloch simulations to create relaxation specific MM basis vectors.Three healthy volunteers participated in this study with IRB approval and signed consent. An 18/32 Tx/Rx coil17 was utilized to acquire high-resolution 1H-FID-MRSI (TE* = 1.5ms, TR = 300ms) with a matrix size of 64x64 (nominal voxel size: 3.44x3.44x8mm3), flip angle of 47°, BW of 4000Hz, and 512 data points acquired. Water references with identical sequence parameters were acquired to account for bias fields caused by the receive coil and to correct for coil loading between volunteers. All MRSI data were acquired from a slice positioned directly above the corpus callosum for each volunteer. Previous 9.4T results have shown the benefits of additional T1-correction of the metabolite signals in FID MRSI18, which was also applied herein.
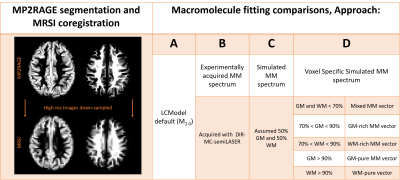
MP2RAGE data was acquired and reconstructed as described in Hagberg et al.19 and segmented using SPM1220. The tissue type composition was then extracted from each voxel and MRSI data was preprocessed as described by Wright et al.18 Spectral fitting was performed in LCModel (v-6.3)21 using a FID-sequence basis set created using VeSPA22.
All basis sets contained identical metabolite vectors. However, the MM components were altered with four approaches (Figure 2).
Results
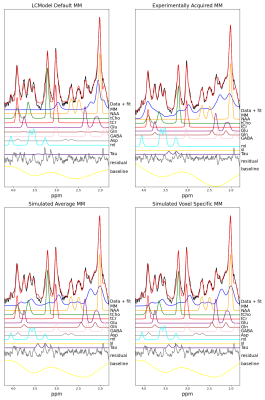
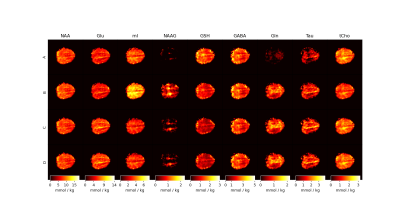
Figure 3 displays the fit from a pure WM voxel with four different MM baseline approaches.As can be seen in metabolite maps (Figure 4), an Approach B did not perform well and severely impacted the quality of mI and NAAG maps. It can be seen that Approaches A, C, and D are relatively similar with resulting metabolite concentration differences that are not nearly as strong.
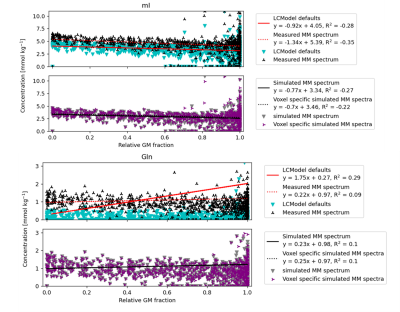
Figure 5 regressions show mI and Gln concentrations against the relative GM fraction. The top compares Approach A and Approach B, and the bottom compares Approach C and Approach D.
Discussion
Figure 2 shows that the MM baseline model varies substantially between the different methods. Approach A failed to account for MM between 3.1-4.1ppm, which potentially leads to overestimation of metabolites from 3.4-4.0ppm.Figure 3 and Figure 4 suggest that Approach B may not be ideal for fitting MRSI data. Furthermore, the Approach A led to a reduction of fitted voxels for NAAG. This could lead to misestimation of other metabolites such as NAA, Glu, Gln, and GABA which overlap with M2.0 in various degrees. As seen in Figure 3 and Figure 4, Gln is not fitted when using Approach A.
Figure 5 shows that the general trend of metabolites between WM and GM is relatively similar independent of the MM approach used. However, the intercept of approach A and B tend to vary with metabolites having resonances around 2ppm and 3.6ppm. This implies that the MM approaches are seriously affecting the quality of fit for the metabolites in those regions. It does not appear to matter much which simulated MM approach is used for fitting as the results are fairly similar, but it is clear that the simulated MM spectra perform overall better.
Based on Figure 3, Figure 4, and Figure 5 it is evident that the LCModel settings and experimental baselines both fail to capture different portions of the neurochemical profile. Thus, using a simulated MM spectrum is likely the best avenue to achieve accurate, quantitative metabolite mapping in the human brain.
Conclusion
This work investigated quantitative 1H-FID MRSI with various methods to account for the underlaying MM spectrum. In our findings using an experimental MM spectrum or the LCModel default simulation model is not appropriate for MRSI data, while using a relaxation corrected simulated MM baseline is likely the best option. However, there was not a strong difference between using Approach C or Approach D.Acknowledgements
This project was co-sponsored by the Horizon 2020 grant / CDS-QUAMRI / 634541, the ERC Starting Grant / SYNAPLAST / 679927, and the Cancer Prevention and Research Institute of Texas (CPRIT) Grant / RR180056References
1. Jain S, Sima DM, Sanaei Nezhad F, et al. Patch-Based Super-Resolution of MR Spectroscopic Images: Application to Multiple Sclerosis. Front Neurosci. 2017;11(January):1-12. doi:10.3389/fnins.2017.00013
2. Li Y, Larson P, Chen AP, et al. Short-echo three-dimensional H-1 MR spectroscopic imaging of patients with glioma at 7 tesla for characterization of differences in metabolite levels. J Magn Reson Imaging. 2015;41(5):1332-1341. doi:10.1002/jmri.24672
3. Gilliam FG, Maton BM, Martin RC, et al. Hippocampal 1H-MRSI correlates with severity of depression symptoms in temporal lobe epilepsy. Neurology. 2007;68(5):364-368. doi:10.1212/01.wnl.0000252813.86812.81
4. Schreiner SJ, Kirchner T, Wyss M, et al. Low episodic memory performance in cognitively normal elderly subjects is associated with increased posterior cingulate gray matter N-acetylaspartate: a 1H MRSI study at 7 Tesla. Neurobiol Aging. 2016;48:195-203. doi:10.1016/J.NEUROBIOLAGING.2016.08.022
5. Schreiner SJ, Kirchner T, Narkhede A, et al. Brain amyloid burden and cerebrovascular disease are synergistically associated with neurometabolism in cognitively unimpaired older adults. Neurobiol Aging. 2018;63:152-161. doi:10.1016/J.NEUROBIOLAGING.2017.12.004
6. Maudsley AA, Domenig C, Govind V, et al. Mapping of brain metabolite distributions by volumetric proton MR spectroscopic imaging (MRSI). Magn Reson Med. 2009;61(3):548-559. doi:10.1002/mrm.21875
7. Bogner W, Gruber S, Trattnig S, Chmelik M. High-resolution mapping of human brain metabolites by free induction decay 1 H MRSI at 7 T. 2012;(May 2011):873-882. doi:10.1002/nbm.1805
8. Nassirpour S, Chang P, Henning A. High and ultra-high resolution metabolite mapping of the human brain using 1H FID MRSI at 9.4T. Neuroimage. 2016;(July):1-11. doi:10.1016/j.neuroimage.2016.12.065
9. Motyka S, Moser P, Hingerl L, et al. The influence of spatial resolution on the spectral quality and quantification accuracy of whole-brain MRSI at 1.5T, 3T, 7T, and 9.4T. Magn Reson Med. 2019;82(2):551-565. doi:10.1002/mrm.27746
10. Nassirpour S, Chang P, Henning A. High and ultra-high resolution metabolite mapping of the human brain using 1H FID MRSI at 9.4T. Neuroimage. 2016;(July):1-11. doi:10.1016/j.neuroimage.2016.12.065
11. Murali‐Manohar S, Wright AM, Borbath T, Avdievich NI, Henning A. A novel method to measure T 1 ‐relaxation times of macromolecules and quantification of the macromolecular resonances. Magn Reson Med. August 2020:mrm.28484. doi:10.1002/mrm.28484
12. Cudalbu C, Behar KL, Bhattacharyya PK, et al. Contribution of macromolecules to brain 1H MR spectra: Experts’ consensus recommendations. NMR Biomed. 2020. doi:10.1002/nbm.4393
13. Heckova E, Považan M, Strasser B, et al. Effects of different macromolecular models on reproducibility of FID-MRSI at 7T. Magn Reson Med. 2020;83(1):12-21. doi:10.1002/mrm.27922
14. Považan M, Strasser B, Hangel G, et al. Simultaneous mapping of metabolites and individual macromolecular components via ultra-short acquisition delay 1 H MRSI in the brain at 7T. Magn Reson Med. 2017;00:1-10. doi:10.1002/mrm.26778
15. Nassirpour S, Chang P, Henning A. High resolution maps of individual macromolecule components in the human brain at 9.4T. In: The ISMRM 25th Annual Meeting & Exhibition. Honolulu, HI, USA; 2017.
16. Wright A, Murali-Manohar S, Henning A. Relaxation corrected and Sequence-dependent Macromolecule Baseline Model. In: 27th Annu Meet Exhib Int Soc Magn Reson Med (ISMRM 2019). Montréal, QC, Canada; 2019. 17. Avdievich NI, Giapitzakis I-A, Bause J, Shajan G, Scheffler K, Henning A. Double-row 18-loop transceive-32-loop receive tight-fit array provides for whole-brain coverage, high transmit performance, and SNR improvement near the brain center at 9.4T. Magn Reson Med. 2019;81(5):3392-3405. doi:10.1002/mrm.27602
18. Wright A, Murali Manohar S, Henning A. Quantitative Metabolite Mapping of the Human Brain at 9.4 T. 2020:158.
19. Hagberg GE, Bause J, Ethofer T, et al. Whole brain MP2RAGE-based mapping of the longitudinal relaxation time at 9.4T. Neuroimage. 2017;144:203-216. doi:10.1016/j.neuroimage.2016.09.047
20. Ashburner J, Barnes G, Chen C, et al. SPM12 Manual. Wellcome Trust Centre for Neuroimaging, London, UK; 2014.
21. Provencher SW. Automatic quantitation of localizedin vivo1H spectra with LCModel. NMR Biomed. 2001;14(4):260-264. doi:10.1002/nbm.698
22. Soher B. Versatile Simulation Pulses and Analysis. User Code Contributions – semi-LASER. https://scion.duhs.duke.edu/vespa/contrib/wiki/1f03e57e-1d27-4d36-8b31-db9e5e2f73e82013.
Figures