1995
Effect of digitization in gradient modulated adiabatic pulses with a spatial offset.1Magnetic Resonance Spectroscopy Core, NIH, NIMH, Bethesda, MD, United States
Synopsis
Spectroscopy on high field clinical scanners with limited RF amplitude suffer from large chemical shift artifacts with conventional pulses. Latest developments in adiabatic pulses with modulated gradients like GOIA-WURST pulses offer wide bandwidth at low RF amplitude. The modulated gradient however requires spatial offsets to be added to the phase modulation of the RF pulse. The additional phase offset may cause error due to insufficient digitization of the rapidly changing RF phase. We examined this effect on the voxel profile for two popular pulse parameter sets.
Introduction
Current clinical scanners are equipped with multiple channel receive coils to improve SNR and a body coil for transmitting RF. This setup however limits the maximum allowed B1 amplitude at about 640 Hz (15μT) (1). Conventional RF pulses excite the magnetization over the bandwidth of the pulse at the same time, causing the amplitude to be proportional to the bandwidth of the pulse. The limit on B1 amplitude compares unfavorably to the chemical shift in proton spectroscopy, at three Tesla the frequency difference between choline and NAA is 153 Hz and at seven Tesla 257 Hz. This frequency difference leads to a shift in localization, the chemical shift error (CSE), as high as 40%. Recent developments in adiabatic pulses (2, 3) offer a solution for the CSE problem, in these pulses magnetization is excited serially over the bandwidth of the RF pulse, decoupling the maximum B1 amplitude and the bandwidth of the pulse. Furthermore, modulation of the selection gradient lowers the required B1 level even more so that it is possible to have less than five millisecond pulses, with a bandwidth of 10 kHz, and a limited B1 level of 640 Hz (1). However, the technical setup of the scanner and the modulation of the selection gradient requires any spatial offset of the pulse to be added to the pulse waveform as a phase modulation proportional to the modulation of the gradient. The impact of these additional phase steps may require a high degree to digitization to sufficiently characterize the RF phase profile, to properly approximate the analytical equations defining the pulse. To study how this affects the voxel shape we simulated the effect of spatial offsets on two of the popular GOIA-WURST(16,4) adiabatic pulse shapes.Methods
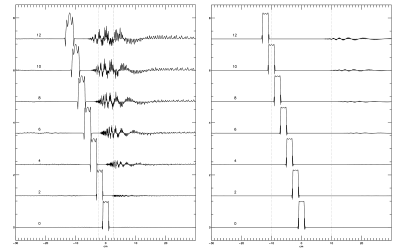
The two GOIA-WURST(16,4) pulse shapes were calculated and simulated in GAMMA (4, 5, 6), an updated GAMMA library was installed from (7). The two sets of RF parameters (number of points, sample interval, bandwidth range, B1 max level, and gradient amplitude modulation factor f) for the pulses were: pulse 1) (175, 20 us, -10 kHz … 10 kHz, 817 Hz, 0.90) from Andronesi (3) for a pulse length of 3.5 ms, and pulse 2) (450, 10 us, -5 kHz … 5 kHz, 640 Hz, 0.85) from Deelchand (1) for the “across vendor standardization” with a pulse length of 4.5 ms. A simple PRESS sequence was used for the simulation with four equally spaced pulses, the first two to select the x dimension and the last two pulses the y dimension. The simulated field of view was chosen large enough to cover the effect of a folded pulse over the Nyquist limit of the RF pulse, 60 * 60 cm in 1024 * 1024 steps. The size of the selected voxel dimension was 2 * 2 cm in the xy plane. The excitation pulse for the z dimension was an ideal 90 degrees pulse. The voxel image was simulated to study the voxel shape for spatial offsets of 2, 4, … 8, 12 cm.Results and Discussion
In figure 1 the point-to-point phase increments in degrees are shown for the two RF pulses, with the Nyquist frequency limit of 180 degrees shown as a dotted line. For appropriate digitization of RF phase the digitization density is expected to be at least several fold higher than that required by the Nyquist limit. The first pulse is just within the Nyquist limits for the unshifted pulse, an offset of only two centimeters puts the pulse over the limit at the end of the pulse. The second pulse is more conservatively dimensioned and exceeds the limit at an offset of 10 cm. Figure 2 shows the resulting voxel profiles for these pulses and their spatial offsets. The voxel profile deteriorates quickly for pulse 1. The more conservatively dimensioned pulse 2 results in much better profiles but the profile deteriorates already at an offset of 6 cm, before the phase modulation of the RF pulse crosses the Nyquist limit as expected from insufficient digitization. Simulations of the two pulses with a sample interval of 1 us show no artifacts for all simulated spatial offsets. This step size is well within the technical specifications of commercial clinical scanners and should be used to avoid contamination of the spectroscopy voxel from outside signals.Acknowledgements
No acknowledgement found.References
(1) Deelchand DK, Berrington A, Noeske R, Joers JM, Arani A, Gillen J, Schär M, Nielsen J-F, Peltier S, Seraji-Bozorgzad N, Landheer K, Juchem C, Soher BJ, Noll DC, Kantarci K, Ratai EM, Mareci TH, Barker PB, Öz G. Across-vendor standardization of semi-LASER for single-voxeMRS at 3T, NMR in Biomedicine. 2019; e4218.
(2) Tannús A, Garwood M. Adiabatic pulses. NMR in Biomedicine, 10 (1997) 423-434.
(3) Andronesi OC, Ramadan S, Ratai EM, Jennings D, Mountford CE, A. Sorensen G. Spectroscopic imaging with improved gradient modulated constant adiabacity pulses on high-field clinical scanners. J. Mag. Reson. 203 (2010) 283-293.
(4) Smith SA, Levante TO, Meier BH, Ernst RR. Computer simulations in Magnetic Resonance; an object oriented programming approach. J Magn Reson 1994; 106a: 75-105.
(5) van der Veen JW, Marenco S, Shen J. Improvements on extraction of glutamate and glutamine from GABA editing spectra at 3 Tesla. Proceedings of the Annual Joint Meeting ISMRM, Milan, Italy, 2014; 2889.
(6) van der Veen JW, van Ormondt D, de Beer R. Simulating metabolite basis sets for in vivo MRS quantitation, incorporating details of the PRESS pulse sequence by means of the GAMMA C++ library. Proceedings ICT OPEN 2012, Rotterdam, the Netherlands, 2012; 40–45.
(7) http://scion.duhs.duke.edu/vespa/gamma
Figures