1981
Kernel-based Fast EPTI Reconstruction with Neural Network
Muheng Li1, Jie Xiang2, Fuyixue Wang3,4, Zijing Dong3,5, and Kui Ying2
1Department of Automation, Tsinghua University, Beijing, China, 2Department of Engineering Phycics, Tsinghua University, Beijing, China, 3A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 4Harvard-MIT Health Sciences and Technology, MIT, Cambridge, MA, United States, 5Department of Electrical Engineering and Computer Science, MIT, Cambridge, MA, United States
1Department of Automation, Tsinghua University, Beijing, China, 2Department of Engineering Phycics, Tsinghua University, Beijing, China, 3A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 4Harvard-MIT Health Sciences and Technology, MIT, Cambridge, MA, United States, 5Department of Electrical Engineering and Computer Science, MIT, Cambridge, MA, United States
Synopsis
A machine learning based reconstruction framework for Echo Planar Time-resolved Imaging(EPTI) is proposed. This work utilized the special data acquisition trajectory of EPTI, a highly-accelerated spatiotemporal CAIPI sampling, to divide the k-space recovery task into a multi-process program. The missing data is filled within an indicated small kernel with a fully connected neural network. Through image reconstruction tests on human brain data set acquired by EPTI, we demonstrated the high efficiency of this algorithm by shortening the reconstruction time of 216×216×48×32 k-data from over 10 minutes to about 20 seconds.
Introduction
Applications of magnetic resonance temperature imaging(MRTI) in real-time temperature monitoring during thermal tumor ablation are promising but challenging, due to slow acquisition of conventional MR sequences. EPTI1, with a highly-accelerated spatiotemporal CAIPI sampling, can efficiently provide multi-contrast images at different echo times(TE), thus becomes an ideal technique for MRTI. However, the reconstruction time restricts its practical application. The recovery of the missing data in EPTI by a GRAPPA-like algorithm is time-consuming2 and not practical for real-time temperature mapping.This work implemented a fast machine learning based image reconstruction algorithm for EPTI. Traditional neural networks are often driven by massive data sets3, but public MRTI data sets are usually insufficient. To overcome the limitation of small data sets, a small amount of calibration data is used as training a neural network. To further accelerate the reconstruction, a kernel-based model is specifically designed for particular EPTI sampling trajectory. By introducing multi-process parallel computing approach on a GPU server, the reconstruction time has been reduced over 30 times, which allows a dynamic temperature imaging during ablation to be feasible.
Methods
Sliding kernel: EPTI performs encoding in ky-t space and uses a new highly accelerated spatiotemporal CAIPI sampling trajectory to take advantage of signal correlation along these dimensions (Fig.1a). Two kernel windows with different sizes are designed to achieve a good trade off between image quality and reconstruction efficiency (Fig.1b). We only recover the missing data in one kernel at a time and then slide the window in the k-space data matrix collected by EPTI until the complete k-space information is restored.Neural network: Fitting the mapping function from the acquired data vector to the target region vector based on fully-sampled calibration scan is important for the reconstruction process (Fig.2). We replace the conventional linear mapping with a neural network, making it robust to non-linear deviation such as magnetic field drift and electronic noise, etc4. The network returns to the basic 1D structure with two fully connected hidden layers(Fig.3). All layers use Leaky ReLU as an activation function. We use Adam as our optimizer, and set learning rate to 0.001 and conduct 2000 iterations. The neural network is implemented in TensorFlow. Missing data of EPTI can be restored by applying this model into the under-sampled ky-t space.
EPTI reconstruction experiments: Data were obtained from Massachusetts General Hospital(MGH) with a Siemens Prisma 3T scanner. Training results with three different loss function (MSE, MAE, Huber) and different number of nodes in each hidden layer were compared. In addition, considering that the calculation within each kernel are independent, we introduced parallel computing so that neural networks can perform operations on multiple kernels simultaneously, further accelerating the data restoration process. The relationship between the reconstruction time and the number of processes were tested to obtain the most effective one.
Results
The corresponding reconstruction results under the three loss functions are not much different. MAE performs a little better in terms of the mean square error of the reconstructed images(Fig.4a). More neural nodes mean more flexibility and higher accuracy but at the cost of longer calculation and problems such as overfitting. The H100-H50 network has already achieved good results (Fig. 4b) with different contrasts (Fig. 4c). Furthermore, because of using different kernel, the computation within each kernel is independent so that the parallel computing becomes workable, further reducing the total reconstruction time from about 130 seconds to 20 seconds (Fig. 5).Conclusion
This work demonstrated the high efficiency of a non-linear EPTI data recovery algorithm with kernel based neural network by shortening the total reconstruction time to less than 20 seconds, 30 times faster than the conventional linear algorithm. Future work will focus on optimization of the network structure and validation of its robustness in real MRTI when heat resource is introduced.Acknowledgements
No acknowledgement found.References
[1] Wang, F., Dong, Z., Reese, T. G., Bilgic, B., Katherine Manhard, M., Chen, J., ... & Setsompop, K. (2019). Echo planar time‐resolved imaging (EPTI). Magnetic resonance in medicine, 81(6), 3599-3615.[2] Griswold, M. A., Jakob, P. M., Heidemann, R. M., Nittka, M., Jellus, V., Wang, J., ... & Haase, A. (2002). Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 47(6), 1202-1210.
[3] Wang, S., Su, Z., Ying, L., Peng, X., Zhu, S., Liang, F., ... & Liang, D. (2016, April). Accelerating magnetic resonance imaging via deep learning. In 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI) (pp. 514-517). IEEE.
[4] Chang, Y., Liang, D., & Ying, L. (2012). Nonlinear GRAPPA: A kernel approach to parallel MRI reconstruction. Magnetic Resonance in Medicine, 68(3), 730-740.
Figures
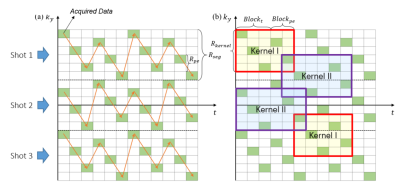
Figure1. Illustration of (a)EPTI acquisition trajectory and (b)reconstruction kernel. The sizes of the two indicated kernel are Blockt+Blockpe and Blockt+Blockpe+1 respectively. Acquired data covers the same matrix points in each kernel, with the top left point always collected.
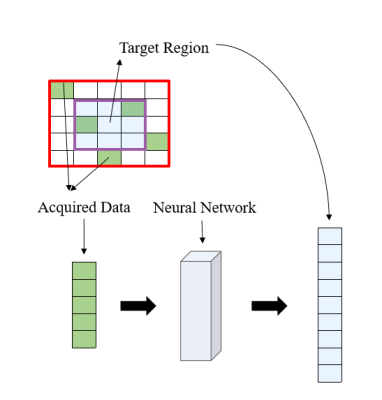
Figure2. Process of restoring the missing k-data in the specified kernel. Extract the acquired data in this kernel and all the data in the target region as a 1D vector respectively. The mapping function can be fitted based on the fully sampled calibration data.
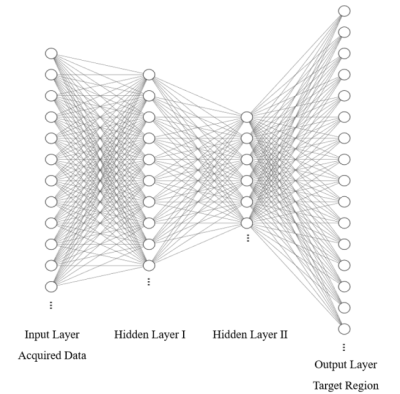
Figure3. Structure of the fully connected neural network with two hidden layers. Leaky ReLU activation function achieves nonlinearity. Real and imaginary part of the complex-valued k-data are input and output in parallel channels of each layer.
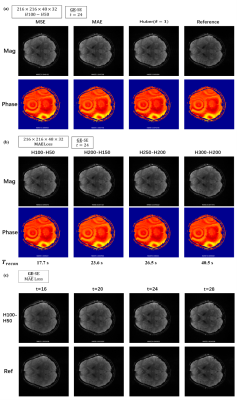
Figure4. Reconstructed images with different (a)loss function: MSE, MAE, Huber (b)number of nodes in each hidden layer (c)multi-contrast and reference images by conventional linear algorithm.
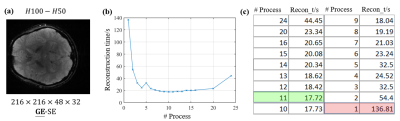
Figure5. (a)Reconstructed image; relationship between the reconstruction time and number of processes shown by (b)dotted line and (c)form.