1980
Compressed sensing MRI via a fusion model based on image and gradient priors
Yuxiang Dai1, Cheng yan Wang2, and He Wang1
1Institute of Science and Technology for Brain-Inspired Intelligence, Fudan University, Shanghai, China, 2Human Phenome Institute, Fudan University, Shanghai, China
1Institute of Science and Technology for Brain-Inspired Intelligence, Fudan University, Shanghai, China, 2Human Phenome Institute, Fudan University, Shanghai, China
Synopsis
Compressed sensing (CS) has been employed to accelerate magnetic resonance imaging (MRI) by sampling fewer measurements. We proposed a fusion model based on the optimization method to integrate the image and gradient-based priors into CS-MRI for better reconstruction results via convolutional neural network models. In addition, the proposed fusion model exhibited effective reconstruction performance in magnetic resonance angiography (MRA).
Introduction
In the past decades, a large variety of optimization algorithms1-6 have been developed to improve CS-MRI reconstruction. However, conventional iterative optimization-based CS-MRI failed to achieve real time reconstructions and became time-consuming due to lots of iterative operations. Meanwhile, these methods need to define appropriate parameters when reconstructing different images with complex structure. Most of deep learning-based CS-MRI merely learnt an end-to-end mapping in pixel domain with large training sets, which may lose the detailed anatomical information of complex images and smoothing the MR images. Additionally, some deep learning methods used in iterative optimizations-based CS-MRI tend to ignore the prior knowledge, which leads to poor performance comparing with the iterative optimization methods. Hence, we developed a novel gradient-based deep network prior for CS-MRI to reduce the above-mentioned impacts of the limitations of iterative optimization and deep learning CS-MRI algorithms.Methods
CNN architectureInstead of training an end-to-end network in pixel domain, the proposed gradient-based deep network priors were integrated into the model-based optimization. To be specific, we proposed the multi-scale dilated network (MDN) to obtain anatomical information in pixel domain (Figure 1). The dilated convolutions were exploited to extend the receptive field of convolutional kernels and extract multi-scale information. The global and local residual learnings were utilized to ensure the abundance of extracted features, and concatenation layers were adopted to make full use of abundant features which can maintain image details. Then images were decomposed into X and Y directions of gradient domain, in which the difference in the pixel values of gradient images was conducive to enhancing the image contrast. With the features reconstruction via single-scale residual learning network (SRLN) shown in Figure 1, the contrast of edges in gradient domain was well enhanced, which is beneficial to the final reconstruction results.
Fusion scheme
As shown in Figure 1, we made an attempt to incorporate CNN priors with model-based optimization for CS-MRI, where the spatial regularization term of model-based optimization scheme was replaced with CNN priors composed of enhanced gradient images. The final results were calculated from the fusion model, which can be formulated as:
$$\hat{x}=\mathop{\arg min}_{x}\frac{1}{2}{\|{F_u}x-y\|}_2^2+\frac{\lambda_1}{2}\|\nabla x-\nabla x_{CNN}\|_2^2+\frac{\lambda_2}{2}\|x-x_{CNN}\|_2^2$$
Where x denotes the MRI to be reconstruct, y is the k-space data, and $$$F_u$$$ represents the under-sampled Fourier encoding matrix. The data fidelity term $$$\|F_ux-y\|_2^2$$$ is employed to guarantee the consistence between the Fourier coefficient of the reconstructed image and measured data. R(x) is a sparsifying transform term imposed the $$$l_p$$$ norm (0≤p≤1) and a factor to balance the two terms. $$$x_{CNN}$$$ represents the results reconstructed from MDN, $$$\nabla x$$$ and $$$\nabla x_{CNN}$$$ represent gradient images and results from SRLN respectively. $$$\lambda_1$$$ and $$$\lambda_2$$$ are regularization parameters.
Data acquisition
The MRI dataset consisting of 38 subjects (17 males, and 21 females) were scanned twice on a 1.5 T MRI with an interval of 6-12 months. The T2-weighted images were obtained using a turbo spin echo pulse sequence and the parameters are as follows: TR=4408 ms, TE=100 ms, ES=10.8 ms. The MRA dataset consisting of 15 subjects (8 males, and 7 females) were acquired on a 3.0 T MRI scanner in the use of a gradient recalled echo sequence and the parameters are as follows: TR=23 ms, TE=3.45 ms, FOV=200 mm, NEX=1.00, Thk=0.7 mm, matrix size = 288×286.
Results
The CSMRI reconstruction results shown in Figure 2 demonstrate that the visual quality of the proposed fusion model outperformed other methods (DLMRI2, TV-CSMRI4, LRLs6, U-net5 and MDN6), providing a better preservation for structural details. The deep learning-based methods have some artifacts existing in the background, however, these algorithms have finer image structural information which can be noticed in error residual images. According to Table 1, the fusion model generalizes well for MRI data using three sampling masks with different sampling rates. To demonstrate the capacity of the fusion model, we conducted the simulation experiments of several methods on the MRA dataset. The Maximum Intensity Projection of reconstruction results illustrate that the proposed model obtained better image details during the reconstruction process (Figure 3). Furthermore, we discussed whether the proposed fusion model is beneficial to deep learning-based CS-MRI algorithms. The fusion model based on the compared three CNNs presented a growth trend of reconstruction results using different sampling masks as shown in Figure 4.Conclusion
The proposed fusion model can optimize results (less artifacts and more detailed information) than some optimization-based and deep learning-based methods, using under-sampled MRI and MRA data.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 81971583 and No. 62001120), National Key R&D Program of China (No. 2018YFC1312900), Shanghai Natural Science Foundation (No. 20ZR1406400), Shanghai Municipal Science and Technology Major Project (No.2017SHZDZX01, No.2018SHZDZX01), Shanghai Sailing Program (No. 20YF1402400) and ZJLab.References
- Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6);1182–95.
- Ravishankar S, Bresler Y, MR image reconstruction from highly undersampled k-space data by dictionary learning, IEEE Transactions on Medical Imaging. 2012;30; 1028-1041.
- Ding X, Paisley J, Huang Y, et al. Compressed sensing MRI with Bayesian dictionary learning. ICIP. 2013;2319-2323.
- Haldar J, Hernando D, Liang Z. Compressed-sensing MRI with random encoding. IEEE transactions on Medical Imaging. 2010;30;893-903.
- Lee D, Yoo J, Ye J C. Deep residual learning for compressed sensing MRI. ISBI. 2017;15-18.
- Dai Y, Zhuang P. Compressed sensing MRI via a multi-scale dilated residual convolution network. Magnetic resonance imaging. 2019;63;93-104.
Figures
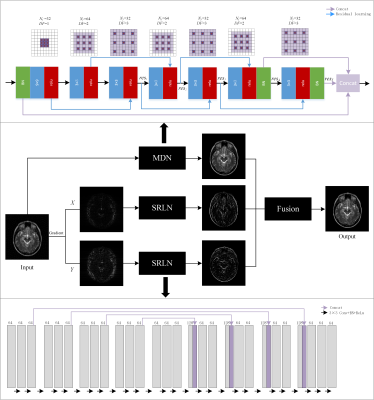
Figure 1 The framework of the
proposed fusion model in which the above network is MDN and the below network is
SRLN. $$$N_f$$$ represents the number
of convolutional kernels, DF represents
the dilated factor of convolutional kernel. $$$c_n$$$ and $$$res_n$$$ represent n-th
convolution layer and residual learning respectively.
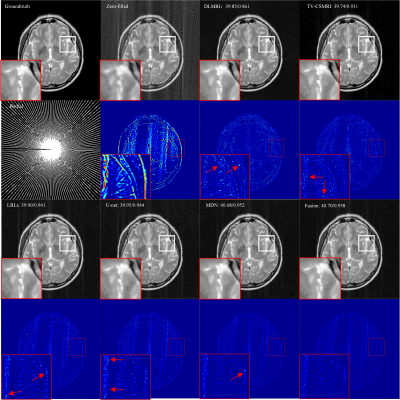
Figure 2 Reconstruction
results for 30% radial sampling. The first and third row include groundtruth
and reconstruction results of CSMRI methods. The second and fourth row include
radial sampling mask and errors. Values of PSNR and SSIM are shown in the upper
left corner.
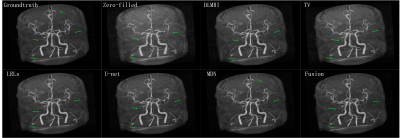
Figure 3 The Maximum
Intensity Projection of the reconstruction results for 40% cartesian sampling
on MRA.
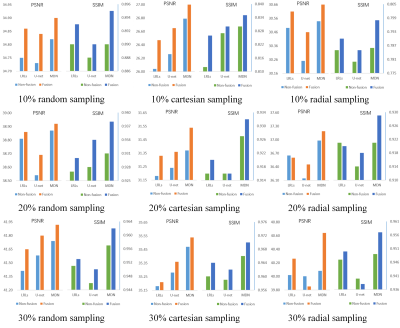
Figure 4 PSNR/SSIM values of
non-fusion and fusion models, which are conducted using three sampling masks
with different sampling rates.
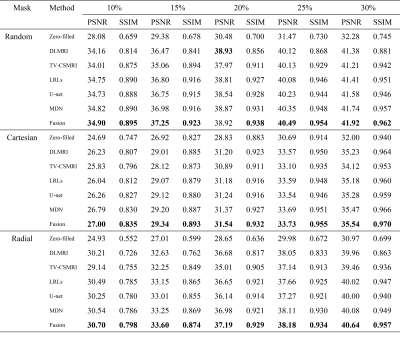
Table 1 Average PSNR/SSIM of
different methods on 50 brain MRI as a function of sampling percentage. The
values in bold font indicate ranking the first place.