1976
Enhanced Multi-Slice Partial Fourier MRI Reconstruction Using Residual Network
Linshan Xie1,2, Yilong Liu1,2, Linfang Xiao1,2, Peibei Cao1,2, Alex T. L. Leong1,2, and Ed X. Wu1,2
1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China
1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China
Synopsis
In this work, we proposed a residual network based reconstruction method for multi-slice partial Fourier acquisition, where adjacent slices are sampled in a complementary way. The anatomical structure and phase similarity of multi-slice MR data can be exploited to provide complementary information from adjacent slices with different sampling patterns. The proposed method enables highly partial Fourier imaging without noise amplification.
Introduction
Partial Fourier (PF) magnetic resonance imaging (MRI) has received abundant attention due to its potential in reducing the echo time or scan time1. Limited symmetrically sampled central k-space region will undermine the phase estimation accuracy, leading to degraded performance of traditional PF reconstruction, such as the projection-onto-convex-sets (POCS) method2. In recent years, multi-slice MR reconstruction has demonstrated its great potential in exploiting the similarities in image contents and coil sensitivity maps in adjacent slices3,4. The image phase across adjacent slices should also be similar due to the slow variation of the main magnetic field and coil sensitivity maps. The multi-slice nature allows adjacent slices with different sampling patterns, providing complementary information across different slices3.In this study, we proposed to jointly use multiple consecutive slices for reconstruction using residual network (ResNet), which can be further enhanced by sampling adjacent slices in a complementary manner. The proposed method can fully exploit structural and phase similarity in adjacent slices to synthesize missing k-space data.
Method
Proposed MethodOur preliminary study explored the feasible of using deep learning for PF reconstruction, which was applied for individual slices, termed as single-slice partial Fourier reconstruction (SS-PF)5. In this study, we propose to jointly use multiple partial-Fourier acquired slices for reconstruction. The proposed multi-slice partial Fourier (MS-PF) reconstruction can be further enhanced by sampling adjacent slices in a complementary manner, termed as EMS-PF. In brief, odd/even slices opposite halves of k-space are sampled for either readout or phase-encoding directions. Figure 1 illustrates the flowchart of the proposed EMS-PF method, where 3 consecutive slices are jointly used for reconstructing the central slice. The input of the network has 6 concatenated channels for the real and imaginary parts of images from 3 consecutive slices. The output has 2 channels for the real and imaginary parts of the estimated residual image for the central slice. After that, the final reconstructed image is obtained by adding the residual image to the image reconstructed from zero-padding k-space.
Model Training and Evaluation
The knee datasets from the Center for Advanced Imaging Innovation and Research (CAI2R)6 were used for training, validating, and testing in the work. The coronal proton density weighted knee data were acquired using 2D fast spin echo (FSE), with TR=2200-3000ms, TE=27-34ms, FOV=160×160mm2, matrix size=320×320, slice thickness/gap=3/0mm. The data were acquired using a 15-channel knee coil, but combined to approximate single-channel acquisition. The datasets contained 942 subjects (each has 16 slices), 70%, 15%, and 15% of which were used for training, validation, and testing, respectively. The raw k-space was cropped to 128×128, retrospectively undersampled along phase-encoding direction at PF fraction of 51%, 55%, and 65%. At PF fraction=51%, with only 4 symmetrically central k-space lines, it would be extremely challenging for conventional POCS reconstruction. Models for reconstructing the odd/even slices were trained separately, as their sampling patterns differed from each other. It took ~3 hours to train each model with 100 epochs. The performance was quantitatively evaluated by the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM).
Although trained with knee data only, the proposed method was also evaluated with human brain datasets acquired on a 3T Philips MRI scanner using a single-channel head coil. T2-weighted images were acquired using 3D FSE with TR/TE=2500/213ms, FOV=240×240×120mm3, matrix size=240×240×120. T1-weighted images were acquired using 3D GRE with TR/TE=19/4ms, flip angle=30°, FOV=240×240×130mm3, matrix size=240×240×130. 1D inverse Fourier transform was applied to the raw k-space, generating 2D k-space for multiple consecutive axial slices with slice thickness/gap=1/0mm. The generated 2D k-space was cropped to 128×128 to fit the trained models, retrospectively undersampled along phase-encoding direction.
Results
Figures 2 and 3 compare the reconstruction results and corresponding error maps for the conventional POCS, and our proposed SS-PF/MS-PF/EMS-PF methods. Note that at PF fraction=51%, the performance of conventional POCS reconstruction degraded dramatically due to insufficient central k-space data for phase estimation. The proposed EMS-PF method showed the best performance on recovering image details without noise amplification among the aforementioned approaches. The MS-PF method and SS-PF method had similar performance, which suggested that without complementary sampling across adjacent slices, jointly using multiple slices for reconstruction cannot fully exploit their structural and phase similarities. Figure 4 illustrates that the EMS-PF method yields slightly higher error as the PF fraction decreased, while the performance of the POCS method experiences a substantial deterioration. This demonstrates the proposed EMS-PF enables highly partial Fourier imaging. Figure 5 presents reconstructed image from T1-weighted/T2-weighted brain images, demonstrating the robustness of the proposed EMS-PF method for MR data of different anatomical regions and/or acquired with different sequences.Discussion and Conclusion
Our proposed method exploits the structural and phase similarity in adjacent slices to synthesize the missing k-space in the slice to be reconstructed, which is superior in preserving the image details without amplifying noise, especially for highly partial Fourier imaging. Note that the slice thickness/gap will affect the performance of the proposed approach as increased slice thickness/gap decreases similarities of adjacent slices, which can be considered by adjusting the number of jointly used slices. Future studies will also adapt the proposed approach for 2D partial Fourier imaging, multi-channel MR acquisition, and/or integrated with parallel imaging.Acknowledgements
This study was supported by Hong Kong Research Grant Council (R7003-19, C7048-16G, HKU17112120, HKU17103819 and HKU17104020), Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001), and Guangdong Key Technologies for Alzheimer’s Disease Diagnosis and Treatment (2018B030336001).References
- Margosian, Paul M., DeMeester, Gordon, and Liu, Haiying. "Partial Fourier Acquisition in MRI." Encyclopedia of Magnetic Resonance. Highland Heights: Picker International, 2007.
- Koopmans, Peter J., and Pfaffenrot, Viktor. "Enhanced POCS reconstruction for partial Fourier imaging in multi-echo and time-series acquisitions." Magnetic Resonance in Medicine 85.1 (2020): 140-151.
- Liu, Yilong, et al. "Calibrationless parallel imaging reconstruction for multislice MR data using low-rank tensor completion." Magnetic Resonance in Medicine 85.2 (2020): 897-911.
- Weizman, Lior, et al. "Exploiting similarity in adjacent slices for compressed sensing MRI." 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE, 2014.
- Cao, Peipei, et al. "Partial Fourier MRI Reconstruction Using Convolutional Neural Networks." Proceedings of International Society of Magnetic Resonance in Medicine. 2020.
- Knoll, Florian, et al. "Welcome to the fastMRI Dataset. " NYU Langone Health. https://fastmri.med.nyu.edu/. Accessed 14 October 2020.
Figures

Figure 1 The flowchart of the
proposed EMS-PF reconstruction method, with adjacent slices having complementary
sampling patterns. Re and Im denote the real and imaginary parts
of the reconstructed slice (Slice 2) and its adjacent slices (Slices 1 and 3); Re2’ and Im2’ denote the real and imaginary parts of the predicted residual
image. The ResNet model has 16 RBs and each of them contains 2 convolutional
layers followed by Rectified Linear Unit (ReLU) activation function. In each
convolutional layer, 64 convolutional kernels of size 3×3 each are included.
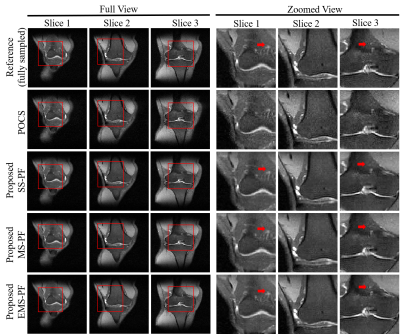
Figure 2
Reconstruction of conventional POCS and proposed SS-PF/MS-PF/EMS-PF for highly
partial Fourier imaging (PF fraction=51%). The corresponding zoomed view is
shown on the right. Images details indicated by the red arrows were best
preserved in the EMS-PF results.
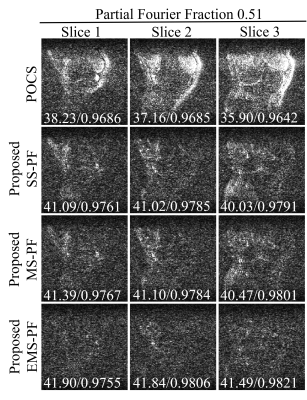
Figure 3 Error maps of the
reconstructed images in Figure 2 with enhanced brightness (×10) and
corresponding peak signal-to-noise ratio (PSNR) / structural
similarity (SSIM) at PF fraction=0.51. It was obvious that the proposed EMS-PF
outperformed the other methods in terms of reduced residual error.
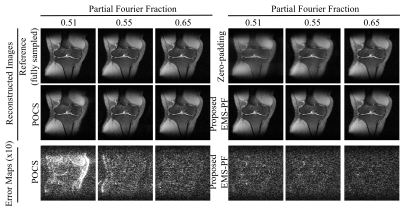
Figure 4
Comparison between the proposed EMS-PF reconstruction and the conventional POCS
method for varying PF factors (0.51, 0.55, and 0.65). With
larger portion of data omitted, the EMS-PF method suffered a slightly higher residual
error, while the performance of the POCS method substantially deteriorated.
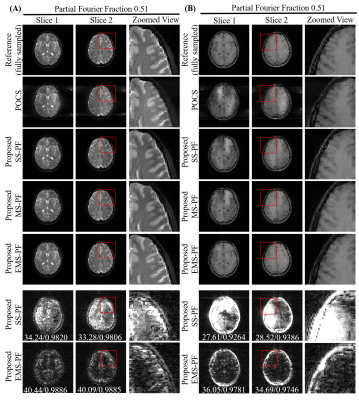
Figure 5 Evaluation with (A) T2-weighted
fast spin echo and (B) T1-weighted gradient echo brain images with highly
partial Fourier imaging (PF fraction=0.51). The proposed EMS-PF method had
substantially reduced residual error compared to the other methods. Error maps (brightness
× 10) and quantitative assessment (PSNR / SSIM) in the last two rows suggested that
our proposed EMS-PF approach outperformed the SS-PF method.