Introduction

In 2D Dynamic Cardiac Cine MR, the data-acquisition process is usually performed during a single breathhold of the patient in order to reduce respiration-related motion artefacts. Undersampling the $$$k$$$-space accelerates this process but leads to an ill-posed reconstruction problem. Thus, regularization methods must be used to properly reconstruct images with diagnostic quality. Dictionary Learning (DL) and Sparse Coding (SC) are well-known and established methods based on local model-assumptions, i.e. patch-wise sparsity. While DL and SC have been successfully applied for MR image reconstruction^1,2 and do not require ground-truth data for training, the SC of the image-estimates during the reconstruction makes the reconstruction inherently slow. Convolutional Neural networks (CNNs), have been recently widely applied for MR image reconstruction as learned regularizers^3,4. They provide a global model with which an image can be processed very quickly. On the other hand, they require ground-truth data for training and can typically be applied only once since they correspond to learned mappings between two fixed manifolds.
Here, we combine DL and SC with CNNs in order to accelerate the data-acquisition process as well as the reconstruction algorithm.

Methods

We formulate the reconstruction problem as a joint optimization problem over the image, an overcomplete dictionary $$$\mathbf{\Psi}$$$ and a set of sparse codes $$$\{\boldsymbol{\gamma}_j \}_j$$$ by further including a penalty term which imposes the solution to be close to a CNN-based image prior which is previously obtained from a pre-trained CNN $$$f_{\Theta}$$$ with trainable parameters $$$\Theta$$$, i.e.
$$ \min_{\mathbf{x},\mathbf{\Psi},\{\boldsymbol{\gamma}_j \}_j} \frac{1}{2}\|\mathbf{A}\mathbf{x} - \mathbf{y} \|_2^2 + \frac{\lambda_{\mathrm{CNN}}}{2}\|\mathbf{x} - \mathbf{x}_{\mathrm{CNN}} \|_2^2+ \frac{\lambda_{\mathrm{DL/SC}}}{2} \sum_j \big(\| \mathbf{R_j} \mathbf{x} -\mathbf{\Psi}\boldsymbol{\gamma}_j \|_2^2 + \|\boldsymbol{\gamma}_j \|_0\big),$$
where $$$\mathbf{A}$$$ denotes a non-uniform FFT (NUFFT) encoding operator, $$$\lambda_{\mathrm{CNN}}, \lambda_{\mathrm{DL/SC}}>0$$$ and $$$\mathbf{x}_{\mathrm{CNN}} := f_{\Theta}( \mathbf{x}_I)$$$ denotes the CNN-output given the initial reconstruction $$$ \mathbf{x}_I:= \mathbf{A}^{\dagger} \mathbf{y}$$$ where $$$\mathbf{A}^{\dagger}:=\mathbf{W}\mathbf{A}^H$$$ with $$$\mathbf{W}$$$ being a diagonal-operator containing the entries of the density-compensation function.

The network $$$f_{\Theta}$$$ is given by a data-consistent CNN, i.e. a CNN-block followed by a subsequent conjugate gradient (CG)-block which can be trained end-to-end. The CNN-block consists of a 2D spatio-temporal U-Net which reduces the undersampling artefacts in spatio-temporal domain by the XT,YT-method⁵. The CNN is used to generate $$$\mathbf{x}_{\mathrm{CNN}}$$$ from $$$\mathbf{x}_I$$$, which serves as a starting point for subsequent iterative reconstruction which alternates between SC, DL and an image-update stage via a CG method. As DL and SC algorithms, we use an adaptive version of the iterative thresholding and K residual means (aITKrM)⁶ and adaptive orthogonal matching pursuit (aOMP)⁷.
We evaluated the proposed reconstruction algorithm on 36 2D cine MR images of 4 patients which were acquired during a single breathhold of approximately 10s (TR/TE=3.0/1.5ms, FA 60$$$^{\circ}$$$) using a bSSFP sequence on a 1.5T MR scanner. The spatial dimensions were $$$N_x \times N_y=320×320$$$ with an in-plane resolution of 2 mm and a slice-thickness of 8 mm. The number of cardiac phases was $$$N_t=30$$$. The images were reconstructed using $$$kt$$$-SENSE⁸ by sampling the $$$k$$$-space data along $$$N_{\theta}=3400$$$ (i.e. $$$R=3$$$) radial spokes. Note that $$$R=3$$$ was needed to perform the scan during a single breathhold of the patients.
From these images, we retrospectively simulated a golden-angle radial data-acquisition⁹ with 12 receiver coils with an undersampling of approximately $$$R=18$$$ (i.e. $$$N_{\theta}=560)$$$ and $$$R=9$$$ (i.e. $$$N_{\theta}=560)$$$.

The CNN was pre-trained on a separate set of 144 2D images using the $$$L_2$$$-error as loss-function. We compared the proposed method to an iterative reconstruction method which uses the CNN-output as image-prior¹⁰ and a method using DL and SC⁷ in terms of peak signal-to-noise ratio (PSNR), normalized root-mean-squared error (NRMSE) and structural similarity index measure (SSIM).

Results

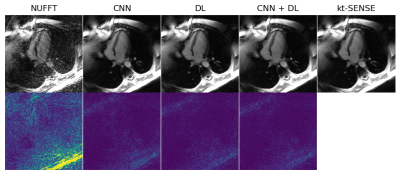
From Figure 1, we see that all three methods succesfully removed the undersampling artefacts from the initially reconstructed image. As can be seen in Table 1, the combination of CNN + DL led to the best results with respect to all measures. The strongest improvements were with respect to PSNR and NRMSE, while for SSIM, the impact was lower.
From Figure 2, we also see that the proposed reconstruction algorithm leads to a faster convergence of the image estimates compared to method only using DL and SC.
Figure 3 shows another example of a dynamic image where we can see the images as well as the point-wise error-images over the whole cardiac cycle.

Discussion & Conclusion

Combining CNNs and DL and SC led to an improvement in image quality compared to using each component separately. Using the CNN-estimate as a starting point for the iteration, faster convergence is achieved compared to DL+SC.Further, although the CNN-output already provides a "good" image estimate, the adaptive DL and SC further refine possibly lost image details as well as further reduce locally present image noise which was not removed by the CNN and thus the combination further improves the reconstruction results compared to the CNN-based approach.

Conclusion

The proposed reconstruction algorithm combines a global and a local model given by a pre-trained CNN and DL and SC, respectively. It yields higher image quality than using either CNNs or DL+SC separately and in addition, highly reduces reconstruction times required by DL+SC due to faster convergence given by the suitable starting point which is obtained with the CNN.

Acknowledgements

No acknowledgement found.