1969
Accelerated Magnetic Resonance Spectroscopy with Model-inspired Deep Learning1Department of Electronic Science, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China, 2School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China, 3Department of Chemistry and Molecular Biology, University of Gothenburg, Gothenburg, Sweden
Synopsis
Multi-dimensional nuclear magnetic resonance (NMR) spectroscopy is an invaluable biophysical tool but often suffers from long measurement. Several methods have been established for spectra reconstruction from undersampled data, two of which are model-based optimization and data-driven deep learning. Combining the main merits of them, we present a model-inspired flexible deep learning framework, for reliable, robust, and ultra-fast spectra reconstruction. Besides, we demonstrate that the model-inspired network needs very few parameters and is not sensitive to training datasets, which greatly reduces the demand for memory footprints and can work effectively in a wide range of scenarios without re-training.
Purpose
NMR spectroscopy serves as an indispensable biophysical tool in modern chemistry and life science. Since the duration of NMR experiments increases rapidly with dimensionality, the non-uniform sampling (NUS) approach1, 2 is commonly used for accelerating the measurement. Over the past two decades, many remarkable methods have been established in the NMR field to reconstruct high-quality spectra from NUS data. Two main strategies of them are model-based optimization1-14 and data-driven deep learning15-19. The former has the explicit structure with insights from NMR spectroscopy but needs lengthy computational time, while the latter greatly reduces the reconstruction time but is trained as a black-box17 and is almost over-parameterized. In this work, we demonstrate the effectiveness of merging optimization and deep learning. The proposed method enables 10 times faster spectra reconstruction than optimization methods, and has 10 times fewer parameters than the existing deep learning method. Besides, it is not sensitive to the training dataset and can work effectively in a wide range of scenarios without re-training.Method
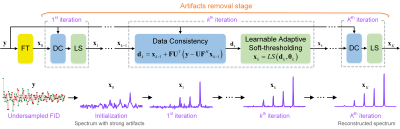
The proposed Model-inspired Deep learning framework, called MoDern, its design of architecture starts from the sparse prior and adopts the main idea from the compressed sensing (CS) algorithm: iterative soft-thresholding (IST)6, 19. Let $$$\bf r$$$ be the complete NMR time-domain signal, and the forward Fourier transform $$$\bf F$$$ converts it into a NMR spectrum $$$\bf x=Fr$$$ . In NMR spectroscopy, the CS model states that the sparsest solution can be always found by the $$$l\scriptsize 1$$$ norm optimization6, 7, 19. This task can be efficiently solved by the IST algorithm, and its $$$k^{th} (k=1,...,K)$$$ iteration process can be written as follows6, 19:$${({\bf Data\ Consistency}):\ {\bf d}_{k}={\bf x}_{k-1}+{\bf FU}^{T}({\bf y}-{\bf UF}^{H}{\bf x}_{k-1}),\ (1a)}$$$${({\bf Soft-thresholding}):\ {\bf x}_{k}=S({\bf d}_{k},\theta),\ (1b)}$$where $$$\bf y$$$ is the FID signal undersampled by operator $$$\bf U$$$, $$${\bf F}^{H}$$$ is the inverse Fourier transform, $$$\bf d$$$ is the spectrum after data consistency, the superscript $$$T$$$ is the transpose operator, $$$\theta$$$ is the threshold, and $$$S(\cdot,\theta)=sgn(\cdot)\times max(0,\mid \cdot\mid-\theta)$$$ is the soft-thresholding operator. Initialized with $$${\bf x}_{0}={\bf FU}^{T}{\bf y}$$$ , CS reconstructs the spectrum by alternating the data consistency and soft-thresholding.Once the overall number of iterations is fixed, the data flow can be viewed as an unfolded deep learning network, as shown in Figure 1. Same to Eq. (1a), the spectrum is forced to maintain the data consistency to the sampled signal. Since the proper choice of thresholds is still of great demand and challenge, thus, instead of Eq. (1b), we use a learnable network $$$LS$$$ which can change thresholds with the characteristics of the input data, for adaptive soft-thresholding. The single network $$$LS$$$ is composed of convolutional layers, fully-connected layers, and a soft-thresholding. The overall number of iterations in our implementation is 10. With the increase of iterations, artifacts are gradually removed, and finally a high-quality reconstructed spectrum can be obtained.
Given a proof-of-concept of training neural networks using solely synthetic data with the exponential functions has been presented in paper15, we also employ this scheme to train our network to learn the best internal parameters and an optimal mapping $$$f$$$ by minimizing the mean square error between outputs of the learnable adaptive soft-thresholding and fully sampled spectra. For a well-trained network, the spectrum can be reconstructed reliably and fastly from an undersampled signal via $$$f$$$ .
Results
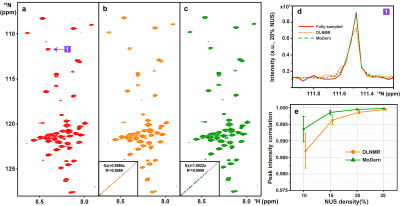
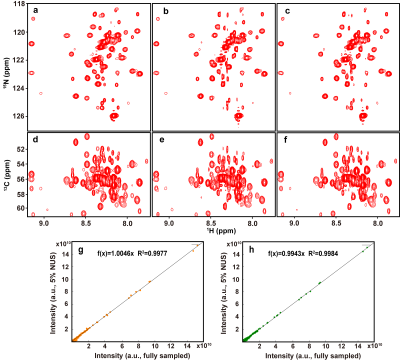
To demonstrate the reliability of the proposed MoDern on experimental data, we reconstruct several spectra under NUS. Herein, we show two of them: 2D HSQC spectrum from cytosolic CD79b and 3D HNCACB of GB1-HttNTQ7 protein. Pearson correlation coefficient R2 is calculated as a measure of the peak intensity correlations between the fully sampled spectra and the reconstructed spectra.The reconstruction of 2D spectra in Figure 2 shows that, (a) MoDern can faithfully reconstruct it using 20% NUS data, and its peak intensity correlation reached 0.9998 with high fidelity of the lineshape reconstruction. (b) MoDern is comparable with, or may even surpass the state-of-the-art reconstruction method DLNMR15 in spectra quality, while being robustness and can maintain excellent performance at low NUS densities. For the reconstruction of 3D spectra in Figure 3 shows that, similar to DLNMR, MoDern also has great potential in fastly high-quality reconstruction, the peak intensity correlation can reach 0.99 even at 20 times acceleration.
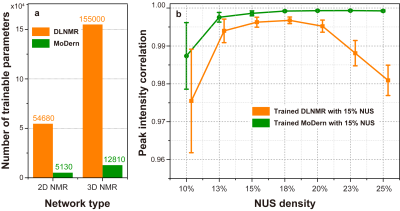
The most important advantage is that, MoDern abandons a large number of redundant convolution layers, which is often used in the data-driven deep learning15, 16, to achieve the dramatic reduction of trainable parameters and computational complexity. Figure 4 shows that, (a) The parameters of MoDern is ca. 9% of that needed for DLNMR, resulting in a significant reduction in network training time and reconstruction time without loss of spectral reconstruction quality. (b) MoDern is very flexible and robust, which means it is not sensitive to spectra sizes, types, and NUS densities. So that, re-training of MoDern is not necessary and it may alleviate the common “mismatch” problem in practice.
Conclusion
In summary, we propose a model-inspired deep learning framework, called MoDern, as a reliable, robust, and ultra-fast technique for obtaining high-quality spectra from NUS data. This work is a powerful demonstration of the effectiveness of merging optimization and deep learning in biological NMR.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (NSFC) under grants 61971361, 61871341, and U1632274, the Joint NSFC-Swedish Foundation for International Cooperation in Research and Higher Education (STINT) under grant 61811530021, the National Key R&D Program of China under grant 2017YFC0108703, the Natural Science Foundation of Fujian Province of China under grant 2018J06018, the Fundamental Research Funds for the Central Universities under grant 20720180056, the Xiamen University Nanqiang Outstanding Talents Program, the Science and Technology Program of Xiamen under grant 3502Z20183053, the Swedish Research Council under grant 2015–04614, and the Swedish Foundation for Strategic Research under grant ITM17-0218.
The correspondence should be sent to Prof. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)
References
[1] V. Jaravine, I. Ibraghimov, and V. Yu Orekhov, "Removal of a time barrier for high-resolution multidimensional NMR spectroscopy," Nature Methods, vol. 3, no. 8, pp. 605-607, 2006.
[2] M. Mobli and J. C. Hoch, "Nonuniform sampling and non-Fourier signal processing methods in multidimensional NMR," Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 83, pp. 21-41, 2014.
[3] J. Ying, F. Delaglio, D. A. Torchia, and A. Bax, "Sparse multidimensional iterative lineshape-enhanced (SMILE) reconstruction of both non-uniformly sampled and conventional NMR data," Journal of Biomolecular NMR, vol. 68, no. 2, pp. 101-118, 2017.
[4] X. Qu, X. Cao, D. Guo, and Z. Chen, "Compressed sensing for sparse magnetic resonance spectroscopy," in International Society for Magnetic Resonance in Medicine 19th Scientific Meeting, 2010, p.3371.
[5] X. Qu, D. Guo, X. Cao, S. Cai, and Z. Chen, "Reconstruction of self-sparse 2D NMR spectra from undersampled data in indirect dimension," Sensors, vol. 11, no. 9, pp. 8888-8909, 2011.
[6] K. Kazimierczuk and V. Y. Orekhov, "Accelerated NMR spectroscopy by using compressed sensing," Angewandte Chemie International Edition, vol. 50, no. 24, pp. 5556-5559, 2011.
[7] D. J. Holland, M. J. Bostock, L. F. Gladden, and D. Nietlispach, "Fast multidimensional NMR spectroscopy using compressed sensing," Angewandte Chemie International Edition, vol. 50, no. 29, pp. 6548-6551, 2011.
[8] Y. Shrot and L. Frydman, "Compressed sensing and the reconstruction of ultrafast 2D NMR data: Principles and biomolecular applications," Journal of Magnetic Resonance, vol. 209, no. 2, pp. 352-358, 2011.
[9] X. Qu, M. Mayzel, J.-F. Cai, Z. Chen, and V. Orekhov, "Accelerated NMR Spectroscopy with Low-Rank Reconstruction," Angewandte Chemie International Edition, vol. 54, no. 3, pp. 852-854, 2015.
[10] J. Ying, J.-F. Cai, D. Guo, G. Tang, Z. Chen, and X. Qu, "Vandermonde factorization of Hankel matrix for complex exponential signal recovery—Application in fast NMR spectroscopy," IEEE Transactions on Signal Processing, vol. 66, no. 21, pp. 5520-5533, 2018.
[11] H. Lu, X. Zhang, T. Qiu, J. Yang, J. Ying, D. Guo, Z. Chen, and X. Qu, "Low rank enhanced matrix recovery of hybrid time and frequency data in fast magnetic resonance spectroscopy," IEEE Transactions on Biomedical Engineering, vol. 65, no. 4, pp. 809-820, 2018.
[12] D. Guo, H. Lu, and X. Qu, "A fast low rank Hankel matrix factorization reconstruction method for non-uniformly Sampled magnetic resonance spectroscopy," IEEE Access, vol. 5, pp. 16033-16039, 2017.
[13] J. Ying, H. Lu, Q. Wei, J. -F. Cai, D. Guo, J. Wu, Z. Chen, and X. Qu, "Hankel matrix nuclear norm regularized tensor completion for N-dimensional exponential signals," IEEE Transactions on Signal Processing, vol. 65, no. 14, pp. 3702-3717, 2017.
[14] T. Qiu, Z. Wang, H. Liu, D. Guo, and X. Qu, "Review and prospect: NMR spectroscopy denoising and reconstruction with low-rank Hankel matrices and tensors," Magentic Resonance in Chemistry, 2020, DOI: 10.1002/mrc.5082.
[15] X. Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, T. Agback, V. Orekhov, and Z. Chen, "Accelerated nuclear magnetic resonance spectroscopy with deep learning," Angewandte Chemie International Edition, vol. 59, no. 26, pp. 10297-10300, 2020.
[16] Y. Huang, J. Zhao, Z. Wang, D. Guo, and X. Qu, "Exponential signal reconstruction with deep Hankel matrix factorization," arXiv preprint arXiv:2007.06246, 2020.
[17] D. Chen, Z. Wang, D. Guo, V. Orekhov, and X. Qu, "Review and prospect: Deep Learning in nuclear magnetic resonance spectroscopy," Chemistry –A European Journal, vol. 26, no. 46, pp. 10391-10401, 2020.
[18] S. G. Hyberts, A. G. Milbradt, A. B. Wagner, H. Arthanari, and G. Wagner, "Application of iterative soft thresholding for fast reconstruction of NMR data non-uniformly sampled with multidimensional Poisson Gap scheduling," Journal of Biomolecular NMR, vol. 52, no. 4, pp. 315-327, 2012.
[19] A. Shchukina, P. Kasprzak, R. Dass, M. Nowakowski, and K. Kazimierczuk, "Pitfalls in compressed sensing reconstruction and how to avoid them," Journal of Biomolecular NMR, vol. 68, no. 2, pp. 79-98, 2017.
Figures