1966

Multi-Mask Self-Supervised Deep Learning for Highly Accelerated Physics-Guided MRI Reconstruction

Burhaneddin Yaman^1,2, Seyed Amir Hossein Hosseini^1,2, Steen Moeller², Jutta Ellermann², Kâmil Uğurbil², and Mehmet Akçakaya^1,2
¹University of Minnesota, Minneapolis, MN, United States, ²Center for Magnetic Resonance Research, Minneapolis, MN, United States

Synopsis

Self-supervised physics-guided deep learning (PG-DL) approaches enable training neural networks without fully-sampled data. These methods split the available k-space measurements into two sets. One is used in the data consistency units of the unrolled network, while the other is used to define the loss. Although self-supervised learning performs well at moderately high acceleration rates, scarcity of acquired data at high acceleration rates degrades the reconstruction performance. In this work, we propose a multi-mask self-supervised learning approach, which retrospectively splits acquired measurement into multiple 2-tuples of disjoint sets. Proposed multi-mask self-supervised learning method outperforms its single-mask counterpart at high acceleration rates.

INTRODUCTION

Physics-guided deep learning (PG-DL) approaches which unrolls an iterative optimization problem containing regularizer and data consistency (DC) units for fixed number of iterations has gained interest due to their improved reconstruction quality and robustness^1-8. While PG-DL approaches are typically trained in a supervised manner, this hinders their application to a number of scans where fully-sampled acquisitions are challenging⁹. A recently proposed self-supervised PG-DL method (SSDU)^9,10 enables training neural networks without fully-sampled data by retrospectively splitting available k-space measurements into two sets. One of these is used in the DC units of the unrolled network, while the other is used to define loss. However, scarcity of acquired data at very high acceleration rates degrades the performance SSDU PG-DL approach.

In this work, we propose a multi-mask SSDU PG-DL approach for highly accelerated MRI reconstruction. We apply the proposed multi-mask SSDU PG-DL on 3D knee and brain MRI datasets, showing its utility and improvement compared to single-mask SSDU PG-DL at high acceleration rates.

THEORY

Regularized least squares problem for MRI reconstruction is given as$$\arg\min_{\bf x}\|\mathbf{y}_{\Omega}-\mathbf{E}_{\Omega}\mathbf{x}\|^2_2+\cal{R}(\mathbf{x}),(1)$$where x is the image of interest, $$$\mathbf{y}_{\Omega}$$$ is the acquired measurements with sub-sampling pattern $$$\Omega$$$, $$$\mathbf{E}_{\Omega}$$$ is the multi-coil encoding operator. The first term in Eq.1 enforces DC and $$$\cal{R}(.)$$$ is a regularizer. Eq.1 can be solved in an iterative manner by using variable splitting with quadratic penalty approach as¹¹$$\mathbf{z}^{(i)}=\arg\min_{\bf z}\mu\lVert\mathbf{x}^{(i-1)}-\mathbf{z}\rVert_{2}^2+\cal{R}(\mathbf{z}),(2)$$$$\mathbf{x}^{(i)}=\arg\min_{\bf x}\|\mathbf{y}_{\Omega}-\mathbf{E}_{\Omega}\mathbf{x}\|^2_2+\mu\lVert\mathbf{x}-\mathbf{z}^{(i)}\rVert_{2}^2,(3)$$where $$$\mathbf{z}^{(i)}$$$ is an intermediate variable, $$$\mathbf{x}^{(i)}$$$ is the output at iteration i and $$$\mu$$$ is the quadratic penalty parameter. In PG-DL, the iterative algorithm in Eq.2 and 3 is unrolled for a fixed number of iterations. In the presence of fully-sampled data, supervised PG-DL approaches perform end-to-end training by minimizing⁹$$\min_{\bf\theta}\frac1N\sum_{i=1}^{N}\mathcal{L}({\bf y}_{\textrm{ref}}^i,\:{\bf E}_{full}^if({\bf y}_{\Omega}^i,{\bf E}_{\Omega}^i;{\bf\theta})),(4)$$
where N is number of datasets in the database, $$${\bf y}_{\textrm{ref}}^i$$$ is the fully-sampled k-space of the i^th subject in the database, $$$f({\bf y}_{\Omega}^i,{\bf E}_{\Omega}^i;{\bf\theta})$$$ denotes network output with parameters θ, $$${\bf E}_{full}^i$$$ is the fully-sampled encoding operator that transform network output to k-space, and $$$\mathcal{L}(\cdot,\cdot)$$$ is training loss.

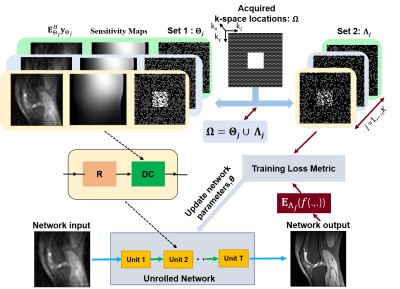
In the absence of fully-sampled data, SSDU PG-DL enables training by splitting acquired data locations $$$\Omega$$$ into two disjoint sets, $$$\Theta$$$ and $$$\Lambda$$$ as $$$\Omega=\Theta\cup\Lambda$$$, where $$$\Theta$$$ and $$$\Lambda$$$ denotes the k-space locations used in DC units and loss function, respectively. SSDU PG-DL training is performed by minimizing⁹$$\min_{\bf\theta}\frac1N\sum_{i=1}^{N}\mathcal{L}\Big({\bf y}_{\Lambda}^i,\:{\bf E}_{\Lambda}^i\big(f({\bf y}_{\Theta}^i,{\bf E}_{\Theta}^i;{\bf\theta})\big)\Big).(5)$$Note that the loss is performed on only locations indicated by $$$\Lambda$$$, which are not seen by the unrolled network itself.

In the proposed multi-mask SSDU PG-DL (Fig. 1), acquired k-space location $$$\Omega$$$ is retrospectively split into multiple 2-tuple of disjoint sets $$$\Theta_j$$$ and $$$\Lambda_j$$$ based on a uniformly random distribution. For each partition, we set $$$\Omega=\Theta_j\cup\Lambda_j$$$ where $$$\Lambda_j=\Omega/\Theta_j$$$ for j=1,…,K. Hence, objective function to minimize for proposed multi-mask SSDU PG-DL approach is as follows$$\min_{\bf\theta}\frac{1}{N\cdot K}\sum_{i=1}^{N}\sum_{j=1}^{K}\mathcal{L}\Big({\bf y}_{\Lambda_j}^i,\:{\bf E}_{\Lambda_j}^i\big(f({\bf y}_{\Theta_j}^i,{\bf E}_{\Theta_j}^i;{\bf\theta})\big)\Big).(6)$$

METHODS

Fully-sampled 3D knee datasets (matrix-size=320×320×256, 8-coils) were obtained from mri-data.org¹². Additionally, 3D MPRAGE brain MRI (matrix-size=320×320×224, ACS lines=40, 32-coils,prospective acceleration(R)=2) was acquired at 3T with IRB approval and written informed consent⁹.

2D slices were processed after taking inverse Fourier transform along the read-out direction for the both 3D k-space datasets. Knee and brain datasets were further retrospectively subsampled to R=8 by keeping 24×24 and 32×32 ACS regions in the k_y-k_z plane using a sheared uniform undersampling pattern, respectively. Training was performed on 300 slices from 10 subjects for both knee and brain datasets. Testing was performed on 8 and 9 new subjects for knee and brain MRI, respectively.

For both knee and brain MRI, networks were trained using Adam optimizer with a learning rate 5×10^-4 by minimizing a mixed normalized $$$\ell_1-\ell_2$$$ loss function over 100 epochs⁹. For all PG-DL approaches, ResNet⁹ and conjugate-gradient² was employed at regularizer and DC units, respectively. Further comparisons were made with CG-SENSE. Experimental results were quantitatively evaluated using SSIM and NMSE.

RESULTS

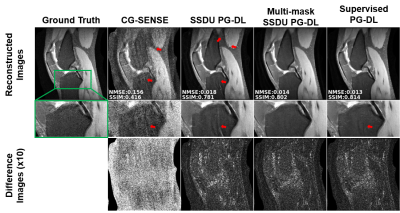
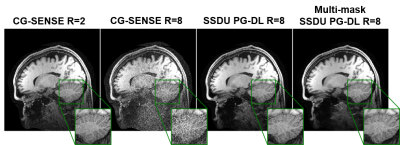
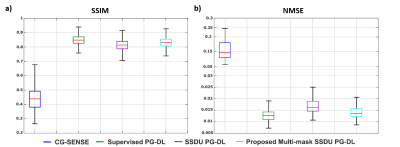
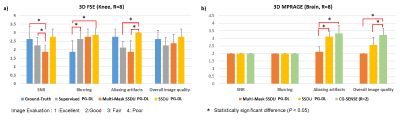
Fig. 2 shows reconstruction results for knee MRI. CG-SENSE suffers from significant residual artifacts. Proposed multi-mask SSDU PG-DL outperforms SSDU PG-DL, while also showing a better performance compared to supervised PG-DL in terms of reducing residual artifacts. Fig. 3 displays reconstruction results from brain MRI for SSDU PG-DL, multi-mask SSDU PG-DL at R=8 as well as CG-SENSE at R=2 and 8. SSDU at R=8 show similar reconstruction quality with CG-SENSE at R=2, while CG-SENSE at R=8 suffers from major noise amplifications. Proposed multi-mask SSDU at R=8 improves upon SSDU at R=8 by suppressing noise level further. Supervised PG-DL is not available in this setting due to lack of fully-sampled data. Fig. 4 depicts average quantitative metrics from knee MRI. Fig. 5 summarizes average reader scores for knee and brain MRI.

DISCUSSION

In this study, we proposed a multi-mask SSDU PG-DL training method for MRI reconstruction without using fully-sampled data by retrospectively splitting available measurements into multiple 2-tuples of disjoint sets. Results on knee and brain MRI at high acceleration rates showed that multi-mask SSDU improves upon SSDU. Interestingly, while supervised PG-DL achieved higher quantitative metrics and was ranked higher for overall image quality, multi-mask SSDU showed better performance in terms of removing residual artifacts in the reader study.

CONCLUSIONS

Our proposed multi-mask SSDU PG-DL approach efficiently reuses available measurement and improves upon SSDU PG-DL training without fully-sampled data.

Acknowledgements

Grant support: NIH P30NS076408, NIH 1S10OD017974-01,NIH R01HL153146, NIH P41EB027061, NIH U01EB025144; NSF CAREER CCF-1651825

References

1. Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med 2018;79(6):3055-3071.

2. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging 2019;38(2):394-405.

3. Hosseini SAH, Yaman B, Moeller S, Hong M, Akcakaya M. Dense Recurrent Neural Networks for Inverse Problems: History-Cognizant Unrolling of Optimization Algorithms. IEEE Journal of Selected Topics in Signal Processing 2020;14(6):1280-1291.

4. Liang D, Cheng J, Ke Z, Ying L. Deep Magnetic Resonance Image Reconstruction: Inverse Problems Meet Neural Networks. IEEE Signal Processing Magazine; 2020. p 141-151.

5. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2018;37(2):491-503. 6. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2019;38(1):280-290.

7. Tamir JI, Yu SX, Lustig M. Unsupervised Deep Basis Pursuit: Learning inverse problems without ground-truth data. Advances in Neural Information Processing Systems Workshops; 2019.

8. Kellman M, Zhang K, Tamir J, Bostan E, Lustig M, Waller L. Memory-efficient Learning for Large-scale Computational Imaging. arXiv:2003.05551; 2020.

9. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Uğurbil K, Akçakaya M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn Reson Med 2020;84(6):3172-3191.

10. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Ugurbil K, Akcakaya M. Self-Supervised Physics-Based Deep Learning MRI Reconstruction Without Fully-Sampled Data. IEEE 17th International Symposium on Biomedical Imaging (ISBI); 2020. p 921-925.

11. Fessler JA. Optimization Methods for Magnetic Resonance Image Reconstruction: Key Models and Optimization Algorithms. IEEE Signal Process Mag 2020;37(1):33-40.

12. Ong F, Amin S, Vasanawala S, Lustig M. Mridata. org: An open archive for sharing MRI raw data. Proceedings of the 26th Annual Meeting of ISMRM.

Figures

Figure 1. Proposed multi-mask SSDU PG-DL scheme. Acquired sub-sampled k-space locations for each scan Ω, are split into multiple disjoint sets, Θ_j and Λ_j in which Λ_j= Ω / Θ_j, for j ∈ 1, …, K. For each partitioning, Θ_j is used in data consistency unit of the unrolled network and Λ_j is used to define the loss function for training. During training available subset of measurements at Λ_j, are compared with the corresponding reconstructed k-space values obtained by transforming network output to k-space at Λ_j locations. Subsequently, the network parameters are updated based on the training loss.

Figure 2. a) Reconstruction results on a representative test slice at R = 8 using CG-SENSE, supervised PG-DL, SSDU PG-DL and proposed multi-mask SSDU PG-DL. CG-SENSE suffers from major noise amplification and artifacts. SSDU PG-DL also shows residual artifacts (red arrows) at this high acceleration rate. Proposed multi-mask SSDU PG-DL further suppresses these artifacts and achieve artifact-free reconstruction, removing artifacts that are still visible in supervised PG-DL.

Figure 3. A representative test brain MRI slice showing reconstruction results using CG-SENSE, SSDU PG-DL and proposed multi-mask SSDU PG-DL at R=8, as well as CG-SENSE at acquisition acceleration R=2. CG-SENSE suffers from major noise amplification at R=8, whereas SSDU PG-DL at R=8 achieves similar reconstruction quality to CG-SENSE at R=2. The proposed multi-mask SSDU PG-DL further improves the reconstruction quality compared to SSDU PG-DL.

Figure 4. Box plots shows interquartile range (25th-75th percentile) of the a) SSIM and b) NMSE values on test dataset. All PG-DL approaches outperform CG-SENSE in terms of both SSIM and NMSE. Proposed multi-mask SSDU PG-DL outperforms SSDU PG-DL, while closely matching supervised PG-DL in terms of both SSIM and NMSE.

Figure 5. Average reader scores for overall image quality on a 4-point scale (1: excellent, 2: good, 3: fair, 4: poor). For knee MRI, proposed multi-mask SSDU PG-DL received better scores than SSDU PG-DL and similar scores with supervised PG-DL for all evaluation criteria. In brain MRI, all methods were in good agreement in terms of SNR and blurring, while for aliasing artifacts and overall image quality, CG-SENSE at R=2, which is the clinical baseline, received the worst scores, and the proposed multi-mask SSDU PG-DL at R=8 was rated highest.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1966