1962
Non-uniform Fast Fourier Transform via Deep Learning1Center for Biomedical Imaging Research, Medical School, Tsinghua University, Beijing, China, 2MR Research China, GE Healthcare, Beijing, China, 3King’s College London, London, United Kingdom
Synopsis
In this study, a deep learning-based MR reconstruction framework called DLNUFFT (Deep Learning-based Non-Uniform Fast Fourier Transform) was proposed, which can restore the under-sampled non-uniform k-space to fully sampled Cartesian k-space without NUFFT gridding. Novel network blocks with fully learnable parameters were built to replace the hand-crafted convolution kernel and the density compensation in NUFFT. Simulations and in-vivo results showed DLNUFFT can achieve higher performance than conventional NUFFT, compressed sensing and state-of-the-art deep learning methods in terms of PSNR and SSIM.
Synopsis
In this study, a deep learning-based MR reconstruction framework called DLNUFFT (Deep Learning-based Non-Uniform Fast Fourier Transform) was proposed, which can restore the under-sampled non-uniform k-space to fully sampled Cartesian k-space without NUFFT gridding. Novel network layers with fully learnable parameters were constructed to replace the hand-crafted convolution kernel and the density compensation in conventional NUFFT. Simulations and in-vivo results showed DLNUFFT can achieve higher performance than conventional NUFFT, compressed sensing and state-of-the-art deep learning methods in terms of PSNR and SSIM.Introduction
Non-Cartesian trajectories such as radial, propeller and spiral are gaining more research interests because of their insensitivity to motion and higher sampling efficiency [1]. However, reconstruction of non-Cartesian acquisition usually requires non-uniform fast Fourier Transform (NUFFT) which has limitations of long computation time and hand-crafted kernel functions and proper density compensation factors. Moreover, direct NUFFT may produce severe artefacts for undersampled data [2]. Compressed sensing (CS) and deep learning reconstruction methods have been proposed to improve the image quality of undersampled non-Cartesian data. However, CS method typically requires iterative optimization and thus long reconstruction time. Image-domain (learning in image domain) and hybrid-domain (learning alternatively in k-space and image domain) deep learning methods may face the generalization issue when the trained network in one anatomy transfers to other anatomies. Meanwhile, images from NUFFT are often used as the initial guesses, where the gridding errors caused by NUFFT are inevitable [4]. Manifold –learning such as AUTOMAP [5], however, requires large GPU memory and still needs an image-based network to refine the reconstruction results, which suffers from the similar problem in image-domain learning. Current k-space domain leaning methods only utilize the local correlation of k-space because of the nature of the convolutional network used, whereas k-space data are globally correlated.Methods
Network StructureTo address these issues, DLNUFFT was proposed and it was constructed with novel layers including Block Layer (BL), ReBlock Layer (RBL), Density Compensation and Reordering Layer (DCRL) and Adaptive Interpolation Layer (AIL) (Figure 1a).
BL and RBL can divide the k-space data into patches and integrate the patches to their original sizes, respectively. Patches were stacked as different channels. Since different channels contains k-space data from different k-space locations, the global spatial information was encoded in channel dimension.
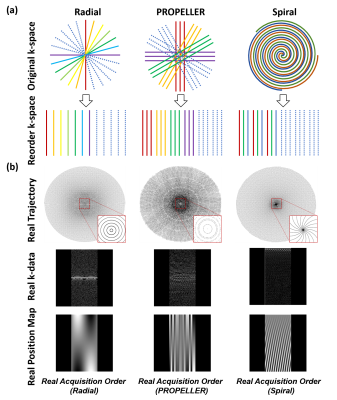
In DCRL, a 1x1 convolution layer with leaky ReLU [6] was used. It can shuffle the channels of the tensor, which was equivalent to the spatial position transformation operation, so the patch can be rearranged from Real Acquisition Order to Cartesian Order (Figure 1b); Additionally, weights in the 1×1 convolution represented the correlation between input channel and output channel, so these weights can be regarded as density compensation factors in NUFFT, which balanced the density of the sampled points.
AIL performed the adaptive k-space interpolation. It was composed of two group convolution layers which learned both the regional and global correlation of k-space data. Specifically, the convolution operation in the single channel can capture local information while the summarization among the channels can capture global information since different channels represented different locations of the image.
Dataset and Training
Input of DLNUFFT was the multi-coil k-space data without NUFFT gridding and was reshaped to the Real Acquisition Order using the position map as the guidance (Figure 2). The position map recorded the k-space position of each acquired data point and different position maps denoted the different sampling trajectories. The output of the network should be the fully sampled Cartesian k-space data and the mean absolute error between the network output and the ground truth was calculated as training loss.
A two-step training strategy was adopted.
1) DLNUFFT was firstly pre-trained on natural images (20000 images) from ImageNet with random sampling trajectories, i.e. random position maps generated from Perlin noise [7], and random phase maps using the method in [8] (Figure 3).
2) Fine-tuned on five MR datasets (T1w, T2w brain, CINE, mDIXON and DCE liver) with commonly used trajectories (radial, spiral and PROPELLER) at different undersampling factors (R = 2, 4, 6). Each dataset contained 3000 images which were divided into training (2000), validation (500) and testing (500) parts.
After training, it took about 23 ms to reconstruct one multi-coil 2D image.
Experiment
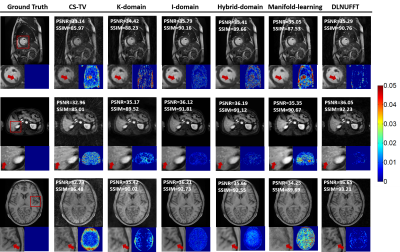
DLNUFFT was compared with CS-TV [9], I-domain [10], K-domain [11], Hybrid-domain [4] and Manifold learning [12] methods. It was first tested in fine-tuned datasets and then performed in in-vivo brain and liver datasets with prospective reconstruction to further validate DLNUFFT. Quantitative analysis was performed in fine-tuning experiments using PSNR and SSIM as evaluation metrics.
Results
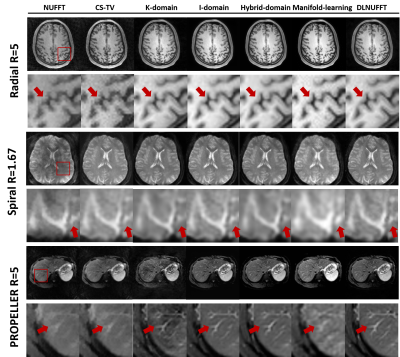
Figure 4 shows reconstruction results of three datasets with radial trajectory (R=4). Images from DLNUFFT had less noise and streaking artifacts. Meanwhile, DLNUFFT achieved relatively high PSNR (36.65dB) and the highest SSIM (93.21%).Figure 5 shows the prospective reconstruction results. DLNUFFT can restore more details of the sulcus and gyrus in brain and small vessels in liver than other methods, showing higher performance as well as good generalization ability.
Discussion and Conclusion
DLNUFFT achieved better reconstruction performance than CS in terms of PSNR and SSIM and outperformed other learning-based methods regarding better generalization ability.Acknowledgements
NoneReferences
1. Chan, R.W., Ramsay, E.A., Cheung, E.Y., Plewes, D.B., 2012. The influence of radial undersampling schemes on compressed sensing reconstruction in breast MRI. Magnet Reson Med 67, 363-377.
2. Desplanques, B., Cornelis, J., Achten, E., van de Walle, R., Lemahieu, I., 2002. Iterative reconstruction of magnetic resonance images from arbitrary samples in k-space. IEEE T Nucl Sci 49, 2268-2273.
3. Feng, L., Grimm, R., Block, K.T., Chandarana, H., Kim, S., Xu, J., Axel, L., Sodickson, D.K., Otazo, R., 2014. Golden-Angle Radial Sparse Parallel MRI: Combination of Compressed Sensing, Parallel Imaging, and Golden-Angle Radial Sampling for Fast and Flexible Dynamic Volumetric MRI. Magnet Reson Med 72, 707-717.
4. Eo, T., Jun, Y., Kim, T., Jang, J., Lee, H.J., Hwang, D., 2018. KIKI-net: cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magnet Reson Med 80, 2188-2201.
5. Zhu, B., Liu, J.Z., Cauley, S.F., Rosen, B.R., Rosen, M.S., 2018. Image reconstruction by domain-transform manifold learning. Nature 555, 487
6. Y, M.A.L.H.A.Y.N.A., 2013. Rectifier Nonlinearities Improve Neural Network Acoustic Models ICML Workshop on Deep Learning for Audio, Speech and Language Processing.
7. Perlin, K., 2002. Improving noise, Proceedings of the 29th annual conference on Computer graphics and interactive techniques. Association for Computing Machinery, San Antonio, Texas, pp. 681–682.
8. Muckley, M.J., Ades-Aron, B., Papaioannou, A., Lemberskiy, G., Solomon, E., Lui, Y.W., Sodickson, D.K., Fieremans, E., Novikov, D.S., Knoll, F., 2020. Training a neural network for Gibbs and noise removal in diffusion MRI. Magnet Reson Med.
9. Rudin, L.I., Osher, S., Fatemi, E., 1992. Nonlinear Total Variation Based Noise Removal Algorithms. Physica D 60, 259-268.
10. Wang, S., Su, Z., Ying, L., Peng, X., Zhu, S., Liang, F., Feng, D., Liang, D., 2016. Accelerating magnetic resonance imaging via deep learning, 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), pp. 514-517.
11. Han, Y., Sunwoo, L., Ye, J.C., 2020. k-Space Deep Learning for Accelerated MRI. Ieee T Med Imaging 39, 377-386.
12. Rueckert, J.S.I.O.J.C.J.D.A.P.K.J.A.S.J.V.H.D., 2019. dAUTOMAP: decomposing AUTOMAP to achieve scalability and enhance performance, ISMRM, Montreal, Canada.
Figures