Introduction

Deep learning (DL) reconstruction algorithms are emerging as powerful alternatives for compressed sensing methods used for accelerated imaging. DL methods rely on convolutional neural networks to learn the inverse of the acquition scheme, which offers significantly improved image quality and super-fast inference.

A challenge with DL algorithms is the potential mismatch between the forward model used during training and the acquisition scheme during inference. While model-based deep learning algorithms (e.g. [1]) that use the forward model can offer good reconstruction performance for small deviations in the acquisition scheme, even they will result in artifacts when the acquisition scheme is significantly different. Several schemes that adapt the model to the measured k-space data using a mean-square loss were introduced to minimize model misfit [5,6]. However, these methods do not account for noise in the measured k-space data. The main focus of this work is to introduce an adaptive training strategy using generalized Stein's unbiased risk estimate (GSURE). GSURE provides an estimate for the loss in the presence of noise, thus minimizing overfitting on the network to the noise.

Proposed Method

The image acquisition model to acquire the noisy and undersampled measurements $$$y$$$ of an image $$$x$$$ using the forward operator $$$\mathcal A$$$ can be represented as $$$y=\mathcal Ax+n$$$. Where $$$n$$$ is the small amount of Gaussian noise that may be present in the measurements. Let $$$\hat{x}$$$ be the reconstructed image using the network $$$f_\Phi$$$ parameterized by network weights $$$\Phi$$$ such that $$$\hat{x}=f_\Phi(y)$$$.
During testing, we can adapt the trained model to a different $$$\mathcal A$$$ operator by performing fine-tuning using mean-square-error (MSE) between the measured and reconstructed k-space as follows:

$$\text{MSE loss in k-space} = \| y-A\hat{x}\|_2^2 \quad ----------------(1) $$
However, this approach may overfit the noisy samples and thus requires manually stopping. We propose to use generalized Stein's unbiased risk estimate (G-SURE) [1] loss function, which explicitly accounts for measurement noise.

$$\text{G-SURE loss} = \underbrace{\| \mathbf P (\hat{x} - u) \|_2^2}_{\text{data-term}} + \underbrace{\mathbb E \left [ \nabla f_\Phi (u) \right ]}_{\text{divergence}} ---------------(2) $$
Here $$$\mathbf P$$$ is a projection operator to the range space of $$$\mathcal A^H$$$, $$$u=\left(\mathcal A^H\mathcal A\right)^{\dagger}\mathcal A^H y$$$ is the SENSE reconstruction. We evaluate the network divergence using the Monte-Carlo method [2]. The detailed derivation of the G-SURE-based loss function for MR image reconstruction can be found in [3]. By reducing overfitting, this approach offers improved reconstruction quality and eliminates the need or manual stopping.

Experiments and Results

We consider a parallel MRI brain data obtained using a 3-D T2 CUBE sequence with Cartesian readouts using a 12-channel head coil at the University of Iowa on a 3T GE MR750w scanner. The matrix dimensions were 256x256x208 with a 1 mm isotropic resolution. Fully sampled multi-channel brain images of nine volunteers were collected, out of which data from five subjects were used for training. The data from two subjects were used for testing and the remaining two for validation.

We utilized a model-based deep learning architecture MoDL [4] in the experiments with three unrolling steps. The network weights were shared over iterations. All experiments used a standard 18-layer ResNet architecture within each unrolling step with 3x3 filters and 64 feature maps at each layer. The real and imaginary components of complex data were used as channels in all the experiments. All the experiments are performed in simulation settings at 6-fold acceleration with a noise standard deviation of 0.02.

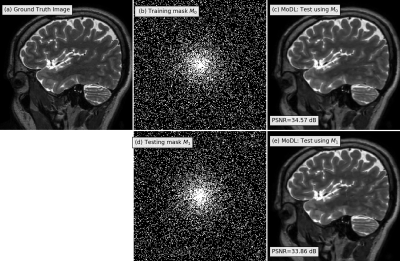
In the first experiment, we trained the MoDL with a variable density mask $$$M_0$$$ as shown in Fig 1(b). When this mask is used for image recovery, MODL offered good recovery (c). When another variable density mask $$$M_1$$$ in (d) is used, the performance only degraded slightly, indicating the robustness of model-based algorithms to slight misfit.

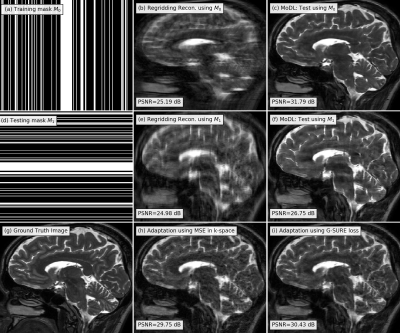
In the second experiment, we consider a more drastic deviation. When a Cartesian mask $$$M_1$$$ in (Fig. 2(d)) that differed significantly from $$$M_0$$$ in (a) was used, the MoDL reconstruction PSNR decayed to 26.75 dB, resulting from image artifacts. The fine-tuning of the network with MSE loss in Eq. 1 and G-SURE loss in Eq. 2 is shown in (h) and (i), respectively. The model adaptation with MSE and G-SURE loss leads to a PSNR of 29.75 dB and 30.43 dB respectively, with GSURE reconstruction exhibiting fewer artifacts.

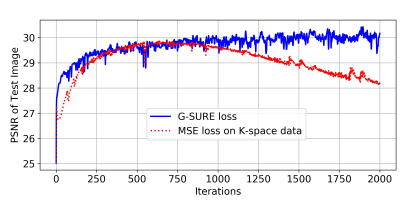
In the third experiment, Fig. 3 shows the comparison of MSE loss and G-SURE loss for model adaptation. We observe that G-SURE loss is more stable due to the utilization of a network divergence term. Thus, the purposed G-SURE-based model adaptation does not require manual stopping to avoid overfitting. In addition, G-SURE loss results in a higher PSNR value as compare to MSE loss.

Acknowledgements

This work is supported by 1R01EB019961-01A1. This work was conducted on an MRI instrument funded by 1S10OD025025-01.