1958
Alignment & joint recovery of multi-slice cine MRI data using deep generative manifold model
Qing Zou1, Abdul Haseeb Ahmed1, Prashant Nagpal1, Rolf Schulte2, and Mathews Jacob1
1University of Iowa, Iowa City, IA, United States, 2GE Global Research, Munich, Germany
1University of Iowa, Iowa City, IA, United States, 2GE Global Research, Munich, Germany
Synopsis
The main focus of this work is to introduce an unsupervised deep generative manifold model for the alignment and joint recovery of the slices in free-breathing and ungated cardiac cine MRI. The main highlights are
(1) the ability to align multi-slice data and capitalize on the redundancy between the slices.
(2) The ability to estimate the gating information directly from the k-t space data.
(3) The unsupervised learning strategy that eliminates the need for extensive training data.
The joint recovery facilitates the acquisition of data from the whole heart in around 2 minutes of acquisition time.
Purpose/Introduction
Self-gating methods are being widely used for free-breathing cine MRI [1]; these methods use k-space navigators to estimate the cardiac/respiratory phase, followed by the binning and recovery of measured data. Recently, manifold approaches including SToRM [2], which perform soft-gating based on k-space navigators are emerging as powerful alternatives to self-gating. All of these schemes perform the independent recovery of the slices in multislice acquisitions and hence fail to capitalize on the interslice redundancies.In this work, we propose a deep generative model for the alignment and joint recovery of slices in multi-slice cine MRI. This is the multislice generalization of the single slice generative SToRM approach in our companion abstract [1]. We represent the multislice volume at each time point as the output of a deep CNN generative network, which is driven by latent vectors that capture the cardiac and respiratory phase at the specific time point. Since the cardiac and respiratory motion during the acquisition of the different slices are different, we will use different latent vector time-series for each slice, while the generator will be the same for all volumes. The parameters of the generator and the latent time-series are jointly learned from the measured data of all the slices. Post recovery, the generator is excited using the latent variables of any slice, when it generates aligned multi-slice data with matching cardiac/respiratory phases. The proposed scheme is illustrated in Fig. 1.
Methods
The image volume at the time point $$$t$$$ during the acquisition of the $$$i^{\rm th}$$$ slice, denoted by $$$\rho(i,t)$$$ are represented as the non-linear mapping $$$\rho(i,t) = G_{\theta}(\mathbf{z}_{it})$$$. Here, $$$\mathbf{z}_{it}$$$ are the low (3-4) dimensional latent vectors corresponding to slice $$$i$$$ at a specific time point $$$t$$$, while $$$G_{\theta}$$$ is represented is a deep CNN generator, whose weights are denoted by $$$\theta$$$. Note that we use the same network for all the slices, which facilitates the exploitation of the spatial redundancies between the slices and is also memory efficient. We propose to jointly estimate the network parameters $$$\theta$$$ and the latent variables of the different slices from the measured multislice data as $$\mathcal C(\mathbf z,\theta)= \sum_{i=1}^M\sum_{t=1}^N\|\mathcal A_{it}\left(\mathcal G_{\theta}[\mathbf z_{it}]\right) - \mathbf b_{it}\|^2 + \lambda_1 \underbrace{\|\nabla_{\mathbf z} \mathcal G_{\theta}\|^2}_{\scriptsize \mbox{network regularization}} + \lambda_2 \underbrace{\|\nabla_{t} \mathbf z_t\|^2 }_{\scriptsize\mbox{temporal regularization}}.$$ Here, $$$A_{i,t}$$$ corresponds to the measurement operator, which extracts the $$$i^{\rm th}$$$ slice and evaluates its multichannel Fourier transform. We regularize the weights of the generator and apply a smoothness regularization of the latent vectors corresponding to different slices. The parameters are jointly learned in an unsupervised fashion from the measured k-t space data.Results
The proposed scheme is demonstrated on two datasets which were acquired on a GE 3T scanner. The sequence parameters are: TR = 8.4 ms, FOV = 320 mm x 320 mm, flip angle = 18, slice thickness = 8 mm. We consider the recovery from around 8 seconds of data/slice, which translates to 2.2 minutes of acquisition for the heart with 16 slices. Fig. 2 shows the reconstruction of four slices from the first dataset. Four different phases are shown in the figure and the corresponding latent vectors are given highlighted in the plot of the latent vectors. Fig. 3 shows the reconstruction of four slices from the second dataset and we also showed four different phases. This dataset is challenging due to extensive respiratory motion and hence we use latent variable of size 3 x 1 for the reconstruction, which is different from the scenario for the first dataset, where we use latent vector of size 2x1.Conclusion
The experiments show the potential of the proposed scheme in the reconstruction of free breathing and ungated cardiac MRI. This scheme does not require navigators for acquiring the data, which makes it more flexible for clinical scanners.Acknowledgements
This work is supported by NIH under Grants R01EB019961. This work was conducted on an MRI instrument funded by 1S10OD025025-01.References
[1] Feng et al, MRM 2014.
[2] Poddar et al., IEEE TMI 2016.
[3] Zou et al, ISMRM 2021.
Figures
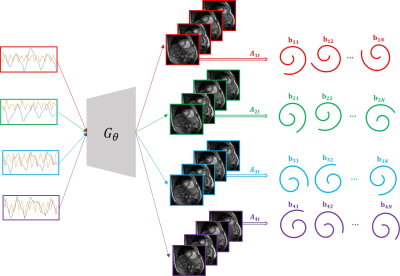
Fig. 1. Illustration of the scheme
with 4 slice cine dataset. The latent vectors are fed into the deep generative
model $$$\mathcal{G}_{\theta}$$$, which then generates the
multislice images in the time series. The figure shows the multislice images at a specific time $$$t$$$. The latent vectors and the parameters $$$\theta$$$ of the
generative model are learned from the measured k-t space data $$$b_{it}$$$ of the specific subject.
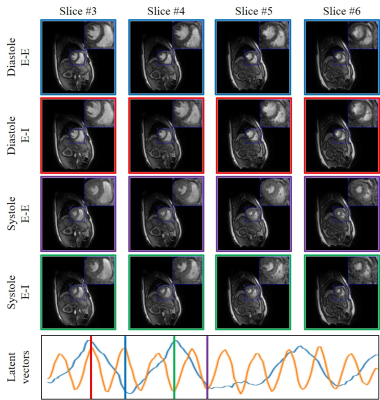
Fig.
2. Demonstration of the
framework of the proposed scheme on the first dataset. We plot the latent
variables of 150 frames in time series on the first dataset. We showed four
different phases from 4 different slices that are reconstructed in the time
series: systole in End-Expiration (E-E), systole in End-Inspiration (E-I),
diastole in End-Expiration (E-E) and diastole in End-Inspiration (E-I). The
latent vectors corresponding to the four different phases are indicated in the
plot of the latent vectors.
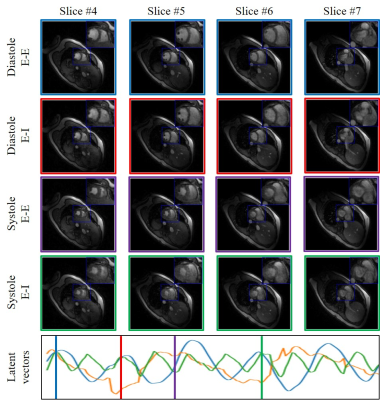
Fig. 3. Illustration of the framework of the proposed
scheme on the second dataset. We plot the latent variables of 150 frames in
time series on the first dataset. We showed four different phases from 4
different slices that are reconstructed in the time series: systole in
End-Expiration (E-E), systole in End-Inspiration (E-I), diastole in
End-Expiration (E-E) and diastole in End-Inspiration (E-I). The latent vectors
corresponding to the four different phases are indicated in the plot of the
latent vectors.
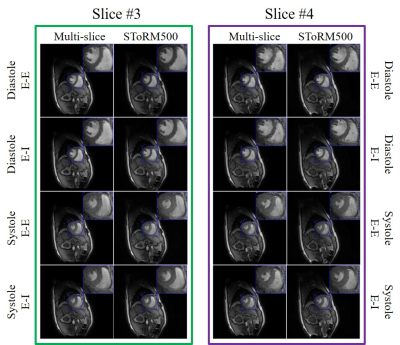
Fig. 4. Visual comparison with
SToRM method. SToRM500 corresponds to the reconstructions from 500 frames (~
25s of acquisition time) while the multi-slice (proposed) ones are recovered
from 150 frames (~ 7.5s of acquisition time). From the reconstructions, we can
see that the proposed scheme performs comparable to SToRM, even though the
proposed scheme uses only one-third of the data.