1956
Novel insights on SSA-FARY: Amplitude-based respiratory binning in self-gated cardiac MRI1Diagnostic and Interventional Radiology, University Medical Center Göttingen, Göttingen, Germany, 2Partner Site Göttingen, German Centre for Cardiovascular Research (DZHK), Göttingen, Germany
Synopsis
Cardiac MRI is challenging because of respiratory and cardiac motion. Current clinical approaches try to bypass motion-related issues by ECG-triggering and breath-holds, which comes with several drawbacks. Alternatively, self-gating techniques can be used to determine respiratory and cardiac motion from the acquired raw-data itself. We present novel insights on the quadrature-pair self-gating signals estimated by SSA-FARY: We show that one element of each pair is certain to be in-phase with the motion it represents, as it is the result of a filtering process with a zero-phase filter. This enables the use of less respiratory bins, which decreases the computational demand.
Introduction and Purpose
In cardiac MRI we have to account for cardiac and respiratory motion, which is usually done by ECG-triggering and breath-holds [1,2]. However, ECG-signals are error-prone when using fast-switching gradients [3] and patients might be incapable of performing breath-holds. A promising alternative is self-gated MRI, which dispenses with external devices or patient compliance by determining the respiratory and cardiac motion from the acquired data itself [4,5,6]. Recently, the SSA-FARY technique was proposed, which extracts cardiac and respiratory motion from the DC component of k-space and represents each quasi-periodic motion by quadrature pairs [7]. Here, we provide novel insights on the characteristics of these quadrature pairs: We show that one signal of each pair is generated by a zero-phase filter, for which it is in-phase with the actual physical motion and can therefore be used for amplitude-based respiratory binning. This kind of binning does not distinguish between inspiration and expiration - which in general is not ideal [7,8] - but can help to reduce the computational demand by allowing for a reduced number of bins in respiratory gating.Theory
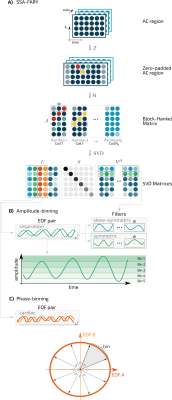
SSA-FARY is based on Singular Spectrum Analysis [9] and combines three basic and easy-to-implement mathematical operations to a powerful machine-learning technique for the extraction of quasi-periodic motion and trend contained in an auto-calibration (AC-)region. In radial imaging the center of k-space of each spoke can be used as AC-region. Furthermore, the real- and imaginary part of all channels, i.e. $$$N_\text{c}$$$ coils and $$$N_\text{p}$$$ partitions, are stacked to construct an AC-region $$$\boldsymbol{X}$$$ of size[$$$(2\times N_\text{c} \times N_\text{p})\times N_\text{t}$$$], with $$$N_\text{t}$$$ the number of time-steps [7]. Note, however, that SSA-FARY is not limited to radial imaging and any appropriate AC-region can be used.The three operations involved in SSA-FARY are (FIG_1A):
1. Zero-padding $$$\mathcal{Z}$$$
The AC-region $$$\boldsymbol{X}$$$ is symmetrically padded by $$$W - 1$$$ zeros to obtain
$$$\tilde{\boldsymbol{X}} = \mathcal{Z}\boldsymbol{X}$$$.
The odd window-size $$$W$$$ is chosen to capture ~3 seconds, which is the approximate time of a typical breathing cycle.
2. Hankelization $$$\mathcal{H}$$$
For each channel, a window of size [$$$1\times W$$$] is slided through the temporal domain and a Block-Hankel matrix $$$\boldsymbol{A}$$$ is constructed.
$$$\boldsymbol{A}=\mathcal{H}\tilde{\boldsymbol{X}}$$$.
3. Singular value decomposition SVD
The Block-Hankel matrix is decomposed using an SVD.
$$$\boldsymbol{A}=USV^H$$$
In [7,10] it was shown that the singular-vectors in $$$V^H$$$ contain $$$W$$$-sized data-adaptive filters for each channel, which act upon the zero-padded AC-region $$$\tilde{\boldsymbol{X}}$$$ to obtain the columns of $$$U$$$, also called Empirical Orthogonal Functions (EOF).
$$$U_t^k=\frac{1}{\lambda_k}\sum_{c=1}^{2 \cdot N_\text{c} \cdot N_\text{p}}\sum_{j=1}^{W}\tilde{\boldsymbol{X}}_c^{t+j}V_{cj}^k$$$
Like this, each oscillatory signal contained in the AC-region yields a pair of EOFs, which represent the desired gating signal. These EOFs are in quadrature and thus can be thought of as generalized sine-cosine pairs. Harris and Yuan [10] showed for the single-channel case, that for sufficiently large time-series, i.e. $$$N_\text{t}>>W$$$, one EOF of each quadrature pair is generated by a symmetric filter and one by a skew-symmetric filter, respectively (FIG_1B). In our experience, this also holds true for the multi-channel case. The consequence of this finding is remarkable:
The EOF generated by the symmetric (zero-phase) filter will always be in sync with the actual motion, as a zero-phase filter does not induce any phase-shift.
This property of the quadrature pairs allows for two different ways of sorting the acquired data according to their respiratory and cardiac phase:
1. Amplitude-binning (FIG_1B)
Amplitude-binning sorts the data acoording to the amplitude of the respective gating signal. For SSA-FARY, the in-phase EOF must be utilized, which can be detected by analysing the symmetry of the corresponding filters. Note, that amplitude-binning can be used for respiratory motion [11,12] but is not applicable for cardiac motion, as contraction and relaxation of the heart must be distinguished.
2. Phase-binning (FIG_1C)
Phase-binning resolves the entire cycle of a quasi-periodic motion by sorting the data according to the angle defined by the quadrature pair and can be used for both respiratory and cardiac gating [7].
Methods
We revisit the self-gating and reconstruction of the 1min radial 3-slice SMS-FLASH acquisition (TE/TR=1.79/2.90ms) described in [7]. Contrary to the publication, which utilizes SSA-FARY phase-binnig for both respiratory (9 bins) and cardiac motion (25 bins), we here use SSA-FARY amplitude-binning to sort the respiratory motion into 5 bins only. Multi-dimensional image reconstruction using BART [13] is performed as described in [7]. RING is used for gradient-delay correction [14].Results
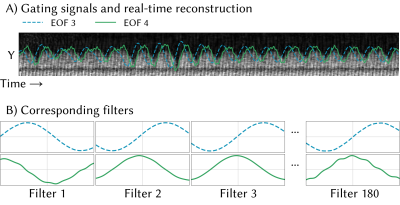
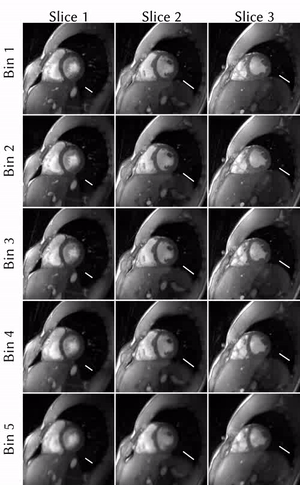
The background of FIG_2A shows the diaphragm motion extracted from a real-time reconstruction [15,16]. On top, the respiratory EOF-pair is plotted. For each EOF, FIG_2B shows 4 representative filters. Note, that the symmetric filters (green) correspond to the in-phase EOF in FIG_2A, which therefore was used for amplitude-binning.FIG_3 shows the cardiac cycle for all three slices resolved into 5 amplitude-binned respiratory states. The different depths of breathing can be appreciated considering the white reference lines.
Discussion and Conclusion
SSA-FARY can be used for robust respiratory and cardiac self-gating. To reduce the number of required bins for respiratory motion, amplitude-binning can be used by selecting the appropriate in-phase EOF of the quadrature pair. This approach was demonstrated on a radial SMS-FLASH acquisition and futhermore successfully tested in multiple other experiments (not shown).Acknowledgements
This work was supported by the German Centre for Cardiovascular Research (DZHK) and funded by the German Research Foundation (DFG) under Grant UE 189/1-1 and in part by NIH under grant U24EB029240.References
[1] C. B. Higgins and H. Hricak, Magnetic Resonance Imaging of the Body, Amsterdam, The Netherlands: Elsevier, 1987.
[2] Y. L. Liu et al. "A monitoring, feedback, and triggering system for reproducible breath-hold MR imaging" Magn. Reson. Med. 1993; 30:507–511.
[3] R. Rokey et al., "Monitoring of acutely III patients during nuclear magnetic resonance imaging: Use of a time-varying filter electrocardiographic gating device to reduce gradient artifacts", Magn. Reson.Med., vol. 6, no. 2, pp. 240-245, Feb. 1988.
[4] A. C. Larson, R. D. White, G. Laub, E. R. McVeigh, D. Li and O. P. Simonetti, "Self-gated cardiac cine MRI", Magn. Reson. Med., vol. 51, no.1, pp. 93-102, 2004.
[5] A. C. Larson et al., "Preliminary investigation of respiratory self-gating for free-breathing segmented cine MRI", Magn. Reson. Med., vol. 53, no. 1, pp. 159-168, Jan. 2005.
[6] S. Uribe et al., "Whole-heart cine MRI using real-time respiratory self-gating", Magn. Reson. Med., vol. 57, no. 3, pp. 606-613, Mar. 2007.
[7] S. Rosenzweig, et al. "Cardiac and Respiratory Self-Gating in Radial MRI Using an Adapted Singular Spectrum Analysis (SSA-FARY)", IEEE Trans. Med. Imag., vol. 39, no. 10, pp. 3029-3041, Oct. 2020.
[8] K. Nehrke et al., “Free-breathing cardiac mr imaging: study of implications of respiratory motion—initial results,” Radiology, vol. 220, no. 3, pp. 810–815, 2001.
[9] R. Vautard and M. Ghil, “Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series.” Phys. D, Nonlinear Phenomena, vol. 35, no. 3,pp. 395–424, 1989.
[10] T. Harris and H. Yuan, “Filtering and frequency interpretations of singular spectrum analysis”, Physica D, vol. 239, no. 20-22, pp. 1958–1967, 2010.
[11] L. Feng et al., “XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing”, Magn. Reson. Med., vol. 75, no. 2, pp. 775–788, 2016.
[12] J. Paul et al., “High-resolution respiratory self-gated golden angle cardiac MRI: comparison of self-gating methods in combination with k-t SPARSE SENSE”, Magn. Reson. Med., vol. 73, no. 1, pp. 292–298, 2015.
[13] M. Uecker et al. "Berkeley advanced reconstruction toolbox", In Proc. Intl. Soc. Mag. Reson. Med., vol. 23, p. 2486, 2015.
[14] S. Rosenzweig et al.“Simple auto-calibrated gradient delay estimation from few spokes using radial intersections (RING)”, Magn. Reson. Med., vol. 81, no. 3, pp. 1898–1906, 2019.
[15] M. Uecker et al. “Nonlinear inverse reconstruction for real-time MRI of the human heart using undersampled radial FLASH”, Magn. Reson. Med., vol. 63, no. 6, p. 1456–1462, 2010.
[16] S. Rosenzweig et al. “Simultaneous Multi-Slice Real-Time Imaging with Radial Multi-Band FLASH and Nonlinear Inverse Reconstruction”, in Proc. Intl. Soc. Mag. Reson.Med., vol. 24, p. 0518, 2017.
Figures