1954
Effective Training of 3D Unrolled Neural Networks on Small Databases1University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, Minneapolis, MN, United States
Synopsis
Unrolled neural networks have been shown to improve the reconstruction quality for accelerated MRI. While they have been widely applied in 2D settings, 3D processing may further improve reconstruction quality for volumetric imaging with its ability to capture multi-dimensional interactions. However, implementation of 3D unrolled networks is generally challenging due to GPU-memory limitations and lack of availability of large databases of 3D data. In this work, we tackle both these issues by an augmentation approach that generates smaller sub-volumes from large volumetric datasets. We then compare the 3D unrolled network to its 2D counterpart, showing the improvement from 3D processing.
INTRODUCTION
Deep learning (DL) has recently received significant interest for accelerated MRI reconstruction1-9. Among DL methods, the physics-guided approaches that rely on algorithm unrolling have shown to offer high-quality reconstructions with improved performance3. In these methods, iterative algorithms for solving a regularized least squares objective function, which alternate between data consistency and regularization, are unrolled for a fixed number of iterations. The regularization units are implemented via neural networks, while the data consistency is solved using standard linear methods. Most of the current unrolled networks use 2D convolutions1,2,5-7. 3D kernels have also been used in some studies, either through specialized training tools4 or simplified data consistency approaches8. Nonetheless, it remains challenging to train unrolled networks with 3D processing which has the potential to offer improved reconstruction quality compared to 2D processing due to both memory constraints of the GPUs and the lack of availability of large databases of 3D data.
In this work, we tackle these challenges for 3D training by generating multiple 3D slabs of smaller size from the full 3D volume. This enables both a data augmentation strategy for small database sizes, and a processing strategy for using the GPU memory without the need for specialized tools. We use this small-slab database to train a 3D unrolled network and compare it to its 2D counterpart with matched number of parameters, highlighting the advantages of 3D processing.
METHODS
3D Knee Data and Database Augmentation: Fully-sampled 3D knee datasets were obtained from mri-data.org10. The dataset consisted of 20 subjects, scanned at 3T (8-channel coil array) with FOV=160×160×154mm3, resolution=0.5×0.5×0.6mm3, matrix size = 320×320×256. Due to the small size of this database, training of a large unrolled network is prone to overfitting. Thus, from each full volume acquisition, we generated multiple smaller 3D slabs by taking the inverse Fourier transform along the fully-sampled read-out(kx) direction and dividing the volume to multiple slabs of size 20×320×256 (Fig. 1). 310 small slabs were generated from 10 subjects for training using this methodology.Unrolled Networks: MRI reconstruction from undersampled measurements is modeled as $$\arg\min_{\bf x}\|\mathbf{y}_{\Omega}-\mathbf{E}_{\Omega}\mathbf{x}\|^2_2+\cal{R}(\mathbf{x})$$
where x is the image of interest, $$$\mathbf{y}_{\Omega}$$$ is the acquired measurements with sub-sampling pattern $$$\Omega$$$ , $$$\mathbf{E}_{\Omega}$$$ is the multi-coil encoding operator, and $$$ \cal{R}(.)$$$ is a regularizer.There are multiple optimization algorithms for solving such objective functions, where a common theme is to decouple the DC and regularization to two separate sub-problems6. In unrolled networks, such conventional iterative algorithms are unrolled for a fixed number of iterations and the proximal operation of the regularizer is learned implicitly by neural networks (Fig. 2).
Training Details: The fully-sampled k-space data was retrospectively undersampled in the ky-kz plane with acceleration rate (R)=8 and ACS=32 using a sheared sampling pattern12. The 3D unrolled network comprised 5 unrolled blocks, each including a 3D ResNet9 architecture (3×3×3 convolutional kernels) with 5 residual blocks and a DC using a conjugate gradient approach2 that was also unrolled for 5 iterations and using warm start. A comparison was made by training a 2D unrolled network using the 2D slices generated from the full volume as training dataset. The 2D unrolled network also consisted of 5 unrolled blocks, and a DC unit with 5 unrolled CG iterations and warm start. It used a 2D ResNet9 architecture with 3×3 convolutions, but 15 residual blocks to match the number of trainable parameters in the 3D ResNet. Both unrolled networks were trained for 100 epochs with learning rate 5×10-4 using a normalized - loss function6. The reconstruction results were quantitatively evaluated using SSIM and NMSE.
RESULTS
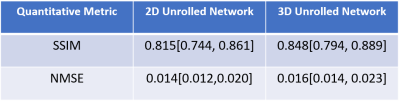
Fig. 3 shows 3D knee MRI reconstruction results for 2D and 3D processing at R = 8. 2D processing suffers from residual artifacts shown with red arrow. Proposed 3D processing achieves an improved reconstruction quality compared to 2D processing by further removing residual artifacts. Table 1 displays median and interquartile range (25th-75th percentile) of SSIM and NMSE values on the whole test dataset.DISCUSSION
In this work, we propose a 3D processing approach to tackle the data scarcity and GPU limitations for training 3D unrolled networks for volumetric reconstruction by generating small sub-volumes from large volumetric datasets. Results on knee MRI show that the proposed training performed on just data from 10 subjects achieves improved reconstruction quality compared to its 2D processing counterpart. When large datasets are processed, specialized training tools4 can also be applied to assist the improvement of reconstruction results. Our strategy for data augmentation may extend the utility of such tools to even higher dimensional processing. In addition, self-supervised training may also be employed when ground truth is not be available in some 3D scans9.CONCLUSIONS
In this work, we propose a data augmentation strategy that uses smaller sub-volumes from large 3D MRI datasets to tackle two problems for the training of 3D unrolled networks, and show such networks outperform their 2D counterparts.Acknowledgements
Grant support: NIH R01HL153146, NIH P41EB027061, NIH U01EB025144; NSF CAREER CCF-1651825References
1. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine, 2018, 79(6): 3055-3071.
2. Aggarwal H K, Mani M P, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 2018, 38(2): 394-405.
3. Knoll F, Murrell T, Sriram A, Yakubova N, Zbontar J, Rabbat M, Defazio A, Muckley MJ, Sodickson DK, Zitnick CL, Recht MP. Advancing machine learning for MR image reconstruction with an open competition: Overview of the 2019 fastMRI challenge. Magn Reson Med 2020;84(6):3054-3070. 4. Kellman M, Zhang K, Markley E, et al. Memory-efficient learning for large-scale computational imaging. IEEE Transactions on Computational Imaging, 2020, 6: 1403-1414.
5. Hosseini S A H, Yaman B, Moeller S, et al. Dense recurrent neural networks for accelerated mri: History-cognizant unrolling of optimization algorithms. IEEE Journal of Selected Topics in Signal Processing, 2020, 14(6): 1280-1291.
6. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Uğurbil K, Akçakaya M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn Reson Med 2020;84(6):3172-3191.
7. Knoll F, Hammernik K, Zhang C, et al. Deep-learning methods for parallel magnetic resonance imaging reconstruction: A survey of the current approaches, trends, and issues. IEEE Signal Processing Magazine, 2020, 37(1): 128-140.
8. Küstner T, Fuin N, Hammernik K, et al. CINENet: deep learning-based 3D cardiac CINE MRI reconstruction with multi-coil complex-valued 4D spatio-temporal convolutions. Scientific reports, 2020, 10(1): 1-13.
9. Yaman B, Shenoy C, Deng Z, et al. Self-Supervised Physics-Guided Deep Learning Reconstruction For High-Resolution 3D LGE CMR. arXiv preprint arXiv:2011.09414, 2020.
10. Ong F, Amin S, Vasanawala S, Lustig M. Mridata. org: An open archive for sharing MRI raw data. Proceedings of the 26th Annual Meeting of ISMRM.
11. Fessler J A. Optimization methods for magnetic resonance image reconstruction: Key models and optimization algorithms. IEEE Signal Processing Magazine, 2020, 37(1): 33-40.
12. Breuer F A, Blaimer M, Mueller M F, et al. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 2006, 55(3): 549-556.
Figures