1953
Scalable and Interpretable Neural MRI Reconstruction via Layer-Wise Training
Batu Ozturkler1, Arda Sahiner1, Mert Pilanci1, Shreyas Vasanawala2, John Pauly1, and Morteza Mardani1
1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States
1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States
Synopsis
Deep-learning based reconstruction methods have shown great promise for undersampled MR reconstruction. However, their lack of interpretability, and the nonconvex nature impedes their utility as they may converge to undesirable local minima. Moreover, training deep networks in high-dimensional imaging applications such as DCE, and 4D flow requires large amounts of memory that may overload GPUs. Here, we advocate a layer-wise training method amenable to convex optimization, and scalable for training 3D-4D datasets. We compare convex layer-wise training to traditional end-to-end training. The proposed method matches the reconstruction quality of end-to-end training while it is interpretable, convex, and demands less memory.
Introduction
Recently, deep-learning (DL) based approaches emerged for accelerated MRI, often surpassing traditional methods such as compressed sensing [12] and parallel imaging [13] in diagnostic image quality [1-3]. Current DL algorithms rely on model-based image reconstruction, where an iterative algorithm involving a CNN-based regularizer is unrolled and trained end-to-end [4-6].However, there are three main limitations of these networks: (i) the black-box nature of neural networks limit their trust in clinical practice, (ii) the non-convex nature of training may trap the training into undesirable local minima and lack stability guarantees [7], and (iii) since unrolled networks are trained end-to-end, the number of unrolled iterations is constrained by GPU memory, thus limiting the expressivity of these networks. As a result, unrolled networks are infeasible for reconstruction in high-dimensional imaging applications such as 4D flow and DCE abdominal imaging.
Motivated by these challenges, we put forth a novel layer-wise training framework, where the training problem for each layer is convex, and is guaranteed to find the global optimum of the training problem. Furthermore, each training step requires less GPU memory compared to end-to-end training, making high-dimensional imaging applications of deep networks feasible.
Theory
Two-layer fully-convolutional denoising networks, consisting of a convolution with arbitrary kernel size, ReLU, and a 1x1 convolution with a skip connection were shown to be amenable to convex optimization in our companion work [8]. Here, we use these networks to construct deep reconstruction networks with higher expressivity via “layer-wise training”. Layer-wise training of shallow networks has been shown to achieve comparable performance with end-to-end training of deep networks in image classification tasks [9]. Layer-wise training is performed sequentially for each layer, whereas in end-to-end training, all layers are trained jointly using back-propagation.Let the predictions of the $$$i^{th}$$$ two-layer network be $$$\hat{x_i} = f_i(g_i(x_i)_+)+x_i$$$, where $$$g_i$$$ is the first layer, $$$f_i$$$ is the second layer, $$$(.)_+$$$ is ReLU, $$$x_i$$$ is the input of $$$i^{th}$$$ layer, and $$$i = 1,..,k$$$ for a $$$k+1$$$ layer network. At $$$i^{th}$$$ training step, a two-layer network from [8] is trained to fit the ground-truth using $$$l_2$$$ loss. After training has finished, $$$f_i$$$ is removed, and the $$$(i+1)^{th}$$$ two-layer network is trained. This training algorithm is repeated $$$k$$$ times to obtain a deep network with $$$k+1$$$ layers. The proposed training algorithm is illustrated in Figure 1.
Methods
We adopt the fastMRI multi-coil knee dataset [11] for evaluation where the acquisition is a Cartesian 2D FSE sequence. 30 subjects are used for training, while 6 subjects are used for validation. The resolution of each slice is 320x320, and the number of coils is 15. The inputs to the network are zero-filled images obtained with SENSE [10] reconstruction with a calibration region of 16x16. The network fits the zero-filled image to the target image, where each complex-valued image is a two-channel tensor representing real and imaginary components.We compared our method with end-to-end training. We considered two scenarios for evaluation under different undersampling trajectories: Poisson disc sampling and 1D Cartesian sampling with 0.04 center fraction, both at 4x undersampling rate. We used slice-based PSNR and SSIM as our evaluation metrics. Training was performed in PyTorch with ADAM optimizer [14] on a single GPU with 12 GB of memory. Networks were trained for 40 epochs for Poisson Disc mask sampling and 30 epochs for 1D Cartesian sampling, with a learning rate of $$$10^{-4}$$$, and learning rate was reduced by 2 every 10 epochs.
Results
Convex layer-wise training achieved on par performance with end-to-end training for both settings (Fig. 2). For Poisson disc sampling and 1D Cartesian sampling, the PSNR gap was 0.06 dB and 0.3 dB, and the SSIM gap was 0.002 and 0.003 respectively. Representative images from the test set are demonstrated in Figure 3. Both methods mitigated blurring artifacts for Poisson Disc mask sampling and aliasing artifacts for 1D Cartesian sampling, producing high-fidelity reconstruction with similar image quality.In addition, layer-wise training allows for more than 60% higher batch size than end-to-end training (Fig. 4): gradients are calculated for a two-layer network at each training step, allowing for a smaller memory footprint. This suggests that layer-wise training can enable training with high-dimensional datasets.
Discussion
While convex layer-wise training matches the performance of end-to-end training, it offers several advantages. Layer-wise training uses two-layer networks, which can be interpreted as piecewise linear filtering [8]. In contrast to non-convex models, convergence of the proposed convex algorithm is independent of optimizer hyperparameters such as initialization or batch-size, and thus requires less tuning. Given its interpretability and stability guarantees through convexity, layer-wise training can facilitate safe deployment of DL algorithms for clinical applications. Moreover, convex layer-wise training can scale DL algorithms for applications such as 3D cardiac cine that require large-scale networks with 3D convolutions, which are difficult to train end-to-end due to memory limitations. The proposed algorithm provides flexibility to select hyperparameters such as regularization for each layer separately, which may allow better generalization compared with end-to-end training.Conclusion
We presented convex layer-wise training, a scalable and interpretable training algorithm that provides convergence guarantees for large-scale networks without compromising performance compared to end-to-end training.Acknowledgements
We would like to acknowledge support from R01EB009690, U01EB029427, R01EB026136, and GE Healthcare.References
- Morteza Mardani, Enhao Gong, Joseph Y Cheng, Shreyas S Vasanawala, Greg Zaharchuk, Lei Xing, and John M Pauly. Deep generative adversarial neural networks for compressive sensing mri. IEEE transactions on medical imaging, 38(1):167–179, 2018.
- Kerstin Hammernik, Teresa Klatzer, Erich Kobler, Michael P Recht, Daniel K Sodickson, Thomas Pock, and Florian Knoll. Learning a variational network for reconstruction of accelerated mri data. Magnetic resonance in medicine, 79(6):3055–3071, 2018.
- Guang Yang, Simiao Yu, Hao Dong, Greg Slabaugh, Pier Luigi Dragotti, Xujiong Ye, Fangde Liu, Simon Arridge, Jennifer Keegan, Yike Guo, et al. Dagan: Deep de-aliasing generative adversarial networks for fast compressed sensing mri reconstruction. IEEE transactions on medical imaging, 37(6):1310–1321, 2017.
- Christopher M Sandino, Joseph Y Cheng, Feiyu Chen, Morteza Mardani, John M Pauly, and Shreyas S Vasanawala. Compressed sensing: From research to clinical practice with deep neural networks: Shortening scan times for magnetic resonance imaging. IEEE Signal Processing Magazine, 37(1):117–127, 2020.
- Hemant K Aggarwal, Merry P Mani, and Mathews Jacob. Modl: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 38(2):394–405, 2018.
- Y. Yang, J. Sun, H. LI, and Z. Xu. ADMM-CSNet: A Deep Learning Approach for Image Compressive Sensing. IEEE Transactions on Pattern Analysis and Machine Intelligence, IEEE Computer Society, 2018.
- Vegard Antun, Francesco Renna, Clarice Poon, Ben Adcock, and Anders C Hansen. On instabilities of deep learning in image reconstruction and the potential costs of ai. Proceedings of the National Academy of Sciences, 2020
- Sahiner, A., Mardani, M., Ozturkler, B. M., Pilanci, M., Pauly, J. “Convex Regularization Behind Neural Reconstruction” https://arxiv.org/abs/2012.05169
- Belilovsky, E., Eickenberg, M. & Oyallon, E.. (2019). Greedy Layerwise Learning Can Scale To ImageNet. Proceedings of the 36th International Conference on Machine Learning, in PMLR 97:583-593
- K. P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger, “SENSE: Sensitivity encoding for fast MRI,” Magn. Reson. Med., 1999.
- Jure Zbontar, Florian Knoll, Anuroop Sriram, Matthew J. Muckley, Mary Bruno, Aaron Defazio,Marc Parente, Krzysztof J. Geras, Joe Katsnelson, Hersh Chandarana, Zizhao Zhang, MichalDrozdzal, Adriana Romero, Michael Rabbat, Pascal Vincent, James Pinkerton, Duo Wang,Nafissa Yakubova, Erich Owens, C. Lawrence Zitnick, Michael P. Recht, Daniel K. Sodickson, and Yvonne W. Lui. fastmri: An open dataset and benchmarks for accelerated MRI. CoRR, abs/1811.08839, 2018. URL http://arxiv.org/abs/1811.08839.
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195. doi:10.1002/mrm.21391
- M. Murphy, M. Alley, J. Demmel, K. Keutzer, S. Vasanawala, and M. Lustig. Fast ℓ1-SPIRiT compressed sensing parallel imaging MRI: Scalable parallel implementation and clinically feasible runtime. IEEE Trans Med Imaging. 2012;31(6):1250-1262. doi:10.1109/TMI.2012.2188039
- Kingma, D. P. & Ba, J. (2014), Adam: A Method for Stochastic Optimization arxiv:1412.6980
Figures
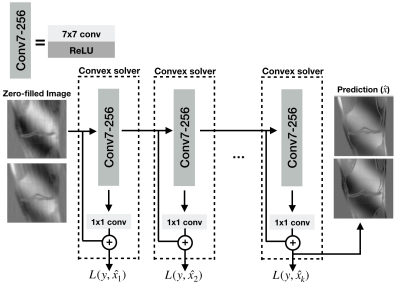
The proposed layer-wise training algorithm. At each training step, a two-layer network is trained to fit the ground-truth. After training has finished, the weights of the first layer are frozen, and the second training step is performed. This training algorithm is repeated k times to obtain a deep network with k+1 convolutional layers. L(y,$$$\hat{x}_i$$$) is the loss for ith step where y is ground-truth, and $$$\hat{x}_i$$$ is the prediction of ith layer. In the final network, each layer except the final layer have 7x7 kernel size and 256 channels, and the final layer has 1x1 kernel size.
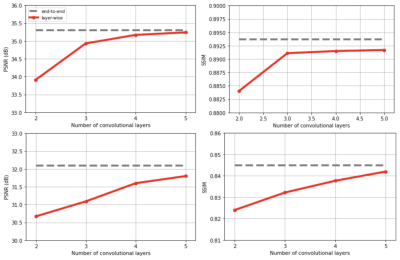
Test performance for convex layer-wise training vs end-to-end training with Poisson Disc sampling (top) and Cartesian sampling (bottom). For layer-wise training 5 layers are sequentially added. The same end-to-end network is trained also with end-to-end training. The gap between layer-wise and end-to-end training is negligible.
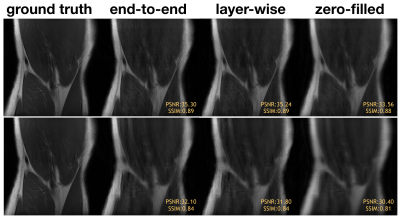
Representative knee images from the test set for layer-wise training vs end-to-end training with Poisson disc sampling (top) and Cartesian sampling (bottom). End-to-end training and layer-wise training have similar perceptual quality.

Maximum batch size of layer-wise training and end-to-end training allowed by memory constraints of a single GPU, with 256 convolutional filters and a 5-layer network. Layer-wise training allows for much higher batch sizes.