Introduction

Deep leaning-based reconstruction methods have shown great promise in undersampled MRI reconstruction^1–6. Joint optimization of the undersampling pattern and the reconstruction network using deep learning was reported to be able to further improve the reconstruction quality^7–9. However, previous works focused largely on static MRI. Here, we investigate this strategy on dynamic MRI. In particular, the use of convolutional recurrent neural network (CRNN), temporal degree of freedom (DoF) in learning-based sampling pattern, and k-space data sharing strategy in dynamic contrast-enhanced (DCE) MRI were investigated.

Methods

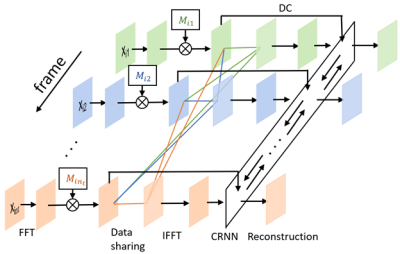
The neural network (figure 1) is divided into two parts. The first one is the sampling pattern optimization part, where we assign a 2D sampling probability mask for each temporal frame of the DCE MRI images. The second part is the DCE MRI image reconstruction part, where the CRNN framework² is used to explore the temporal correlations in MRI sequences. The dynamic images were retrospectively undersampled by the binary sampling pattern as a realization of the independent random variables with Bernoulli distribution defined by the learned probability masks as in LOUPE⁷. The images were then reconstructed using CRNN with 1 bidirectional convolutional recurrent neural network (BCRNN), 4 convolutional layers and 5 iterations. To further leverage the temporal redundancies in DCE MRI, a data sharing strategy, a probability including the k-space data from other frames in each frame, was learned jointly with the sampling pattern and the reconstruction network.
The learning objective can be formulated as the following:
$$ \arg\max_{\boldsymbol{p}, \Theta, \boldsymbol{p}_s} \sum_i \sum_{j=1}^{n_t} \|f_\Theta(F^H(M_{ij}F\mathbf{x}_{ij}+(1-M_{ij})\mathbf{k}_{s_{ij}}))-\mathbf{x}_{ij}\|_2^2+\max(0,\frac{\sum_{j=1}^{n_t}\sum_{l}\mathbf{p}_{jl}}{n_t}-R)+\lambda\mathcal{R}(\mathbf{p}) \tag{1}$$
$$\mathbf{k}_{s_{ij}}=\sum_{j'=1,j'\neq j}^{n_t}m_{jj'}M_{ij'}F\mathbf{x}_{ij'}/\sum_{j'=1,j'\neq j}^{n_t}m_{jj'}M_{ij'}\mathbf{1} \tag{2}$$
$$M_{ij}=diag(\mathbf{1}_{\mathbf{u}_{ij}\leq\mathbf{p}_{j}}), m_{jj'}=1_{\mathbf{u'}_{jj^\prime}\leq\mathbf{p}_{s_{jj^\prime}}} \tag{3}$$
where $$$\mathbf{x}_{ij}\in\mathbb{C}^{n_x n_y}$$$ is the MR image for the ith scan at frame j (with a total of frames), $$$F$$$/$$$F^H$$$ is the forward/inverse discrete Fourier transform matrix, $$$\mathbf{p}_{j}\in\mathbb{R}^{n_x n_y}$$$ is the vectorized 2D sampling probability mask for frame j, $$$\mathbf{p}_{s_{jj'}}\in\mathbb{R}$$$ is the probability of including the k-space data of frame j’ for the reconstruction of frame j, $$$\mathbf{u}_{ij}\in\mathbb{R}^{n_x n_y}$$$ and $$$\mathbf{u}_j^\prime\in\mathbb{R}^{n_t}$$$ are realizations of random vectors with independent uniform distribution on $$$[0,1)$$$, $$$f_\Theta(\cdot)$$$ denotes the reconstruction network parameterized by $$$\Theta$$$, $$$\mathbf{k}_{s_{ij}}$$$ is the k-space data shared by the other frames for the reconstruction of frame j of scan i, R is the acceleration factor of undersampling. For the data sharing process, if more than one data points are sampled at the same k-space location in the frames included for data sharing, an average is taken for that location (represented by the denominator of equation (2)). $$$\boldsymbol{p}, \Theta, \boldsymbol{p}_s$$$ are jointly optimized to minimize the l₂ norm between the reconstructed image and the ground truth. The second term of equation (1) allows the explicit control of the average acceleration factor without hyperparameter finetuning. $$$\mathcal{R}(\mathbf{p})$$$ denotes the regularization term on the sampling probability masks. A sigmoid function was used to approximate the indicator function.
DCE MR images were acquired from 30 patients with head and neck cancers using a 3D dynamic scanning sequence (TWIST) on a 3 Tesla MRI scanner (Skyra, Siemens Healthineers, Erlangen Germany). Of 30 patients, 20 patients were randomly selected for training, 5 for validation, and 5 for testing. Each patient scan had 60 time frames and 35 96×96 axial slices for each frame. Since magnitude images were used, during training, a uniformly distributed random phase in [0º, 10º) was added to k-space data to create the small phase variation.
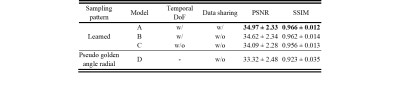
We investigated effects of leaning-based sampling pattern, temporal DoF for sampling pattern and data sharing. We compared different models with or without a temporal DoF and with or without learned data sharing. We also compared them with pseudo golden angle radial sampling without data sharing. By adding a temporal DoF, $$$\mathbf{p}_{j}$$$ of each time frame can be different. Otherwise, $$$\mathbf{p}_{j}$$$ is the same for all frames. R = 9.4 was used for all experiments.
The structural similarity index measure (SSIM) and peak signal to noise ratio (PSNR) were used as evaluation metrics.

Results

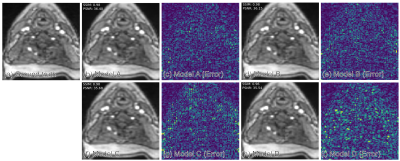
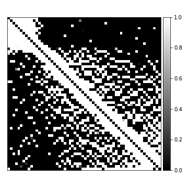
Table 1 compares the quantitative reconstruction quality of different models. The CRNN reconstruction network that was jointly trained for sampling patterns with a temporal DoF and learned data sharing (model A) shows the best performance. Exemplary reconstruction results of an image frame are shown in figure 2. The sampling probability maps of model A are shown in figure 3. In the later stage of training, the probability maps became almost deterministic with the probability values approaching either 0 or 1. The sampling probability masks of the first and last few frames appear more concentrated in the center of k-space. The data sharing probability map of model A is shown in figure 4. Different spreads of data sharing probabilities can be noticed for different frames.

Discussion and conclusion

This work combines CRNN, learning-based sampling pattern, and k-space data sharing for DCE MRI reconstruction. We explored the possibility of adding a temporal DoF to the sampling pattern and learning-based data sharing, which achieved better reconstruction results. The different spreads of probability in data sharing (figure 4) is possibly related to the pharmacokinetics of the contrast agent (CA). The MR images before, during, and after the CA uptake show high correlations, leading to high data sharing probabilities among the frames within each stage of contrast uptake.

Acknowledgements

No acknowledgement found.