Introduction

MRI is intrinsically slow due to physical and physiological limitations. Deep learning-based image reconstruction methods like the convolutional neural network have been demonstrated for dynamic MRI, providing new opportunities for fast and high-quality reconstruction. In comparison to flat convolution neural networks, the concatenation of several-element U-net is a more flexible model that works across different scales and shows outstanding performance, especially when operating in both image and k-space domains¹.

However, the reconstruction of dynamic MRI is inherently limited to model geometric transformations due to the fixed geometric structures of the convolution kernels, often leading to over smoothing artifacts. Deformable convolution, a novel convolution method used in computer vision tasks such as object detection and video deblurring, augments the spatial sampling locations in the modules with additional offsets^2-4. Deformable convolution kernels naturally adapt to image structures and could effectively reduce the blurring.

In this study, we aimed to demonstrate that deep learning-based dynamic image reconstruction can benefit from the incorporation of deformable convolution. We used cascaded U-net and replaced the standard convolution layer which extracts the feature of the input. The proposed method was compared against the zero-filling method, compressed sensing, standard cascaded U-net, and the fully-sampled reference.

Theory and Methods

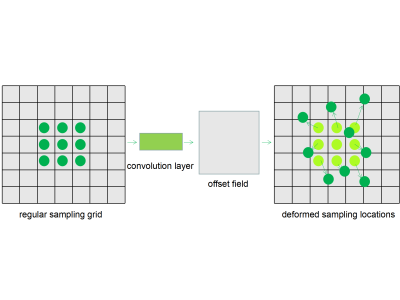
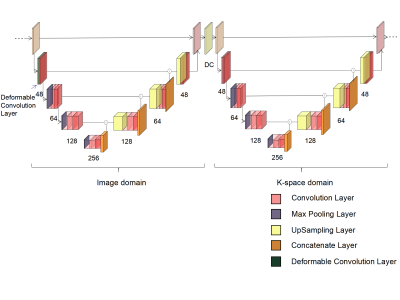
Deformable Convolution: In normal convolution with fixed uniform convolution kernels, each location $$$p_0$$$ on the output feature map $$$y$$$ is the summation of sampled values over the input feature map $$$x$$$ using a regular grid $$$R$$$ weighed by $$$w$$$ and we have $$$y(p_0)=\sum\limits_{p_n \in R}w(p_n)\cdot x(p_0+p_n)$$$. In deformable convolution, the regular grid is augmented with offsets and the feature map is computed as $$$y(p_0)=\sum\limits_{p_n \in R}w(p_n)\cdot x(p_0+p_n+\Delta p_n)$$$. The offsets are derived from the additional convolution layers over preceding feature maps, illustrated in Figure 1. Because the offsets are usually fractional, bilinear interpolation is used to sample the pixels. With deformable convolution, we replaced the normal convolution at the first convolution layer at every U-net block that operates in the image domain.

Network Architecture: Our models comprise cascading U-net where each U-net block operates either on k-space or image domains, following each other in the whole network. Figure 2 shows a cascaded U-net termed IK W-net composed of two blocks operating in the image domain and then the k-space domain. Every U-net block takes an undersampled k-space as input. If the block operates in the image domain, inverse Fourier transform is performed to turn the k-space input into low-resolution images. Each block has 22 convolution layers, three max-pooling layers, three up-sampling layers, and one residual connection. The convolution kernel sizes are 3 x 3. As is described in Roberto et al¹, four potential types of cascaded U-net were tested: a) W-net IK, b) WW-net IKIK, c) WWW-net IKIKIK. We carried out data consistency for the k-space at the end of each U-net block with updated k-space as output, and this data consistency implementation was a noiseless setting. The loss function used to train the model was the mean squared error.

Training: The network was trained on 2D images obtained from retrospectively undersampled CINE data of 5 subjects. The public data set was downloaded from https://www.kaggle.com/c/second-annual-data-science-bowl/data. The retrospective undersampled data were generated from variable-density sampling along the phase encoding dimension with acceleration factor $$$R=2$$$, $$$R=4$$$, and $$$R=8$$$.

Results and Discussion

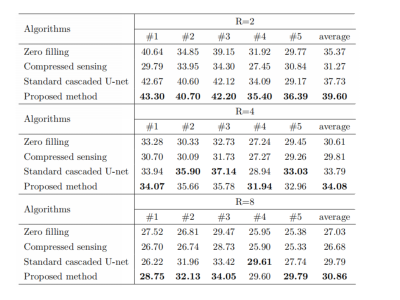
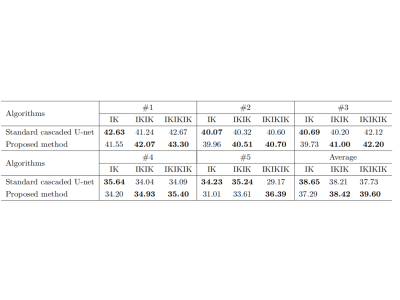
Table 1 shows the peak signal-to-noise ratio (PSNR) of cascaded IKIKIK U-net with deformable convolution under the circumstances of different acceleration factors and we compared it with standard cascaded U-net, compressed sensing with temporal total variation, and zero-filling. For acceleration factor R = 2, 4, and 8, the PSNR of images reconstructed by the proposed method was 39.60, 34.08, and 30.86, respectively, which were higher than other methods in the same condition. On average, cascaded IKIKIK U-net with deformable convolution achieved consistently better results.

Table 2 demonstrates the influence of network depth on the performance of deformable convolution. Multiple derivations of offset fields helped the improvement of output. Cascaded U-net with deformable convolution achieved better results as the depth increased. Judging from the average PSNR, increasing depth did not result in better images with standard cascaded U-net, but generated images of higher quality with the proposed method.

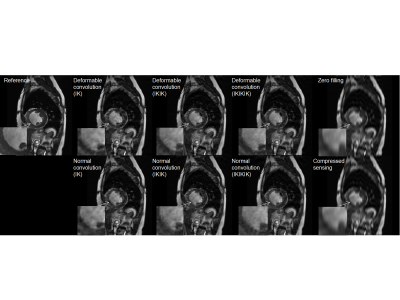
Figure 3 compares the output of a single frame reconstructed by multiple types of cascaded network. The acceleration factor here was 8. In comparison to standard cascaded U-net, the deformable convolution led to better results of deblurring especially on the ventricular wall where motion is highly significant.

Conclusion

We proposed to leverage the motion information in dynamic MRI by incorporating deformable convolution into cascaded U-net. The deformable convolution layers learn the offset field for the sampling of convolution kernels. The deformable convolution helps improve the reconstruction performance by alleviating over smoothing artifacts. As more U-net block is added to the network, the proposed method obtains better results with increasing exploitation of the offset field. The next step is to extend the deformable convolution into 3D (2D+t) offset field with varying numbers of sampling points in each frame, therefore more information can be sampled in reliable frames.

Acknowledgements

No acknowledgement found.