1946
A Plug-and-play Low-rank Network Module in Dynamic MR Imaging1Shenzhen Institutes of Advanced Technology, Shenzhen, China, 2University at Buffalo, The State University of New York, Buffalo, NY, United States
Synopsis
Accelerated dynamic MR Imaging is a significant but challenging task. Our previous work demonstrated that deep low-rank priors could achieve improved reconstruction performance by unrolling a sparse and low-rank-based optimization algorithm. However, the optimization algorithm is highly customized, and currently, no deep learning methods exist to apply low-rankness as prior to general inverse problems. In this paper, we propose a plug-and-play low-rank network module in dynamic MR imaging. The low-rank network module can be easily embedded into other deep learning models. The embedding of the LR module can effectively improve the reconstruction results.
Introduction
It is crucial to improve the temporal and spatial resolution of cardiac MR imaging by using fast imaging method without sacrificing image quality. As an extension of compressed sensing (CS) methods [1-3], low-rank priors [4-7] have been applied to dynamic MRI. By considering each temporal frame as a column of a space-time matrix, the low-rank prior from the spatio-temporal correlations of dynamic MR images was pursued by minimizing the number of non-zero singular values of this matrix. These methods could obtain improved reconstruction by suppressing the singular vectors of the low-rank matrix that correspond to artifacts and noise. Recently, deep learning (DL) has been introduced to speed up dynamic MR reconstruction [8-10]. For example, DIMENSION [10] developed a multi-supervised network training technique to simultaneously constrain frequency domain information and spatial domain information. These DL-based methods unroll sparse driven optimization into neural networks [10], while the low-rank priors have not been used in these DL methods. In our previous work [11], we proposed a learned low-rank prior and introduce it into a model-based unrolling deep network architecture, dubbed as SLR-Net. SLR-Net was defined over a deep network flow graph, which is unrolled from the iterative procedures in the iterative shrinkage-Thresholding algorithm (ISTA) for optimizing a sparse and low-rank based dynamic MRI model. Although experimental results showed that the proposed scheme could improve the reconstruction results, the highly customized optimization prevents its further popularization in other methods. We come up with a plug-and-play low-rank network module to benefit general dynamic imaging problems in this work. This plug-and-play LR network module can be easily embedded into any sparsity-driven deep learning models such as DC-CNN [8], CRNN [9], ISTA-Net [12] without changing the network paradigm.Theory and method
In SLR-Net [11], the low-rank prior of dynamic data has been introduced by unrolling a sparse and low-rank based optimization algorithm. In particular, the low-rank constrained sub-problem can be described as follows:$$t^n=\arg\min_t\ \frac{\rho}{2}||x^n+\beta^{n-1}-t||_2^2+\lambda_2||t||_*\ \ \ \ \ \ \ \ \ \ (1)$$
IST [13] is used to solve this nuclear norm minimization with a hard threshold scheme, and the proposed low-rank network module can be obtained:
$$
\begin{cases}
x^{n}&=U\Sigma V^*\\ t^n&=UH_k(\Sigma)V^*, \\ H_k(\Sigma) &= \text{diag}(\{\Sigma_i\}_{1\leq i\leq k})
\end{cases} \ \ \ \ \ \ \ \ \ \ (2)
$$
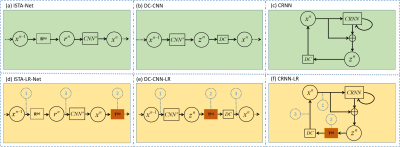
However, in SLR-Net [11], the optimization algorithm is highly customized. In this work, we treat the low-rank module as a plug-and-play block in this work, which can be easily embedded into other deep learning models without changing the network paradigm. This paper provides three instances of embedding the proposed learned LR module as shown in Fig.1. Fig.1 (a, b, c) represents the original ISTA-Net, DC-CNN, and CRNN, respectively. Fig.1 (d, e, f) represent their respective models embedded with the plug-and-play LR module, which is dubbed as ISTA-LR-Net, DC-CNN-LR CRNN-LR, respectively. The learned LR module performs SVT operations on the input signal as shown in Eq.2. If the LR module is embedded before the CNN network (L1), the low-rank prior are loaded into the dynamic signal, and the network will learn the sparse and low-rank features of the signal. If the LR module is embedded after the CNN network (L2, L3), the LR module is used for low-rank correction of predicted results to ensure its low-rank prior. The embedded LR module implies that the model favors the low-rank solution.
Experiment
The fully sampled cardiac cine data were collected from 30 healthy volunteers on a 3T scanner (MAGNETOM Trio, Siemens Healthcare, Erlangen, Germany) with a 20-channel receiver coil array. The following sequence parameters were used: FOV = 330*330 mm, acquisition matrix = 256*256, slice thickness = 6 mm, and TR/TE = 3.0 ms/1.5 ms. Each frame's raw multi-coil data were combined by an adaptive coil combine method [14] to produce a single-coil complex-valued image. We obtained 1548 2D-t cardiac MR data for training and 45 data for testing. The models have implemented on an Ubuntu 16.04 LTS (64-bit) operating system equipped with an Intel Xeon E5-2640 CPU and a Tesla TITAN Xp GPU. The open framework TensorFlow was used.Results
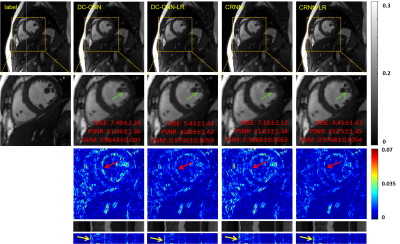
To demonstrate the efficacy of the proposed plug-and-play LR module, we embedded it in the state-of-the-art CNN-based DC-CNN [8], and CRNN [9] methods at location numbered 2 (L2). The reconstruction results of CNN-LR at 8-fold acceleration are shown in Fig.2. It is obvious that by embedding the LR module, the reconstruction results exhibit more details (as shown in the green arrow), and the smoothness is eliminated. The quantitative evaluations were also provided. All three performance metrics were significantly improved (DC-CNN: 2.0e-5 lower in MSE, 1.4dB higher in PSNR, and 0.009 higher in SSIM. CRNN: 2.7e-5 lower in MSE, 2.1dB higher in PSNR and 0.01 higher in SSIM). Both qualitatively and quantitatively, the plug-and-play low-rank prior achieves superior reconstruction performance.Conclusion
This paper explores a plug-and-play low-rank network module in dynamic MR imaging to obtain improved reconstruction results. It can be easily embedded into any other dynamic MR neural networks without changing the neural network paradigm. Experimental results show that the proposed plug-and-play low-rank module can improve the reconstruction results qualitatively and quantitatively.Acknowledgements
This work was supported in part by the National Key R&D Program of China (2020YFA0712202, 2017YFC0108802 and 2017YFC0112903); National Natural Science Foundation of China (61771463, 81830056, U1805261, 81971611, 61871373, 81729003, 81901736); Natural Science Foundation of Guangdong Province (2018A0303130132); Shenzhen Key Laboratory of Ultrasound Imaging and Therapy (ZDSYS20180206180631473); Shenzhen Peacock Plan Team Program (KQTD20180413181834876); Innovation and Technology Commission of the government of Hong Kong SAR (MRP/001/18X); Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000)References
[1]. Jung, Hong, Jong Chul Ye, and Eung Yeop Kim. "Improved k–t BLAST and k–t SENSE using FOCUSS." Physics in Medicine & Biology 52, no. 11 (2007): 3201.
[2]. Lingala, Sajan Goud, Yue Hu, Edward DiBella, and Mathews Jacob. "Accelerated dynamic MRI exploiting sparsity and low-rank structure: kt SLR." IEEE transactions on medical imaging30, no. 5 (2011): 1042-1054.
[3]. Otazo, Ricardo, Emmanuel Candès, and Daniel K. Sodickson. "Low‐rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components." Magnetic Resonance in Medicine 73, no. 3 (2015): 1125-1136.
[4]. Z. P. Liang, “Spatiotemporal imaging with partially separable functions,” in 2007 IEEE 4th International Symposium on Biomedical Imaging (ISBI), 2007, pp. 988-991.
[5]. J. P. Haldar and Z.-P. Liang, “Spatiotemporal imaging with partially separable functions: A matrix recovery approach,” in 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2010, pp. 716-719.
[6]. S. G. Lingala, Y. Hu, E. DiBella, and M. Jacob, “Accelerated dynamic MRI exploiting sparsity and low-rank structure: kt SLR,” IEEE Transactions on Medical Imaging, vol. 30, no. 5, pp. 1042–1054, 2011.
[7]. R. Otazo, E. Candes, and D. K. Sodickson,“Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components,” Magnetic Resonance in Medicine, vol. 73, no. 3, pp. 1125-1136, 2015.
[8]. J. Schlemper, J. Caballero, J.V. Hajnal, A. Price, D. Rueckert, “A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction”, IEEE TMI, DOI: 10. 1109/TMI.2017.2760978 (2017)
[9]. Qin, Chen, Joseph V. Hajnal, Daniel Rueckert, Jo Schlemper, Jose Caballero, and Anthony N. Price. "Convolutional recurrent neural networks for dynamic MR image reconstruction." IEEE transactions on medical imaging (2018).
[10]. Wang S, Ke Z, Cheng H, et al. DIMENSION: Dynamic MR imaging with both k-space and spatial prior knowledge obtained via multi-supervised network training. NMR in Biomedicine. 2019;e4131. https://doi.org/10.1002/nbm.4131.
[11]. Ke, Z., Huang, W., Cheng, J., Liu, X., Zheng, H., Ying, L., ... & Liang, D. (2020). Deep Low-rank Prior in Dynamic MR Imaging. arXiv preprint arXiv:2006.12090.
[12]. Zhang, J., & Ghanem, B. (2018). ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1828-1837).
[13]. Cai, J. F., Candès, E. J., & Shen, Z. (2010). A singular value thresholding algorithm for matrix completion. SIAM Journal on optimization, 20(4), 1956-1982.
[14]. Walsh, D. O., Gmitro, A. F., & Marcellin, M. W. (2000). Adaptive reconstruction of phased array MR imagery. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 43(5), 682-690.
Figures