1945
Deep Manifold Learning for Dynamic MR Imaging1Shenzhen Institutes of Advanced Technology, Shenzhen, China, 2University at Buffalo, The State University of New York, Buffalo, NY, United States
Synopsis
Manifold learning has achieved success in cardiac MRI. It models the dynamic images as points on a smooth, low dimensional manifold in high dimensional space. The low dimensional assumption is extracted as a regularizer, but corresponding algorithms are not performed along with the manifold's nonlinear structure. In this paper, we propose a deep manifold learning for dynamic MR imaging. The manifold assumption is no longer taken as the regularization term in the proposed method, but the deep optimization model is directly developed on the nonlinear manifold. The validation on in vivo data shows that our method can achieve improved reconstruction.
Introduction
It is essential to improve the temporal and spatial resolution of cardiac MR imaging by using fast imaging method without sacrificing image quality. As an extension of compressed sensing (CS) methods [1-3], manifold learning [4-6] has made good progress in Dynamic MR imaging. These manifold learning methods assume that dynamic data are adjacent points on a smooth low-dimensional manifold. The reconstruction task is modeled as a manifold regularization problem in linear Euclidean spaces. For example, SToRM [4] relied on navigator signals to compute the manifold Laplacian matrix, and a variable splitting based algorithm was used to solve for an L1-SToRM formulation. Although these works make great contributions to dynamic MR imaging, the following issues still need to be addressed: 1) the adjacent-point hypothesis is located in nonlinear manifolds, while corresponding algorithms are not performed along with the nonlinear structure of the manifold; 2) Manifold regularization, as an extension of compressed sensing framework, cannot escape the essential iterative reconstruction process, and tedious reconstruction time and parameter selection cannot be avoided. Recently, deep learning (DL) has been introduced to speed up dynamic MR reconstruction [7-10]. For example, DIMENSION [9] developed a multi-supervised network training technique to simultaneously constrain the frequency domain information and spatial domain information. These DL-based methods unroll sparse driven optimization into neural networks in linear Euclidean spaces [10], while the manifold prior has not been used in these DL methods. Although MoDL-SToRM introduced manifold prior to DL-based methods, it still a regularization problem in Euclidean linear space. Our work tries to develop the deep optimization model on a nonlinear manifold directly.Theory and method
In this paper, we propose a deep manifold learning for dynamic MR imaging. In particular, we design a low-rank tensor manifold to characterize the strong temporal correlation of dynamic signals:$$M_r:=\{x\in C^{n_xn_yn_t}|\text{rank}(x)=r\}\ \ \ \ \ \ \ \ \ \ (1)$$
Then, the constraint optimization problem on the low-rank tensor manifold can be considered as follows:
$$\min_{x\in M_r}\ f_M=||Ax-y||_2^2\ \ \ \ \ \ \ \ \ \ (2)$$
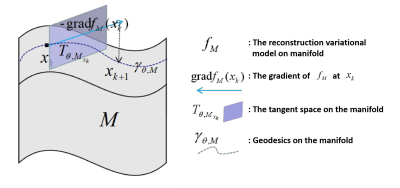
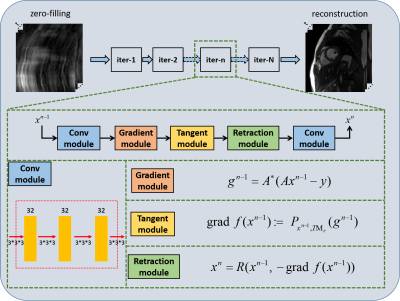
An optimization process is expanded on this manifold, as shown in Figure 1, including gradient calculation, tangent space projection, and retraction.
1). Compute the gradient of objection:
$$g_k=A^*(Ax_k-y)\ \ \ \ \ \ \ \ \ \ (3)$$
2). Project it to Tangent space:
$$\text{grad}\ f(x_k):=P_{x_k, TM_r}(g_k)\ \ \ \ \ \ \ \ \ \ (4)$$
3. Iterate by Retraction:
$$\text{grad}\ x_{k+1}=R(x_k, -\text{grad}\ f(x_k))\ \ \ \ \ \ \ \ \ \ (5)$$
The details of the projector $$$P_{x_k, TM_r}(.)$$$ and retraction operator $$$R(.)$$$ can be found in [12]. Finally, the optimization process on the manifold is unrolled to neural networks, dubbed as Manifold-Net. Manifold-Net is composed of N cascade blocks, and each block includes a convolution module, gradient module, tangent module, and retraction module. This manifold has many advantages, such as 1) Compared with the traditional manifold regularization methods, the optimization process of Manifold-Net is developed on the manifold, which accords with manifold hypothesis better; 2) Compared with the sparse driven DL methods, it explores the manifold prior and is expected to further improve the reconstruction results.
Experiment
The fully sampled cardiac cine data were collected from 30 healthy volunteers on a 3T scanner (MAGNETOM Trio, Siemens Healthcare, Erlangen, Germany) with a 20-channel receiver coil array. For each subject, 10 to 13 short-axis slices were imaged with the retrospective electrocardiogram (ECG)-gated segmented bSSFP sequence during breath-hold. The following sequence parameters were used: FOV = 330*330 mm, acquisition matrix = 256*256, slice thickness = 6 mm, and TR/TE = 3.0 ms/1.5 ms. The acquired temporal resolution was 40.0 ms and reconstructed to produce 25 phases to cover the entire cardiac cycle. The raw multi-coil data of each frame were combined by an adaptive coil combine method [13] to produce a single-coil complex-valued image. We obtained 1548 2D-t cardiac MR data for training and 45 data for testing. The models were implemented on an Ubuntu 16.04 LTS (64-bit) operating system equipped with an Intel Xeon E5-2640 Central Processing Unit (CPU) and a Tesla TITAN Xp Graphics Processing Unit (GPU, 12GB memory). The open framework Tensorflow was used.Results
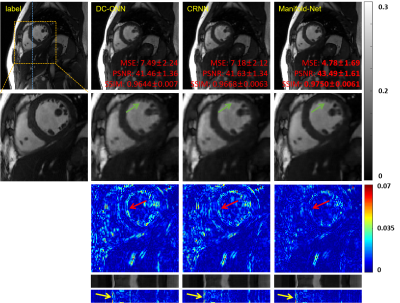
To demonstrate the proposed manifold learning method's efficacy, we compared it with two DL-based methods, namely DC-CNN [7] and CRNN [8] at 8-fold acceleration. The reconstructions of these methods are shown in Figure 3. The two DL-based reconstruction results contain less structural details and more artifacts than that of the proposed method. We also enlarge the cardiac region's error maps, which show that our approach has the best reconstruction performance on the cardiac area, especially the details marked by the green arrow. The y-t images, which are extracted from 124-th slice along the y and temporal dimensions, can also clearly illustrate the superior performance of the proposed method. We also provide quantitative evaluations (MSE, PSNR, SSIM), and Manifold-Net achieves optimal quantitative evaluations.Conclusion
In this paper, we propose a deep manifold learning for MR cardiac imaging. The comparisons with DC-CNN and CRNN show that our method can achieve improved reconstruction results. To our knowledge, this work represents the first study applying a deep manifold optimization to dynamic MR images.Acknowledgements
This work was supported in part by the National Key R&D Program of China (2020YFA0712202, 2017YFC0108802 and 2017YFC0112903); National Natural Science Foundation of China (61771463, 81830056, U1805261, 81971611, 61871373, 81729003, 81901736); Natural Science Foundation of Guangdong Province (2018A0303130132); Shenzhen Key Laboratory of Ultrasound Imaging and Therapy (ZDSYS20180206180631473); Shenzhen Peacock Plan Team Program (KQTD20180413181834876); Innovation and Technology Commission of the government of Hong Kong SAR (MRP/001/18X); Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000)References
[1]. Jung, Hong, Jong Chul Ye, and Eung Yeop Kim. "Improved k–t BLAST and k–t SENSE using FOCUSS." Physics in Medicine & Biology 52, no. 11 (2007): 3201.
[2]. Lingala, Sajan Goud, Yue Hu, Edward DiBella, and Mathews Jacob. "Accelerated dynamic MRI exploiting sparsity and low-rank structure: kt SLR." IEEE transactions on medical imaging30, no. 5 (2011): 1042-1054.
[3]. Otazo, Ricardo, Emmanuel Candès, and Daniel K. Sodickson. "Low‐rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components." Magnetic Resonance in Medicine 73, no. 3 (2015): 1125-1136.
[4]. Poddar, S., & Jacob, M. (2015). Dynamic MRI using smoothness regularization on manifolds (SToRM). IEEE transactions on medical imaging, 35(4), 1106-1115.
[5]. Nakarmi, U., Wang, Y., Lyu, J., Liang, D., & Ying, L. (2017). A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic MRI. IEEE transactions on medical imaging, 36(11), 2297-2307.
[6]. Shetty, G. N., Slavakis, K., Bose, A., Nakarmi, U., Scutari, G., & Ying, L. (2019). Bi-linear modeling of data manifolds for dynamic-MRI recovery. IEEE Transactions on Medical Imaging, 39(3), 688-702.
[7]. J. Schlemper, J. Caballero, J.V. Hajnal, A. Price, D. Rueckert, “A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction”, IEEE TMI, DOI: 10. 1109/TMI.2017.2760978 (2017)
[8]. Qin, Chen, Joseph V. Hajnal, Daniel Rueckert, Jo Schlemper, Jose Caballero, and Anthony N. Price. "Convolutional recurrent neural networks for dynamic MR image reconstruction." IEEE transactions on medical imaging (2018).
[9]. Wang S, Ke Z, Cheng H, et al. DIMENSION: Dynamic MR imaging with both k-space and spatial prior knowledge obtained via multi-supervised network training. NMR in Biomedicine. 2019;e4131. https://doi.org/10.1002/nbm.4131.
[10]. Ke, Z., Huang, W., Cheng, J., Liu, X., Zheng, H., Ying, L., ... & Liang, D. (2020). Deep Low-rank Prior in Dynamic MR Imaging. arXiv preprint arXiv:2006.12090.
[11]. Biswas, S., Aggarwal, H. K., & Jacob, M. (2019). Dynamic MRI using model‐based deep learning and SToRM priors: MoDL‐SToRM. Magnetic resonance in medicine, 82(1), 485-494.
[12]. Kressner, D., Steinlechner, M., & Vandereycken, B. (2014). Low-rank tensor completion by Riemannian optimization. BIT Numerical Mathematics, 54(2), 447-468.
[13]. Walsh, D. O., Gmitro, A. F., & Marcellin, M. W. (2000). Adaptive reconstruction of phased array MR imagery. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 43(5), 682-690.
Figures