1944
Unsupervised Dynamic Image Reconstruction using Deep Generative Adversarial Networks and Total Variation Smoothing1Stanford University, Palo Alto, CA, United States
Synopsis
Deep learning (DL)-based image reconstruction methods have achieved promising results across multiple MRI applications. However, most approaches require large-scale fully-sampled ground truth data for supervised training. Acquiring fully-sampled data is often either difficult or impossible, particularly for dynamic datasets. We present a DL framework for MRI reconstruction which does not use fully-sampled data. We test the proposed method in two scenarios: retrospectively undersampled cine and prospectively undersampled abdominal DCE. Our unsupervised method can produce faster reconstructions which are non-inferior to compressed sensing. Our novel proposed method can enable accelerated imaging and accurate reconstruction in applications where fully-sampled data is unavailable.
Introduction
Techniques based on parallel imaging (PI) 1,2 and compressed sensing (CS) 3 have successfully improved the quality of accelerated MRI scans. Deep learning (DL) methods 4–13 have recently shown to be more potentially powerful than traditional methods, providing more robustness, higher quality, and faster reconstruction speed. However, these techniques require a large number of fully-sampled acquisitions for supervised training. This poses a problem for dynamic imaging applications where the collection of fully-sampled datasets is difficult, or impossible. Specifically, for some dynamic imaging, the dynamics of the contrast are too fast to collect fully sampled data, which is a great challenge for supervised-based DL methods.In this work, we propose a framework for reconstruction of dynamic datasets without fully-sampled data. The method has been applied for reconstructing retrospectively undersampled cine datasets and for prospectively undersampled dynamic contrast enhanced (DCE) datasets.
Methods
Theory: A promising direction to address unsupervised MRI reconstruction is using generative adversarial networks (GANs) 14 due to their usefulness in creating visually appealing images 15, modeling data distributions 16,17, and constructing models for supervised MRI reconstruction 6,7,18. Recently, Bora et al. 19 proposed a framework for learning generative models from underdetermined linear systems, a problem which is similar to unsupervised MRI reconstruction. Our novel proposed objective is:$$\min_{G}\max_{D}(\mathbb{E}_{y\sim{p_y}}q(D(y^{train})) + \mathbb{E}_{y\sim{p_{y}}A\sim{p_{A}}}[
1-D(A(G(y^{input})))]) $$
where D is the discriminator, G is the generator, and A is the inverse model of the subsampled measurements. We reconstruct a set of input subsampled k-space data yinput. We use a separate training dataset as the real measurements that are fed into the discriminator, ytrain. The discriminator is trained to distinguish between real measurements and generated measurements. We use WGAN-GP, where the quality function is q(t) = t. Figure 1a illustrates an example of supervised reconstruction. Figure 1b illustrates our unsupervised MRI reconstruction framework.
Network architecture: An unrolled network 8 based on the Iterative Shrinkage-Thresholding Algorithm (ISTA) 21 is used as the generator architecture, shown in Figure 2a. The discriminator architecture, based on a simple convolutional neural network with residual structure, is shown in Figure 2b.
Datasets: Two datasets were obtained with Institutional Review Board (IRB) approval and subject informed consent. The first was a set of fully-sampled bSSFP 2D cardiac cine datasets that were acquired from 15 volunteers at different cardiac views on 1.5T and 3.0T GE scanners using 32-channel cardiac coils. All datasets were coil compressed to 8 virtual channels, split slice-by-slice and retrospectively undersampled using random variable-density sampling (R=2-5).
The second consisted of DCE acquisitions of the abdomen. 886 subjects were used for training and 50 subjects were used for testing. The raw data was compressed from 32 channels to 6 virtual channels 22. Images were prospectively subsampled with an acceleration factor of 5 using variable density Poisson-disc sampling. We used the optimal hyperparameters from the network trained on the cine dataset to train the DCE network because cine is another dynamic case which, unlike DCE, has fully-sampled ground truth.
We compared image metrics of our method against CS with a spatiotemporal total variation prior for the cine dataset and against CS with a low-rank prior for the DCE dataset.
Results
Representative cine reconstructions are shown in Figure 3. Image quality metrics comparisons are shown in Figure 4. Representative DCE reconstructions are shown in Figure 5a. Our proposed method produces reconstruction with non-inferior quality to CS. A comparison of the average DCE inference time is shown in Figure 5b. The inference time of our unsupervised method is approximately 2.98 times faster than CS.Discussion
Our unsupervised generative method allows the training of high quality image reconstruction DL models when fully-sampled data is difficult or impossible to obtain. Our unsupervised method is much faster than CS and produces reconstructions of non-inferior quality. Our method is able to estimate the underlying data distribution of fully-sampled k-space with no fully-sampled data. Data consistency and reducing the spatial and temporal TV helps sharpen the images.The main advantage of this method over existing DL reconstruction methods is the elimination of fully-sampled data. Another benefit is that other additional datasets are not needed to use as ground-truth, as in some other works on semi-supervised training 23. Additionally, the method produces non-inferior reconstructions compared to baseline CS methods while having much faster inference time than CS. The resulting reconstruction of our model is non-iterative, which is a major advantage of our method. In future work, we will experiment further with exploiting known temporal priors.
Conclusion
In this work, we propose an unsupervised GAN framework for reconstruction of dynamic datasets without using ground truth. We show that the proposed method is not inferior to existing traditional methods such as compressed sensing. In contrast to most deep learning reconstruction techniques, which are supervised, this method does not need any fully-sampled data. With the proposed method, accelerated imaging and accurate reconstruction can be performed in applications in cases where fully-sampled datasets are difficult to obtain or unavailable.Acknowledgements
Our group receives research support from GE Healthcare and NIH.References
1. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med Med. 2002;47(6):1202-1210. doi:10.1002/mrm.10171
2. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med. 1999.
3. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195. http://doi.wiley.com/10.1002/mrm.21391.
4. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018;79(6):3055-3071. doi:10.1002/mrm.26977
5. Chen F, Taviani V, Malkiel I, et al. Variable-Density Single-Shot Fast Spin-Echo MRI with Deep Learning Reconstruction by Using Variational Networks. Radiology. 2018;289(2):366-373. doi:10.1148/radiol.2018180445
6. Mardani M, Gong E, Cheng JY, et al. Deep generative adversarial neural networks for compressive sensing MRI. IEEE Trans Med Imaging. 2019. doi:10.1109/TMI.2018.2858752
7. Yang G, Yu S, Dong H, et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Trans Med Imaging. 2018;37(6):1310-1321. doi:10.1109/TMI.2017.2785879
8. Diamond S, Sitzmann V, Heide F, Wetzstein G. Unrolled Optimization with Deep Priors. http://arxiv.org/abs/1705.08041. Published May 22, 2017.
9. Cheng JY, Chen F, Alley MT, Pauly JM, Vasanawala SS. Highly Scalable Image Reconstruction using Deep Neural Networks with Bandpass Filtering. May 2018. http://arxiv.org/abs/1805.03300.
10. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging. 2019. doi:10.1109/TMI.2018.2865356
11. Souza R, Lebel RM, Frayne R, Ca R. A Hybrid, Dual Domain, Cascade of Convolutional Neural Networks for Magnetic Resonance Image Reconstruction. In: Proceedings of Machine Learning Research 102:437–446. ; 2019.
12. Eo T, Jun Y, Kim T, Jang J, Lee HJ, Hwang D. KIKI-net: Cross-domain Convolutional Neural Networks for Reconstructing Undersampled Magnetic Resonance Images. Magn Reson Med. 2018. doi:10.1002/mrm.27201
13. Cole EK, Cheng JY, Pauly JM, Vasanawala SS. Analysis of Deep Complex-Valued Convolutional Neural Networks for MRI Reconstruction. arXiv:200401738. April 2020. http://arxiv.org/abs/2004.01738.
14. Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Networks. Adv Neural Inf Process Syst. 2014:2672-2680. doi:10.1001/jamainternmed.2016.8245
15. Zhu J, Krähenbühl P, Shechtman E, Efros A. Generative Visual Manipulation on the Natural. Eur Conf Comput Vis. 2016. doi:10.1007/978-3-319-46454-1
16. Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. In: Advances in Neural Information Processing Systems. ; 2014. doi:10.3156/jsoft.29.5_177_2
17. Radford A, Metz L, Chintala S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. In: 4th International Conference on Learning Representations, ICLR 2016 - Conference Track Proceedings. ; 2016.
18. Mardani M, Gong E, Cheng JY, et al. Deep Generative Adversarial Networks for Compressed Sensing Automates MRI. http://arxiv.org/abs/1706.00051. Published May 31, 2017.
19. Bora A, Price E, Dimakis AG. Ambientgan: Generative models from lossy measurements. In: 6th International Conference on Learning Representations, ICLR 2018 - Conference Track Proceedings. ; 2018.
20. Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Phys D Nonlinear Phenom. 1992. doi:10.1016/0167-2789(92)90242-F
21. Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J Imaging Sci. 2009;2(1):183-202. doi:10.1137/080716542
22. Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn Reson Med. 2013. doi:10.1002/mrm.24267
23. Lei K, Mardani M, Pauly JM, Vasawanala SS. Wasserstein GANs for MR Imaging: from Paired to Unpaired Training. http://arxiv.org/abs/1910.07048. Published October 15, 2019.
Figures
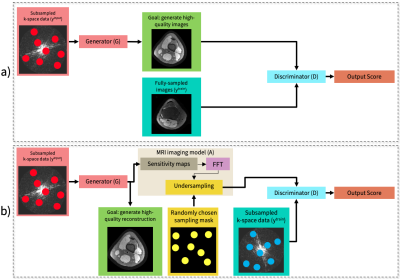
Figure 1. (a) Framework overview example in a supervised setting with a conditional GAN when fully-sampled datasets are available.
(b) Our proposed framework overview in an unsupervised setting. A sensing matrix comprised of coil sensitivity maps, an FFT and a randomized undersampling mask is applied to the generated image to simulate the imaging process. The discriminator takes simulated and observed measurements as inputs and tries to differentiate between them. The generator’s loss is based on the discriminator as well as reducing spatial and temporal variation.
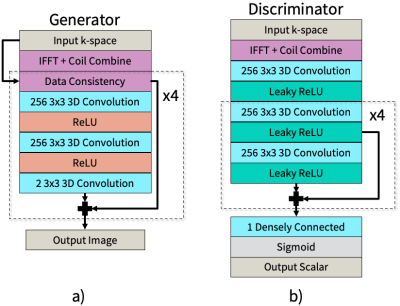
Figure 2. Network architectures. All convolutional layers are 3D, which operate on 2D plus time volumes.
(a) The generator architecture, which is an unrolled network based on the Iterative Shrinkage-Thresholding Algorithm and includes data consistency. The generator is trained in both k-space and image domain.
(b) The discriminator architecture, which uses leaky ReLU in order to backpropagate small negative gradients into the generator. The discriminator is trained only in image domain.
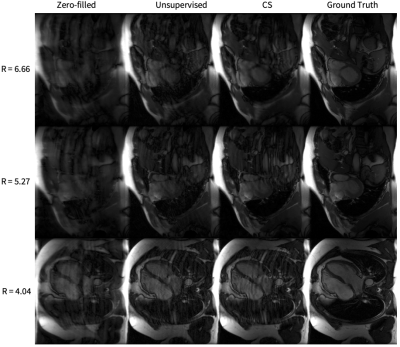

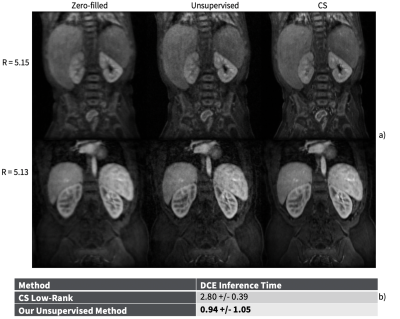
Figure 5. (a) Representative DCE images. The leftmost column is the input zero-filled reconstruction, the middle column is our generator’s reconstruction, and the rightmost column is the CS reconstruction. The generator improves the input image quality by recovering sharpness and adding more structure to the input images.
(b) Comparison of DCE inference time per three-dimensional DCE volume (2D + time) between CS low-rank and our unsupervised GAN. Our method is approximately 2.98 times faster.