1910
Microvascular MRI Signal Changes in the Presence of Amyloid-Beta Plaques or Microbleeds: A Simulation Study1Radiology, Kyung Hee University Hospital at Gangdong, Seoul, Korea, Republic of, 2Medicine, Kyung Hee University, Seoul, Korea, Republic of, 3Physics, Kyung Hee University, Seoul, Korea, Republic of, 4Biomedical Engineering, Ulsan National Institute of Science and Technology, Ulsan, Korea, Republic of
Synopsis
We simulated the changes in microvascular (MV) MRI signals with and without existing amyloid-beta plaques or microbleeds in an imaging voxel. The Monte Carlo simulations with the finite perturber method were used to calculate MV indices of mean vessel diameter (mVD), vessel size index (VSI), mean vessel density (Q), blood volume fraction (BVf), and microvessel-weighted imaging (MvWI). The simulation was performed with three different voxel environmental conditions: only the MV structures, MV structures with amyloid-beta plaques, and MV structures with microbleeds.
Introduction
Alzheimer’s disease (AD) is the most common age-related neurodegenerative disorder, and leads to cognitive decline and memory loss. AD is a complex and progressive disease that is caused by an abnormal accumulation of amyloid-beta (Aβ)42 plaque and tau proteins. Furthermore, cerebral microbleeds, which are hemosiderin deposits in the brain, occur more frequently in patients with AD than in the general population. Both microbleeds and Aβ42, which comprise metallic materials, have a higher susceptibility than the surrounding tissue in developing local field inhomogeneities. Therefore, both microbleeds and Aβ42 should be considered while evaluating microvascular (MV) structure changes in the AD brain.Purpose
There is currently no study in the literature that has evaluated MV alterations with accumulation of amyloid-beta plaque proteins or the presence of microbleeds in the AD brain. Therefore, in this study, we simulated MRI signal changes by assuming three different environmental conditions in the imaging voxel: only the normal MV structures, normal MV structures in the presence of amyloid-beta plaques, and normal MV structures in the presence of microbleeds. Alterations in MV imaging indices such as mean vessel diameter, vessel size index, mean vessel density, blood volume fraction, and microvessel-weighted imaging were calculated by using the differences in relaxation rates, ΔR2* and ΔR2, through Monte Carlo simulations with application of FPM for the three conditions.Theory
1. Modeling of vascular structures with and without amyloid-beta plaques or microbleedsa) Modeling of vascular structures:
With a 3-dimensional (3D) binary voxel of 256 x 256 x 256 mm3 (cell size = 1 mm3), we assumed that vascular structures were randomly distributed in the voxel with the blood volume fraction of the vessels equal to 2% and that the vessels were finite cylinders. The radius of each cylinder ranged from 1 to 30 while holding the fractional volume constant at 2%. Figure 1 shows a 3D image of the modeled vascular structures (1a) and the corresponding cross-section taken along the z-axis (1b) of Figure 1a.
b) Modeling of vascular structures with amyloid-beta plaques or microbleeds:
Within the 3D binary voxel of the vascular structures, we modeled the amyloid-beta plaques and microbleeds as spheres. The average Aβ loads have been reported as 3.81% (± 2.47) for AD patients and 1.83% (±1.84) for non-demented subjects (1,2). The radius was set at between 1~20 to model the amyloid-beta plaque within the voxel (3) and between 1~100 to model the microbleed within the voxel (4). Figure 1c shows a 3D image of the modeled vascular structures with the amyloid-beta plaque or microbleed structures, and Figure 1d shows the corresponding cross-section taken along the z-axis of Figure 1c.
2. Calculation of MRI signals and relaxation rates
The finite perturbation method (FPM) method was used to calculate the change in a magnetic field due to susceptibility differences between the vessels and the spherical structures (5). The magnetic field differences between intra- and extra-vascular spaces and between the inner and outer spheres were calculated using the following equation at three different main magnetic field strengths ( ), which were 1.5 T, 3 T, and 7 T.
3. Calculation of the microvascular indices
The following MV indices were calculated using the simulation results of the differences in the transverse relaxation rates, ΔR2* and ΔR2: mean vessel diameter (mVD) (6), vessel size index (VSI) (7), mean vessel density (Q), blood volume fraction (BVf), and microvessel-weighted imaging (MvWI) (8).
Methods
The simulations were repeated with three different main magnetic field strengths (1.5 T, 3 T, and 7 T) and two different contrast agents, Gadolinium (Gd)–chelated and Superparamagnetic Iron Oxide Nanoparticles (SPION) in three different voxel environmental conditions of only the MV structures, MV structures with amyloid-beta plaques, and MV structures with microbleeds. This simulation was performed using a Matlab script on a personal computer, which had an AMD Ryzen 1700 processor with 32GB memory. Table 1 summarizes the parameters used in the simulation.Results
Figure 2 shows the simulation results for the variations in MV indices against amyloid plaque loads for microvessel size set at 5 μm at gradient-echo time of 40 ms and spin-echo time of 80 ms. mVD decreased with increasing plaque loads. mVD was similar at 3 T and 7 T, and with either Gd or SPION. In the amyloid-plaque model, mVD and VSI decreased with increasing plaque loads, but BVf, Q, and MvWI increased with increasing plaque loads. In the microbleed model, the MV indices of mVD and VSI increased with increasing vessel size. The MV indices of mVD, BVF, VSI and MvWI increased with increasing microbleed loads, but Q did not.Conclusion
In conclusion, all MV indices were sensitive enough to map accumulations of amyloid plaques, but did not vary with increasing vessel size. The MV indices, except Q, were sensitive to changes in microbleed loads and microvessel size. Therefore, we recommend evaluating MV structure changes in the AD human brain using 3T MRI with a Gadolinium (Gd) contrast agent.Acknowledgements
This study was supported by the Basic Science Research Program through the National Research Foundation (NRF) of Korea funded by the Ministry of Education (2016R1D1A1B03930720, GHJ) and the National Research Foundation of Korea (NRF) grant funded by Ministry of Science and ICT (No. 2020R1A2C1004749, GHJ), Republic of Korea.References
1) Bennett, D. A., et al. Archives of neurology 61, 378-384 (2004).
2) Martikainen, P. et al. Neuropathology and applied neurobiology 36, 41-54 (2010).
3) Galea, E. et al. PNAS 112, 15556-15561 (2015).
4) Reuter, B. et al. Frontiers in aging neuroscience 8, 170 (2016).
5) Pathak, A. P., et al. NeuroImage 40, 1130-1143 (2008).
6) Dennie, J. et al. Magnetic resonance in medicine 40, 793-799 (1998).
7) Tropres, I. et al. Magnetic resonance in medicine 45, 397-408 (2001).
8) Jung, H. S. et al. NMR in biomedicine 29, 690-701 (2016).
Figures
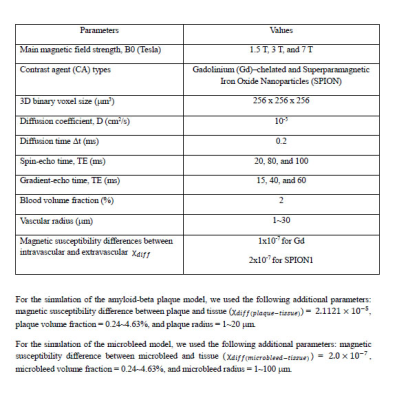
Figure 1. Simulation modeling
This figure shows the simulation models with 3D image of the modeled vascular structure (1a) and the corresponding cross-section taken along the z-axis (1b), 3D image of the modeled Aβ or microbleeds (1c) and the corresponding cross-section taken along the z-axis (1d), and 3D image of the modeled vascular structure with the amyloid-beta plaque or microbleed structure (1e) and the corresponding cross-section taken along the z-axis (1f).
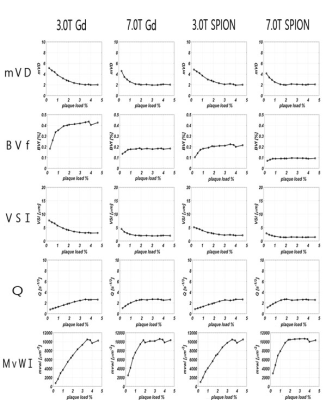
Figure 2. Simulation results of microvascular indices with amyloid plaque model.
This figure shows the changes of the microvascular indices with a vessel size of 5 μm with different amyloid loads at the same echo times in the amyloid plaque model.
mVD, mean vessel diameter; BVF, blood volume fraction; VSI, vessel size index; Q, mean vessel density; MvWI, microvessel-weighted imaging