1842

Simultaneous Quantification of Mean Intracellular Water Lifetime and Cell Size Using Temporal Diffusion Spectroscopy

xiaoyu jiang¹, sean p devan¹, john c. gore¹, and junzhong xu¹
¹Vanderbilt University Institute of Imaging Science, nashville, TN, United States

Synopsis

There is an increasing interest in characterizing tissue microstructure using multi-compartment diffusion MRI models involving multiple b values and diffusion times ($$$t_{diff}$$$s). However, previous models usually ignore water exchange between intra- and extracellular compartments, which limits the accuracy of the fitted model parameters and potentially their interpretation as indicators of disease progression or treatment response. Here, we propose a simplified biophysical model of solid tissues that allows derivation of the mean intracellular water lifetime ($$$\tau_{i}$$$) and other microstructural parameters (e.g., cell size d) simultaneously from the $$$t_{diff}$$$ dependence of diffusion MRI signals.

Introduction

Transcytolemmal water exchange plays a fundamental role in cell physiology (1). The intracellular water lifetime, $$$\tau_{i}$$$, is a key biophysical parameter that describes transcytolemmal water exchange and which has been suggested as an indicator of disease progression and treatment response (2). In vivo measurements of $$$\tau_{i}$$$ are usually achieved using paramagnetic contrast agent methods (3,4), while diffusion-based methods such as the constant-gradient (5) and FEXI (filtered exchange imaging) (6) are either limited by SNR or influenced by other confounding effects. We propose a simplified model that incorporates transcytolemmal water exchange in a multi-compartment diffusion-based IMPULSED method (7-9) that has been developed previously to extract microstructural parameters (e.g., mean cell size d, and intracellular volume fraction v_in assuming no water exchange. Using simulations, we show that not only can the proposed method estimate $$$\tau_{i}$$$ and d accurately, but also it reduces the underestimation of IMPULSED-derived v_in.

Theory

The influence of cell membrane permeability (a function of and ) on MR diffusion measurements depends on $$$t_{diff}$$$ (10): it is negligible when $$$t_{diff}$$$ is relatively short while it impacts diffusion signals significantly when t_{diff} is relatively long. Therefore, a combination of acquisitions of both oscillating gradients as in OGSE (oscillating gradient spin echo) for short $$$t_{diff}$$$ (e.g., ≤ 5 ms) and bipolar gradients as in PGSE (pulsed gradient spin echo) or STEAM (stimulated echo acquisition mode) for relatively long $$$t_{diff}$$$ (e.g., ≥30 ms) provides sufficient coverage for practical characterizations of $$$\tau_{i}$$$ and d. Solid tissues are modeled as two-compartments in which water diffuses and exchanges. Cells are approximated as permeable spheres with mean diameter d, intracellular diffusion coefficient D_in (fixed to 1.56 µm²/ms as suggested in (9)), and intracellular water lifetime $$$\tau_{i}$$$. The analytic expressions describing hindered/restricted diffusion in extra/intra-cellullar spaces are the same as in the previous IMPULSED method, but the effect of water diffusion is incorporated differently in different $$$t_{diff}$$$ ranges: 1. For short $$$t_{diff}$$$ (e.g., 5 ms using 50 Hz of OGSE), the water exchange is ignored and the signal model is the same as the IMPULSED analysis (7).
2. For long $$$t_{diff}$$$ (e.g., ≥ 30 ms), we adapted the modified $$$K\ddot{a}rger$$$ model (11) that includes both restricted diffusion and exchange between pools. This model assumes short gradient pulses (i.e., δ ≪ Δ) so that diffusion is considered only during two short gradient pulses, while relaxation and exchange effects occur throughout the pulse sequence. Using this hybrid model, we are able to extract d, v_in and $$$\tau_{i}$$$ from diffusion signals acquired with different $$$t_{diff}$$$.

Methods

Finite difference simulations (12) were performed on modeled tissues consisting of closely packed spherical cells with v_in = 61.8%, D_ex = 1 µm²/ms, and D_in = 1.56 µm²/ms, d from 10 to 20 µm with each incorporated 15 different $$$\tau_{i}$$$’s: 50, 60, 70, 80, 90, 100, 125, 150, 200, 250, 300, 350, 400, 450, 500, and $$$\infty$$$ ms. Bipolar gradients with $$$t_{diff}$$$ = 30, 70, 100, 200 ms and oscillating gradients with 50 Hz ($$$t_{diff}$$$ = 5 ms) were used to generate diffusion MRI signals with a gradient rise time 0.9 ms as in clinics (9).

Results

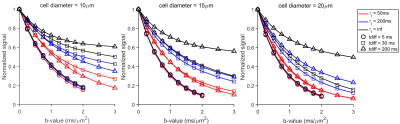
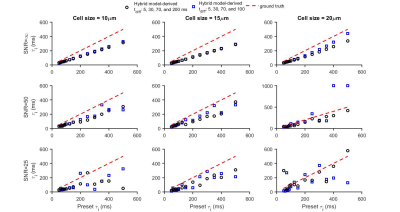
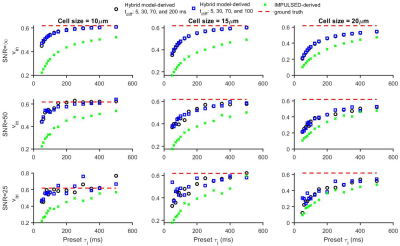
Figure 1 shows that the simulated 50 Hz OGSE signals for different cell sizes (10, 15, and 20 µm) and $$$\tau_{i}$$$s are almost the same, confirming the negligible influences of $$$\tau_{i}$$$ when $$$t_{diff}$$$ is short. By contrast, fast water exchange ( $$$\tau_{i}$$$ =50 ms) significantly affects diffusion data acquired with relatively long diffusion times. The hybrid model-derived $$$\tau_{i}$$$ and cell membrane permeability P_m (a function of $$$\tau_{i}$$$, d, and D_in (12)) show good agreement with the preset values (Figure 2&3). The noise level has a larger impact on the accuracy of the fitted $$$\tau_{i}$$$s than the fitted cell sizes (Figure 4), and this impact reduces with decreasing cell size. Expanding the range of diffusion times from 100 to 200 ms increases the sensitivity for detecting slower water exchange for larger cells. Figure 4 shows that the IMPULSED method overestimates cell sizes when fast water exchange exists, and the hybrid model improves cell size estimates. As shown in Figure 5, ignoring water exchange leads to an underestimation of intracellular volume fraction (v_in). The hybrid model corrects the bias when water exchange is relatively slow (e.g., $$$\tau_{i}$$$ >200 ms).

Discussion and Conclusion

We propose a simple biophysical model to provide simultaneous assessment of intracellular water lifetime $$$\tau_{i}$$$ and cell size d in physiologically relevant ranges using diffusion MRI with clinically achievable diffusion times (5-100 ms). Because of the involvement of the modified $$$K\ddot{a}rger$$$ model for long $$$t_{diff}$$$ data, it is challenging for this model to quantify fast water exchange ($$$\tau_{i}\gg\frac{cell\:radius^2 }{intrinsic intracellular diffusion coefficient (D)}$$$), e.g., $$$\tau_{i}$$$ < 10 ms and 35 ms for cells with diameters of 10 and 20 µm, respectively, assuming D is ~ 3 µm²/ms (free water diffusion rate at body temperature). Moreover, the assumption of short gradient pulses may not be valid for cases that use long pulse durations. Efforts to develop a general approach that models diffusion and water exchange under finite durations of gradients are ongoing.

Acknowledgements

No acknowledgement found.

References

1. Amiry-Moghaddam M, Ottersen OP. The molecular basis of water transport in the brain. Nature reviews Neuroscience 2003;4(12):991-1001.

2. Ruggiero MR, Baroni S, Pezzana S, Ferrante G, Geninatti Crich S, Aime S. Evidence for the Role of Intracellular Water Lifetime as a Tumour Biomarker Obtained by In Vivo Field-Cycling Relaxometry. Angewandte Chemie 2018;57(25):7468-7472.

3. Buckley DL, Kershaw LE, Stanisz GJ. Cellular-interstitial water exchange and its effect on the determination of contrast agent concentration in vivo: dynamic contrast-enhanced MRI of human internal obturator muscle. Magnetic resonance in medicine 2008;60(5):1011-1019.

4. Zhang J, Kim S. Uncertainty in MR tracer kinetic parameters and water exchange rates estimated from T1-weighted dynamic contrast enhanced MRI. Magnetic resonance in medicine 2014;72(2):534-545. 5. Meier C, Dreher W, Leibfritz D. Diffusion in compartmental systems. II. Diffusion-weighted measurements of rat brain tissue in vivo and postmortem at very large b-values. Magnetic resonance in medicine 2003;50(3):510-514.

6. Lasic S, Nilsson M, Latt J, Stahlberg F, Topgaard D. Apparent exchange rate mapping with diffusion MRI. Magnetic resonance in medicine 2011;66(2):356-365.

7. Jiang X, Li H, Xie J, Zhao P, Gore JC, Xu J. Quantification of cell size using temporal diffusion spectroscopy. Magnetic resonance in medicine 2016;75(3):1076-1085.

8. Jiang X, Li H, Xie J, McKinley ET, Zhao P, Gore JC, Xu J. In vivo imaging of cancer cell size and cellularity using temporal diffusion spectroscopy. Magnetic resonance in medicine 2017;78(1):156-164. 9. Xu J, Jiang X, Li H, Arlinghaus LR, McKinley ET, Devan SP, Hardy BM, Xie J, Kang H, Chakravarthy AB, Gore JC. Magnetic resonance imaging of mean cell size in human breast tumors. Magnetic resonance in medicine 2020;83(6):2002-2014.

10. Li H, Jiang X, Xie J, McIntyre JO, Gore JC, Xu J. Time-Dependent Influence of Cell Membrane Permeability on MR Diffusion Measurements. Magnetic resonance in medicine 2016;75(5):1927-1934. 11. Stanisz GJ, Li JG, Wright GA, Henkelman RM. Water dynamics in human blood via combined measurements of T2 relaxation and diffusion in the presence of gadolinium. Magnetic resonance in medicine 1998;39(2):223-233.

12. Li H, Jiang X, Xie J, Gore JC, Xu J. Impact of transcytolemmal water exchange on estimates of tissue microstructural properties derived from diffusion MRI. Magnetic resonance in medicine 2017;77(6):2239-2249.

Figures

Simulated diffusion signals with diffusion times = 5, 30, and 200 ms for three cell diameters (10, 15, and 20 µm) and intracellular water lifetime $$$\tau_{i}$$$s (50, 200, and $$$\infty$$$ ms).

The hybrid model-derived intracellular water lifetimes from the simulated diffusion data with three SNR levels ($$$\infty$$$, 50, and 25) and two different imaging protocols, including $$$t_{diff}$$$ = 5, 30, 70, and 100 ms (blue circles) and $$$t_{diff}$$$ = 5, 30, 70, and 200 ms (black circles).

The calculated cell membrane permeability P_m = $$$\frac{1}{\frac{6\tau_{i}}{d}-\frac{d}{10D_{in}}}$$$( $$$\tau_{i}$$$ and d are derived by hybrid model fittings, and D_in is set to be 1.56 µm²/ms since it has minor effects on the fitting of other parameters) from the simulated diffusion data with three SNR levels ($$$\infty$$$, 50, and 25) and three different cell sizes (10, 15, and 20 µm).

IMPULSED- and hybrid model-derived cell sizes from the simulated diffusion data with three SNR levels ( $$$\infty$$$, 50, and 25). The hybrid model was applied to data with two different imaging protocols, including $$$t_{diff}$$$ = 5, 30, 70, and 100 ms (blue circles) and $$$t_{diff}$$$ = 5, 30, 70, and 200 ms (black circles). The IMPULSED model was applied to data with $$$t_{diff}$$$ = 5, 30, 70, and 100 ms (green circles).

The hybrid/IMPULSED model-derived intracellular volume fractions from the simulated diffusion data with three SNR levels ($$$\infty$$$, 50, and 25). The hybrid model was applied to data with two different imaging protocols, including $$$t_{diff}$$$ = 5, 30, 70, and 100 ms (blue circles) and $$$t_{diff}$$$ = 5, 30, 70, and 200 ms (black circles). The IMPULSED model was applied to data with $$$t_{diff}$$$ = 5, 30, 70, and 100 ms (green circles).

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1842