Introduction

Magnetic resonance (MR) susceptometry provides rapid quantification of venous oxygen saturation (SvO₂) (1,2), a key physiological parameter. The magnetic susceptibility difference (Δχ) between blood and tissue varies linearly with SvO₂ and hematocrit (Hct) (3),

$$∆χ=Hct∙∆χ_0∙(1-SvO_2)\hspace{2.54cm}(1)$$

Δχ₀ is the susceptibility difference between fully deoxygenated and fully oxygenated erythrocytes. Experimentally, Δχ is determined from the local field shift (ΔB) between blood, containing paramagnetic deoxyhemoglobin within erythrocytes, and the surrounding diamagnetic tissue. For a large vein tilted by angle θ to the main field (B₀),

$$∆B=\frac{2π}{3} B_0 ∆χ∙(3cos^2 θ-1)\hspace{2.54cm}(2)$$

ΔB is obtained from a multi-echo gradient-recalled echo (mGRE) pulse sequence by computing the phase difference (Δφ_map) between two echoes separated by ΔTE,

$$∆φ_{map}=γ∆B∆TE\hspace{2.54cm}(3)$$

The proton gyromagnetic ratio is γ. SvO₂ is derived, where Δφ is measured in Δφ_map as the absolute difference between averages of intravascular phase and that of surrounding tissue (Δφ = |Δφ_vessel - Δφ_tissue|).

$$SvO_2=\left[1-\frac{2∆φ/∆TE}{γ∆χ_{do} Hct∙B_0 (cos^2 θ-\frac{1}{3})}\right]×100\hspace{2.54cm}(4)$$

The superior sagittal sinus (SSS) is ideal for quantifying SvO₂ in the brain, but static field inhomogeneity needs to be removed before extracting Δφ. An efficient and rapid approach to retrospective correction is to perform a weighted least-squares fit of the magnetic field distribution within the brain parenchyma to a second-order polynomial, with interpolation to estimate the inhomogeneity across a vessel, since field inhomogeneity is characterized by a low spatial frequency across the field-of-view (FOV) (4). The primary limitations are that precision is limited by the signal-to-noise ratio (SNR) of the brain tissue signal instead of blood and defining a region-of-interest (ROI) used to measure Δφ_tissue is subjective.
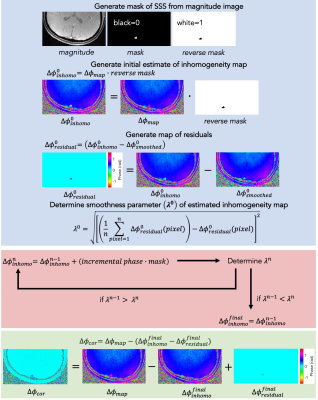
Ideally, background-field correction would leave zero average Δφ_tissue because it serves as a reference. We propose a method for removal of background field inhomogeneity that accomplishes this, based on two assumptions: (1) the static field varies smoothly over the FOV; (2) perfect field homogeneity results in zero average Δφ_tissue in regions like those surrounding the SSS. Estimation of the background field inhomogeneity contribution to intravascular phase (Δφ_inhomo) requires that assumption (1) be satisfied across the vessel ROI, while assumption (2) implies that the tissue field in Δφ_map is due only to background field inhomogeneity. A corrected map is generated by subtraction (Δφ_cor = Δφ_map - Δφ_inhomo).

Methods

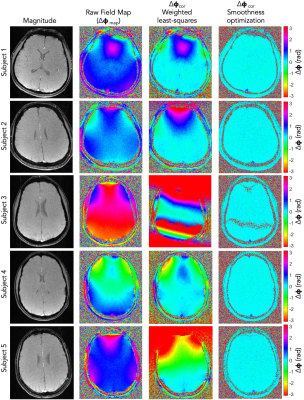
Field maps were acquired from five healthy volunteers using data from a dual-band OxFlow experiment (5) at 3 T. Two sets of Δφ_cor were generated: one by weighted least-squares fit as described by Langham et al. (4), and another by the smoothness-optimization for estimation of background field inhomogeneity, described here. The algorithm was implemented in MATLAB (The MathWorks, Inc., Natick, MA, USA) and outlined in Figure 1. A binary pixel mask is generated for the SSS. An initial estimate of the background field inhomogeneity map ($$$Δφ_{inhomo}^0$$$) is set to Δφ_map, with masked pixels zeroed. The initial $$$Δφ_{inhomo}^0$$$ is smoothed using a Wiener filter ($$$Δφ_{smoothed}^0$$$), and a convergence metric (λ⁰) computed as the root-mean-square deviation (rmsd) of the pixelwise differences between $$$Δφ_{inhomo}^0$$$ and $$$Δφ_{smoothed}^0$$$, yielding a residual phase map ($$$Δφ_{residual}^0$$$). An incremental phase offset is iteratively added to masked pixels in $$$Δφ_{inhomo}^0$$$, yielding an intermediate map ($$$Δφ_{inhomo}^n$$$, n corresponding to iteration number), the Wiener filter reapplied ($$$Δφ_{smoothed}^n$$$), and λⁿ of $$$Δφ_{residual}^n$$$ recalculated, until minimized. The residual phase distribution from the final subtraction ($$$Δφ_{residual}^{final}$$$ = $$$Δφ_{inhomo}^{final}$$$ - $$$Δφ_{smoothed}^{final}$$$) is not due to background field inhomogeneity, but the source requires further investigation. The corrected map is calculated as Δφ_cor = Δφ_map – ($$$Δφ_{inhomo}^{final}$$$ - $$$Δφ_{residual}^{final}$$$). It was empirically determined that subtraction of the final residual map results in optimal λ^final.

Results

Figure 2 shows a comparison between field maps corrected by each method. SvO₂ was computed for each case and reported as the mean ± one standard deviation for six repetitions from one scan. The SvO₂ for subject 1 was comparable between the two methods (67 ± 2% vs. 66 ± 1%). The SvO₂ for subject 2 was non-physiological when correction was done by weighted least-squares fit (88 ± 2%) but within normal range when done by smoothness-optimization (70 ± 2%). The field map for subject 3 exhibited phase-wrapping, so weighted least-squares fit failed, but smoothness-optimization led to a reasonable value (66 ± 1%). The agreement was excellent for subject 4 (67 ± 1% vs. 67 ± 1%). Subject 5 also had a non-physiological measurement by weighted least-squares fit correction (85 ± 1%) but a reasonable value by the new method (74 ± 2%).

Discussion and Conclusion

SvO₂ measurement by susceptometry-based oximetry provides high temporal resolution but requires correction for background field inhomogeneity. The weighted least-squares fit (4) requires measurement of Δφ_tissue, adding subjectivity and limiting measurement precision. The smoothness-optimization uses an objective parameter λ to determine goodness-of-fit, and does not require measurement of Δφ_tissue, theoretically enhancing precision since lumen SNR is higher. Results demonstrate reasonable agreement in SvO₂ measured by the two methods for two data sets, and a significant improvement for the other three when using the new method. Future work will focus on validating the new method on a susceptibility phantom, as well as on a larger subject cohort. Robustness of the new method to severe inhomogeneity prevalent at longer ΔTE and higher B₀ will also be evaluated.

Acknowledgements

This work is supported by the National Institutes of Health (NIH) under award number T32EB020087.