1830

Balanced SSFP Parameter Estimation by Fitting Multi-TR Ellipses

Nicholas McKibben¹, Michael Mendoza², Neal K Bangerter², and Michael N Hoff³
¹University of Utah, Salt Lake City, UT, United States, ²Department of Bioenginnering, Imperial College London, London, United Kingdom, ³Deptartment of Radiology, University of Washington, Seattle, WA, United States

Synopsis

Multiple linearly phase-cycled, multiple-TR bSSFP can be used to effectively estimate off-resonance and condition input to the PLANET algorithm to make it robust to noise and lack of available phase-cycled images. We provide methods of estimating off-resonance given 6 or 8 phase-cycles distributed across multiple-TR acquisitions. Using the elliptical signal model, it is shown that similar ellipse shape at high flip angles allow rotated ellipses to be superimposed, leading to the construction of "virtual" ellipses. Virtual ellipses are shown to be robust to noise and perform well in simulation and phantom studies.

Introduction

Balanced SSFP (bSSFP) is a fast, SNR-efficient pulse sequence with unique contrast that suffers from dark banding artifacts due to its off-resonance dependence¹. Multiple linearly phase-cycled acquisitions (phase-cycles) can be used to mitigate artifacts at the cost of scan and processing time^2,3. The bSSFP elliptical signal model describes how phase-cycled pixels trace ellipses in the complex plane^3,4 - many algorithms exploit this model to extract information beyond magnitude/phase images^5,6,7. The PLANET algorithm simultaneously estimates T1,T2 and off-resonance parameter maps⁵. However, it is not robust using fewer than ~8 phase-cycles, and at low SNR and high flip angles. PLANET field maps also suffer from phase wrapping and numerical imprecision due multiple least-squares fitting steps.

We present methods of combining phase-cycles from multiple-TR acquisitions to improve PLANET’s robustness to noise while independently estimating field maps using 6 or 8 phase-cycles.

Theory

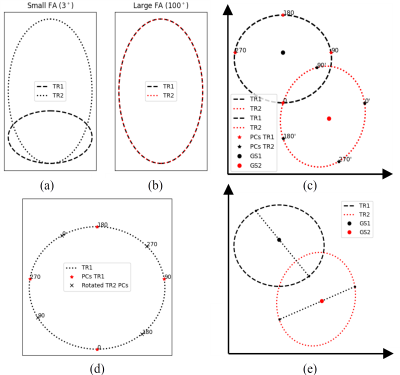
While ellipse shape generally varies with tissue and imaging parameters, high flip angles (>70°) produce approximately identically-shaped ellipses over achievable TR and tissue parameter values (Figure 1ab)⁸. Varied TR induces ellipse rotation about the origin due to accumulated off-resonant phase. (Figure 1c). Figure 1d shows that the balancing effect of the matched gradients in bSSFP also results in the phase-cycled value “traveling” around the ellipse to different relative positions as each nearly-identical “TR-ellipse” rotates about the origin.

If $$$\geq$$$4 phase-cycles are acquired on a single TR-ellipse, any static point within the ellipse can give both the demodulated band-free pixel³ and an off-resonance-like map^10,11. Setting phase-cycles to 180°-incremented phase-cycled pairs (e.g., 0°/180° or 90°/270°) allows calculation of a static geometric cross-point for each TR-ellipse. One TR-ellipse may be rotated by the angle between two elliptical geometric cross-points to create a virtual, superimposed ellipse with $$$\geq$$$8 phase-cycles due to unique phase-cycle positions. PLANET may then be used to produce parameter maps.

Since the geometric cross-point lies on a line connecting two pixels in the complex plane, the phase-cycle requirement may be reduced to 2 phase cycles on one of the ellipses (Figure 1e). Rotating this line about the origin until it intersects the geometric cross-point of the other ellipse will produce the desired off-resonance estimate.

Methods

Computer simulations on the Shepp-Logan model⁹ were generated with TR1/TR2=3ms/3.45ms, FA=100°, resolution=512x512, off-resonance varying linearly along the x-axis from [-1/TR1, 1/TR1]Hz, and additive bivariate Gaussian noise.

Doped-water phantoms were scanned on a Siemens 3T Trio scanner. All scans used FA=70°, averages=8, resolution=128x128, FOV=150x150mm2, and bandwidth=558Hz/px. A mild field perturbation was added along the x-axis to exaggerate banding artifacts. 8 linearly spaced phase-cycles on [0, 2$$$\pi$$$] at both TR=6ms and TR=12ms were acquired. SNR is reported as $$$\frac{P_{\text{signal}}}{P_{\text{noise}}}$$$.

Single-TR and multiple-TR virtual ellipse PLANET T1, T2, and field mapping algorithms were employed to process simulation and phantom data. Simulations leveraged ground truth for error and were conducted over a range of SNR values.

All methods and utilities were implemented in Python and are available in the open source ssfp package: https://pypi.org/project/ssfp/

Results

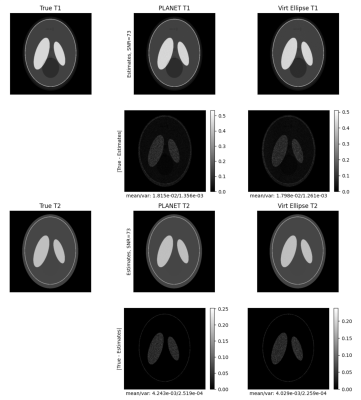
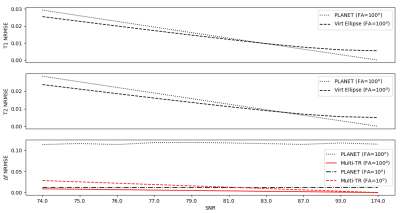
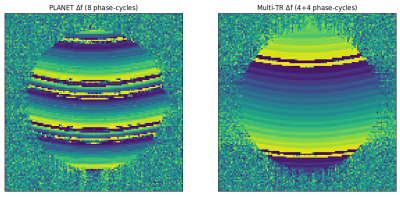
Figure 2 compares simulation results from the standard T1/T2 PLANET and the proposed virtual ellipse method. Below SNR~60 PLANET generates erroneous parameter maps at high flip angles, while methods performed similarly at SNR~70 for both T1 and T2 estimates. Figure 3 shows representative off-resonance field maps for both 8 and 6 phase-cycles. Standard PLANET yielded visible streaking artifacts and wholly unusable maps respectively, while the virtual ellipse method produced accurate maps. Figure 4 shows that at high SNR, the standard PLANET algorithm yielded more accurate T1/T2 mapping, but the virtual ellipse method performed better below SNR~85. PLANET’s off-resonance outperforms the virtual ellipse estimate at low FA and SNR values, but the virtual ellipse method outperforms when the high FA assumption holds. Figure 5 shows phantom experiment results, with PLANET suffering from noise and phase-wrapping while the virtual ellipse method producing a smoothly varying field map.

Discussion

The virtual ellipse method is more accurate than standard PLANET at high flip angles, and produces less error in noisy images given fewer phase-cycles. PLANET is susceptible to phase wrapping, leading to potentially complex post-processing steps. The proposed virtual ellipse method employs small TR and subsequent phase differences, which negates the need for phase unwrapping and permits removal of static background phase effects^10,11. PLANET also requires two cascaded least-squares fitting steps to generate field maps, while the proposed method only requires simple geometry to yield improved field maps robust to parametric variations, even when only 6 phase cycles are used. However, when off-resonance is near 0 or TR differences rotate the ellipse completely about the origin, virtual ellipse phase-cycles are no longer unique, potentially precluding PLANET T1/T2 mapping. This may be remedied by adding a phase offset to phase-cycles on one of the TR-ellipses. More analysis is required to characterize the performance of the virtual ellipse method across various TR, FA, and off-resonance values.

The proposed multiple-TR virtual ellipse methods improved upon PLANET T1/T2 mapping in medium-SNR conditions and produced high quality field maps even when only 6 phase-cycles were used.

Acknowledgements

No acknowledgement found.

References

1. Carr, H. Y. "Steady-state free precession in nuclear magnetic resonance." Physical Review 112.5 (1958): 1693.

2. Bangerter, Neal K., et al. "Analysis of multiple‐acquisition SSFP." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 51.5 (2004): 1038-1047.

3. Xiang, Qing‐San, and Michael N. Hoff. "Banding artifact removal for bSSFP imaging with an elliptical signal model." Magnetic resonance in medicine 71.3 (2014): 927-933.

4. Dharmakumar, Rohan, and Graham A. Wright. "Understanding steady‐state free precession: A geometric perspective." Concepts in Magnetic Resonance Part A: An Educational Journal 26.1 (2005): 1-10.

5. Shcherbakova, Yulia, et al. "PLANET: an ellipse fitting approach for simultaneous T1 and T2 mapping using phase‐cycled balanced steady‐state free precession." Magnetic resonance in medicine 79.2 (2018): 711-722.

6. Bıyık, Erdem, et al. "Factorized sensitivity estimation for artifact suppression in phase‐cycled bSSFP MRI." NMR in Biomedicine 33.4 (2020): e4228.

7. N. McKibben, G. Tarbox, M. A. Mendoza, and N. K. Bangerter, “Robust Coil Combination for bSSFP Elliptical Signal Model,” Proceedings of the 28th Annual Meeting of the ISMRM.

8. Shcherbakova, Yulia, et al. "On the accuracy and precision of PLANET for multiparametric MRI using phase‐cycled bSSFP imaging." Magnetic resonance in medicine 81.3 (2019): 1534-1552.

9. Gach, H. Michael, Costin Tanase, and Fernando Boada. "2D & 3D Shepp-Logan phantom standards for MRI." 2008 19th International Conference on Systems Engineering. IEEE, 2008.

10. Hoff MN, Xiang Q-S. “Correcting bSSFP Distortion near Metals with Geometric Solution Phase.” In: Proc. ISMRM, Salt Lake City, USA, 2013. p. 2563.

11. Taylor M, Valentine J, Whitaker S, Hoff MN, Bangerter N. “Field Mapping using bSSFP Elliptical Signal Model.” In: Proc. ISMRM, Hawaii, HI, USA, 2017. P. 3920.

Figures

TR-ellipses are approximately identical at FA>70°. (a) Simulated TR-ellipses at TR1/TR2=3/3.45ms, FA=3° and (b) FA=100°. (c) TR-ellipses sampled at 4 points (0°,90°,180°,270°) and geometric centers. Rotation is due to 1333Hz off-resonance. (d) TR-ellipses are rotated to superimposition, producing a virtual ellipse. Each phase-cycle is in a unique position on the ellipse. (e) Knowledge of the geometric center of one ellipse and 2 phase-cycles on the other allows rotation about the origin until superimposition. The angle the line rotates through is the equivalent off-resonance.

Simulated Shepp-Logan T1, T2 results using the original PLANET single TR-ellipse method as well as the proposed dual-TR virtual ellipses (SNR=73). T1/T2 values correspond to scalp, bone marrow, CSF, blood-clot, and gray and white matter (Ref ⁹). Performance is similar using single-TR ellipses and the proposed virtual ellipses at SNR~70. Low SNR (<60) experiments fail uniformly due to sensitivity in PLANET’s ellipse fitting dependence.

Representative simulated field maps using both 8 and 6 phase-cycles (SNR=73). The PLANET field maps required phase-unwrapping while the proposed methods did not. The proposed methods in each case outperform PLANET field maps. The PLANET residual image contains artifacts due to the streak-banding caused by the linear off-resonance which can be seen in the estimate. PLANET with 6 phase-cycles performs poorly even in good SNR conditions using single or multiple TR-ellipses. Proposed methods result in good field maps, improving by an order of magnitude in almost every case.

Normalized root mean square error (NRMSE) vs SNR for simulated tissues at FA=100°/10°. Quality of the virtual ellipses at FA=10° was unacceptable due to violation of the large FA assumption and are omitted from the plots. At high SNR, the standard PLANET algorithm yielded more accurate T1/T2 mapping, but the virtual ellipse performed better below SNR~85. PLANET’s off-resonance outperforms the virtual ellipse estimate at low FA and SNR values, but the virtual ellipse method outperforms when the high FA assumption holds.

Field map estimates from a cylindrical phantom. A modified TrueFISP pulse sequence with 200 dummy pulses ensured steady state. 8 linearly spaced phase-cycles between 0 and 2$$$\pi$$$ at TR=6ms and FA=70° were acquired for the single ellipse PLANET (left) while 4 linearly spaces phase-cycles were acquired for each of two TR-ellipses (TR1=6ms, TR2=12ms) (right). The PLANET field map estimate (left) suffers from phase wrapping and artifacts due to the high FA while the proposed multi-TR estimate only suffers from discontinuities due to the large difference between TR1 and TR2.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1830