Introduction

Quantitative MRI is an emerging tool in detection and monitoring of diseases [1]. However, it generally requires acquisition of multiple images, causing increased scan time compared to single-contrast imaging. Therefore, high resolution (HR) quantitative MRI is not achievable clinically, especially for 3D isotropic imaging. A common way to address this problem is using interpolation methods like bicubic interpolation [2] and k-space zero-padding [3]. Unfortunately, these interpolation methods generally introduce the blocking artifacts and blur the images [4]. Recent studies have developed the spatial super-resolution (SR) reconstruction techniques based on deep-learning network to improve the resolution of medical images [5]. However, these SR methods can NOT be directly applied to quantitative MRI due to the following reasons. Firstly, deep learning methods usually require a large amount of paired LR and HR MR images, which take quite a long time to obtain. Secondly, data normalization is an essential operation before deep neural network training, which can stable gradients to reduce the exploding gradient problem. However, in quantitative MRI, images with different contrasts have various minimum and maximum pixel values. Normalization would break the connections between corresponding pixels and leads to inaccurate fitting results. In this work, we designed an unsupervised shallow convolutional neural network, which needs no external training data and can directly obtain the high-resolution weighted images and the accurate quantitative map.

Methods

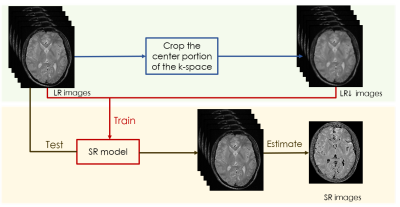
We concatenate weighted images as a whole to operate normalization. A state-of-the-art image-specific self-supervised SR convolution network called ZSSR [6], which leverages on the power of the patch recurrence across the scales of a single LR image was applied while incorporating this idea. The framework of our algorithm is shown in figure 1.Given a series of low-resolution weighted MR images $$$I_{LR}$$$ , the training data were extracted from the $$$I_{LR}$$$ itself. At training time, the LR input images $$$I_{LR\downarrow}$$$ are directly obtained by downscaling the $$$I_{LR}$$$, which select the central portion of k-space. Then, the LR-HR training pairs consist of this lower-resolution version of $$$I_{LR}$$$ and the $$$I_{LR}$$$ themselves. At testing time, we apply the trained SR model to $$$I_{LR}$$$, using the $$$I_{LR}$$$ as the LR input images to the network so that the desired HR outputs $$$I_{HR}$$$ are recovered. We also modified the loss function of our quantitative SR model. When dealt with natural images, the deep-learning SR method usually use the L1 loss as the loss function since it provides better convergence than the widely used L2 loss [5]: $$$L_{pixel_{l1}}(\hat{I},I) = \frac{1}{hwc}\sum_{i,j,k}\mid\hat{I}_{i,j,k}-I_{i,j,k}\mid$$$.Where h, w and c are the height, width and number of channels of the evaluated images, respectively. However, since the pixel loss doesn’t take the quality of the estimated map into account, the results often lack precision. Therefore, the loss function was modified as the following formation:$$$L_{map_{l1}}(\hat{I},I) = \frac{1}{hwc}\sum_{i,j,k}\mid map(\hat{I}_{i,j,k})-map(I_{i,j,k}) \mid $$$,$$$LOSS = \alpha L_{pixel_{l1}} + \beta L_{map_{l1}}$$$. The models are evaluated on a series of brain $$$T_{1\rho}$$$-weighted MR images with an in-plane resolution of 240 x 216 acquired on a 3T United-imaging scanner from 2 subjects at five different TSLs: 1, 10, 20, 40, 60. These images are regarded as ground-truth, which was down-sampled by selecting the central portion of k-space to simulate an LR counterpart by a factor of 2.

Results

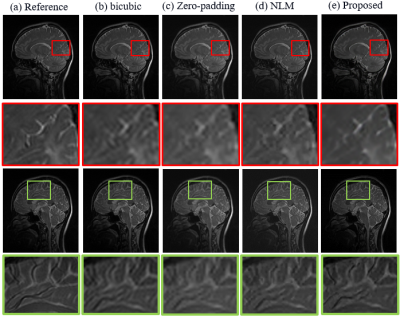
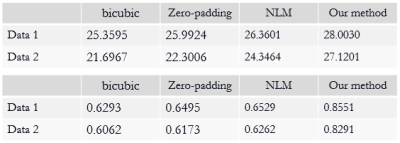
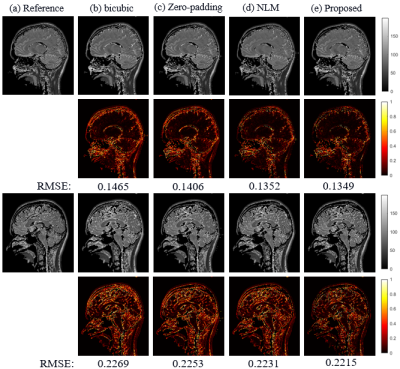
The SR results of $$$T_{1\rho}$$$-weighted images and estimated map with bicubic interpolation、zero-padding and non-local means (NLM) [7], which is also an approach that take advantage of image self-similarity, are shown in figure 2. Visually, the proposed approach can significantly improve resolution, especially the edges were sharpened compared to other methods. Table 1 demonstrates the comparison of the PSNR and SSIM measurements calculated between reference images and the SR results. The proposed method outperforms all other three comparison approaches statistically. Figure 3 shows the SR results of quantitative map with all four methods.The difference maps and RMSE measurements are also presented respectively. Overall the RMSE value is also smaller for the map calculated with the proposed method than with the other three approaches.

Discussion and conclusion

The proposed approach can recover the HR weighted images as well as the accurate quantitative map precisely without any external paired training data. The results of our method compared with other approaches are also visually appealing and have quantitative improvements. As a preprocessing step, the proposed technique also potentially benefits the following MR image analysis task like segmentation.

Acknowledgements

This work is supported in part by the National Natural Science Foundation of China under grant nos.61771463,81971611, National Key R&D Program of China nos.2020YFA0712202,2017YFC0108802,the Innovation and Technology Commission of the government of Hong Kong SAR under grant no.MRP/001/18X, and the Chinese Academy of Sciences program under grant no.2020GZL006.