Introduction

MRI is a non-invasive imaging modality that gives excellent soft-tissue contrast. Several acceleration methods have been introduced to overcome the slow nature of MRI acquisition, thus improving patient comfort and reducing costs. Deep learning algorithms offer improved reconstruction quality and high computational efficiency, compared to classical compressed sensing algorithms. Most of the current methods learn the parameters of the network from a large dataset of fully-sampled and noise-free images. Unfortunately, fully sampled and noise-free training data is not available or difficult to be acquired in several MR applications, such as high-resolution MRI.

In this work, we propose an ensemble SURE (ENSURE) loss for the end-to-end training of image reconstruction algorithms only using undersampled k space data. We first show that a weighted loss metric obtained from an ensemble of images, each acquired with a different sampling pattern, is an unbiased estimate for the MSE. We illustrate the proposed approach in the special cases of single-channel and multichannel MRI. The preliminary experiments demonstrate that the proposed ENSURE approach can give comparable results to supervised training in both direct-inversion and model-based settings while improving upon [5].

Proposed Method

We consider the case where an image $$$\boldsymbol{\rho}$$$ is only known through its measurements $$$\boldsymbol{y_s}$$$ from the acquisition operator $$$\mathcal A_{\boldsymbol s}$$$ parameterized by the random vector $$$\boldsymbol s$$$. The vector $$$\boldsymbol s$$$ can be viewed as the k-space sampling mask. The forward model to acquire noisy and undersampled measurements $$$\boldsymbol{y_s}$$$ is given by $$$\boldsymbol y_s = \mathcal A_{\boldsymbol s}~\boldsymbol{\rho} + \boldsymbol{n} $$$. Deep learning methods reconstruct fully sampled image $$$\boldsymbol{\widehat \rho}$$$ using a deep neural network $$$f_\Phi$$$ with trainable parameters $$$\Phi$$$ as $$$\widehat{\boldsymbol \rho} = f_{\Phi}(\boldsymbol {y_s})$$$.

Stein's Unbiased Risk Estimator (SURE methods have been extended to inverse problems in [1] with rank deficient $$$\mathcal A_{\boldsymbol s}$$$ operators, where the original $$${\rm MSE}$$$ is approximated by the projected MSE as $${\rm MSE}_{\boldsymbol s} = \mathbb E_{ \widehat{\boldsymbol \rho}} \left\| \mathbf P_{\boldsymbol s}\left(\widehat{\boldsymbol \rho} - \boldsymbol \rho\right)\right\|^2,$$Here $$$\mathbf P_s$$$ represents projection onto range space of $$$\mathcal A_{\boldsymbol s}^H$$$. However, in applications involving heavily undersampled measurements, $$$ {\rm MSE}_s$$$ is a poor approximation of $$${\rm MSE}$$$. To overcome the poor approximation of the $$$\rm MSE$$$ by $$$\rm MSE_{\boldsymbol s}$$$, we consider the sampling of each image by a different operator. In the MRI context, we assume the k-space sampling mask $$$\boldsymbol s$$$ to be a random vector drawn from the distribution $$$S$$$. Note that this acquisition scheme is realistic and can be implemented in many applications. Instead of the projected MSE, we consider the expectation of the projected MSE, computed over different sampling patterns and images. We derive the following ENsemble SURE (ENSURE) loss function, which does not require the fully sampled original image $$$\boldsymbol \rho$$$.

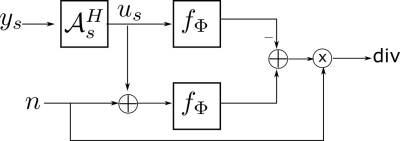
$$\mathcal L = \underbrace{\mathbb E_{\boldsymbol{u_s}} \left [\mathbb{E}_{\boldsymbol s}\left[ \|\mathbf{ W_s}\left(f_\Phi(\boldsymbol{u_s})- \boldsymbol{u_s} \right)\|_2^2\right]\right]} _{\mathrm{data~ term}} + \underbrace{2 \mathbb E_{\boldsymbol{u_s}} \left [\nabla_{\boldsymbol{u_s}} \cdot f_\Phi(\boldsymbol{u_s}) \right ]}_{\mathrm{divergence}}$$

Here $$$\mathbf u_s$$$ is the regridding reconstruction, $$$\mathbf W_s$$$ is the weighting of the k-space samples depending on the sampling distribution. The network divergence is estimated using Monte-Carlo SURE [2]. The detailed derivation of the proposed ENSURE approach is in [3]. Fig. 1 and 2 shows the implementation details of data-term and divergence term, respectively.

Experiments and Results

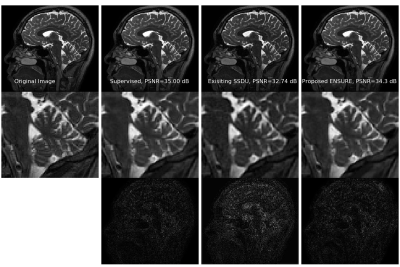
We consider a parallel MRI brain data obtained using a 3-D T2 CUBE sequence with Cartesian readouts using a 12-channel head coil at the University of Iowa on a 3T GE MR750w scanner. The matrix dimensions were $$$256\times232\times 208$$$ with a 1 mm isotropic resolution. Fully sampled multi-channel brain images of nine volunteers were collected, out of which data from five subjects were used for training. In contrast, the data from two subjects were used for testing and the remaining two for validation.

In Fig. 3, we compare the proposed ENSURE approach with a supervised learning approach named MoDL [4] and a recent unsupervised learning approach named SSDU [5]. We used an unrolling based architecture for all three approaches with three unrolls and shared weights. All three approaches used a standard 18-layer ResNet architecture with 3x3 filters and 64 feature maps at each layer. For SSDU, we used 60% of measured k-space for the data consistency step and 40% for MSE estimation, as suggested in [5]. The real and imaginary components of complex data were used as channels in all the experiments.

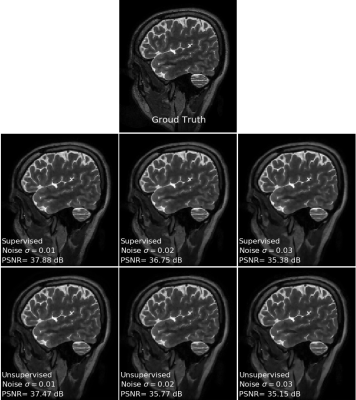
Figure 4 shows a comparison of the supervised and unsupervised learning at different noise levels while keeping all other experimental setups identical. It can be observed that unsupervised learning using the proposed ENSURE approach can give comparable performance to that of supervised training using MSE.

Acknowledgements

This work is supported by 1R01EB019961-01A1. This work was conducted on an MRI instrument funded by 1S10OD025025-01.