1773

Noise2Recon: A Semi-Supervised Framework for Joint MRI Reconstruction and Denoising using Limited Data

Arjun D Desai^1,2, Batu M Ozturkler¹, Christopher M Sandino³, Brian A Hargreaves^2,3,4, John M Pauly^3,5, and Akshay S Chaudhari^2,5,6
¹Electrical Engineering (Equal Contribution), Stanford University, Stanford, CA, United States, ²Radiology, Stanford University, Stanford, CA, United States, ³Electrical Engineering, Stanford University, Stanford, CA, United States, ⁴Bioengineering, Stanford University, Stanford, CA, United States, ⁵Equal Contribution, Stanford University, Stanford, CA, United States, ⁶Biomedical Data Science, Stanford University, Stanford, CA, United States

Synopsis

Deep learning (DL) has shown promise for faster, high quality accelerated MRI reconstruction. However, standard supervised DL methods depend on extensive amounts of fully-sampled, ground-truth data and are sensitive to out-of-distribution (OOD), particularly low-SNR, data. In this work, we propose a semi-supervised, consistency-based framework (termed Noise2Recon) for joint MR reconstruction and denoising that uses a limited number of fully-sampled references. Results demonstrate that even with minimal ground-truth data, Noise2Recon can use unsupervised, undersampled data to 1) achieve high performance on in-distribution (noise-free) scans and 2) improve generalizability to noisy, OOD scans compared to both standard and augmentation-based supervised methods.

Introduction

Accelerated MRI can alleviate the high cost and slow speed of MR imaging. Current reconstruction methods rely on parallel imaging (PI) and compressed sensing (CS), but these methods have limited acceleration or require long reconstruction times^1–3. Recent deep learning (DL) approaches may enable further accelerations compared to PI and CS^4–6. However, standard supervised DL algorithms require vast amounts of fully-sampled references, which are difficult to collect prospectively at scale⁷. Additionally, the sensitivity of these algorithms to out-of-distribution (OOD) data, particularly low-SNR acquisitions, limit their generalizability⁸. Though supervised training on noise-augmented images is feasible, its impact on reconstructing both in-distribution (high-SNR) and OOD (low-SNR) data has not been investigated.

While fully-sampled datasets are scarce, undersampled, noisy scans may be more accessible, leading to an opportunity to use both fully-sampled and undersampled scans in a semi-supervised DL approach. In this study, we propose Noise2Recon– a semi-supervised, consistency-based framework for joint MR reconstruction and denoising that uses a limited number of fully-sampled references. We evaluate whether Noise2Recon improves reconstruction performance and generalizability to noisy data in data-limited settings.

Theory

Noise2Recon uses denoising regularization to reduce overfitting to the image reconstruction task when supervised examples are limited. Unlike supervised algorithms, where only scans with fully-sampled references (supervised) are used during training, Noise2Recon training is complemented by a noise augmentation-consistency training paradigm (schematic-Fig.1). Examples without fully-sampled references (unsupervised) are augmented with noise, and the Noise2Recon model ($$$f_{\theta}$$$) generates reconstructions for both unsupervised images $$$x^{(u)}$$$ and noise-augmented undersampled images $$$x^{(u)} + \epsilon$$$. To encourage denoising during the reconstruction process, a consistency L1-loss is enforced between the two reconstructions (Eq.1), where $$$A$$$ is the imaging model and $$$i$$$ indexes the different coils. Here, noise is modeled as the complex-valued, masked noise: $$$\epsilon=UF\mathcal{N}(0,\sigma)$$$, where $$$U$$$ is the undersampling mask, $$$F$$$ is the Fourier operator, and $$$\mathcal{N}$$$ is a zero-mean complex-gaussian distribution with standard deviation σ. The total loss is the weighted sum of the supervised loss ($$$L_{sup}$$$) and the consistency loss ($$$L_{cons}$$$).
$$\min_{\theta}\sum_i|f_{\theta}(x_i^{(u)},A_i)-f_{\theta}(x_i^{(u)}+\epsilon,A_i)|\;\;\;\;(1)$$

Methods

19 fully-sampled 3D fast-spin-echo knee scans (http://mridata.org) were partitioned into 14, 2, and 3 subjects (4480, 640, and 960 slices) for training, validation, and testing. 2D image reconstruction was performed for slices reformatted in the ky-kz direction. Data was undersampled using Poisson Disc undersampling with a 20x20 calibration region to estimate sensitivity maps using the JSENSE technique⁹. For each testing scan, a unique undersampling trajectory was generated using a reproducible random seed.

To simulate reference-scarce settings, fully-sampled references were excluded for a random subset of training scans. For the training set $$$\mathcal{T}$$$, $$$\mathcal{T}_k\subset\mathcal{T}$$$ is the set of $$$k$$$ training scans for which fully-sampled references were retained. Scans not in $$$\mathcal{T}_k$$$ ($$$x\in\mathcal{T}\setminus\mathcal{T}_k$$$) were retrospectively undersampled with fixed masks to simulate unsupervised training scans. Experiments were performed at 12x and 16x acceleration factors for $$$k$$$=1,2,3,5,10 scans, where $$$\mathcal{T}_1\subset\mathcal{T}_2\dots\subset\mathcal{T}_{10}$$$.

To evaluate performance on noisy (OOD) test scans, fixed noise maps were generated at varying scan-magnitude-normalized standard deviations ($$$\sigma$$$=0.2,0.4,0.6,0.8,1.0) for each testing volume. During inference, these maps were added to the undersampled data following the noise model described above.

We compared Noise2Recon to two baselines: supervised training (Supervised) and supervised training with noise augmentations (Supervised+Aug). All DL networks used an unrolled architecture with eight residual blocks using the L1-loss^10,11. Supervised baselines were only trained on examples with fully-sampled references ($$$x\in\mathcal{T}_k$$$). Noise standard deviation for Noise2Recon and Supervised+Aug was selected uniformly at random from a predefined range: $$$\sigma\in[0.2,1.0]$$$. Supervised+Aug augmentations were applied with a probability p=0.2 based on hyperparameter tuning. Image quality was measured using normalized root-mean-squared error (nRMSE), structural similarity (SSIM), and peak-signal-to-noise ratio (pSNR).

Results

With only one supervised scan ($$$k$$$=1), Noise2Recon had similar nRMSE and pSNR (Fig.2) on in-distribution scans compared to fully-trained ($$$k$$$=14) Supervised models, with example images shown in Fig.3. Supervised+Aug models consistently underperformed both Noise2Recon and Supervised baseline.

Noise2Recon and Supervised+Aug models outperformed Supervised models on noisy scans (Fig.4). Unlike Supervised+Aug, Noise2Recon maintained high SSIM at varying noise levels with limited training data and recovered >95% of performance of the fully-trained Supervised+Aug model for all metrics (Fig.4). In noisy settings, Noise2Recon trained on a single acceleration generalized better to different accelerations (Fig.5).

Discussion

Noise2Recon achieved superior performance compared to both supervised baselines with limited data, particularly on noisy data. It also matched fully-supervised performance with almost 3x fewer examples. These results suggest that Noise2Recon may enable DL reconstruction with limited fully-sampled datasets and also provide a framework for using undersampled datasets during DL reconstruction.

Expectedly, incorporating noise during training increased robustness for reconstructing noisy scans. However, standard noise augmentations on supervised scans (Supervised+Aug) were minimally effective with limited supervised data and degraded performance on in-distribution, high-SNR data. In contrast, Noise2Recon generalized well to varying extents of noise and accelerations even with limited data, while maintaining high performance on in-distribution data. This generalizability may enable low-SNR acquisitions (reduced NEX, increased resolution and readout bandwidth, lower field strengths, etc.) without compromising reconstruction fidelity. Simulating OOD data for consistency regularization beyond noise may also be beneficial to generalizing to other artifacts.

Conclusion

We presented Noise2Recon– a semi-supervised, consistency-based reconstruction and denoising method capable of achieving high performance on low-SNR, OOD examples without compromising performance on in-distribution data with limited supervised data.

Acknowledgements

Research support provided by NSF 1656518, NIH AR077604, Precision Health and Integrated Diagnostics Center at Stanford, GE Healthcare, and Philips

References

1. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med. 1999;42(5):952-962. doi:10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S

2. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195. doi:10.1002/mrm.21391

3. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA). Magn Reson Med. 2002;47(6):1202-1210. doi:10.1002/mrm.10171

4. Zbontar J, Knoll F, Sriram A, et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI. 2018:1-29. http://arxiv.org/abs/1811.08839.

5. Chaudhari AS, Sandino CM, Cole EK, et al. Prospective Deployment of Deep Learning in MRI : A Framework for Important Considerations, Challenges, and Recommendations for Best Practices. J Magn Reson Imaging. August 2020:jmri.27331. doi:10.1002/jmri.27331

6. Sandino CM, Lai P, Vasanawala SS, Cheng JY. Accelerating cardiac cine MRI using a deep learning‐based ESPIRiT reconstruction. Magn Reson Med. 2021;85(1):152-167. doi:10.1002/mrm.28420

7. Cole EK, Pauly JM, Vasanawala SS, Ong F. Unsupervised MRI Reconstruction with Generative Adversarial Networks. arXiv. August 2020. http://arxiv.org/abs/2008.13065. Accessed December 12, 2020.

8. Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK. Assessment of the generalization of learned image reconstruction and the potential for transfer learning. Magn Reson Med. 2019;81(1):116-128. doi:10.1002/mrm.27355

9. Ying L, Sheng J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE). Magn Reson Med. 2007;57(6):1196-1202. doi:10.1002/mrm.21245

10. Diamond S, Sitzmann V, Heide Gordon Wetzstein F. Unrolled Optimization with Deep Priors.; 2018.

11. Sandino CM, Cheng JY, Chen F, Mardani M, Pauly JM, Vasanawala SS. Compressed Sensing: From Research to Clinical Practice with Deep Neural Networks: Shortening Scan Times for Magnetic Resonance Imaging. IEEE Signal Process Mag. 2020;37(1):117-127. doi:10.1109/MSP.2019.2950433

Figures

Fig. 1: Noise2Recon complements supervised training (blue pathway) with unsupervised training (red pathway) by enforcing network consistency between reconstructions of both unsupervised data and their noise-augmented counterparts. Unsupervised data is augmented by a noise map ε=U*F*N(0,σ), where σ is selected uniformly at random and the undersampling operator U is determined from the undersampled k-space. Scans with fully-sampled references follow the supervised training paradigm. The total loss is the weighted sum of the supervised (L_sup) and consistency (L_cons) losses.

Fig. 2: Noise2Recon outperformed both supervised training methods with and without noise augmentations when number of supervised scans (k) were limited at multiple acceleration factors (top-12x, bottom-16x). Naïve noise augmentations in supervised training (orange) can lead to unstable performance in reconstructing in-distribution, low-noise scans, but this is mitigated with Noise2Recon. Noise2Recon also converged faster to, and in some cases exceeded performance of, supervised training on the full training dataset of 14 subjects (gray dashed line).

Fig. 3: Sample reconstructions at 12x acceleration (top) and 2x errors (bottom) using zero-filled SENSE method, supervised model, supervised model with noise augmentations, and Noise2Recon. Supervised baselines were trained using the full supervised dataset (k=14) while Noise2Recon was trained using one supervised scan (k=1). Noise2Recon recovered fine structures, such as the medial collateral ligament (red arrow), and had similar image quality metrics to both supervised baselines.

Fig. 4: Reconstruction performance for 12x (top) and 16x (bottom) undersampled scans corrupted at varying noise levels (σ). Supervised models were trained with one (solid) or fourteen (dashed) supervised scans. Noise2Recon outperformed both 1-subject supervised methods at all noise levels. Noise2Recon achieved similar nRMSE and pSNR as noise-augmented supervised training but outperformed the latter in SSIM. Noise2Recon image quality metrics had low sensitivity to increasing σ and acceleration, which may indicate higher reconstruction robustness in noisy settings.

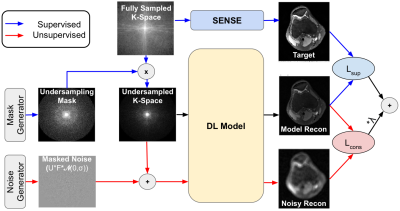
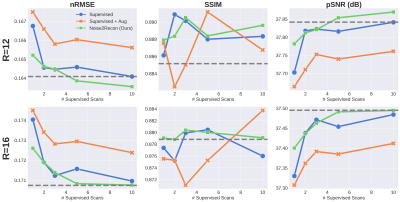
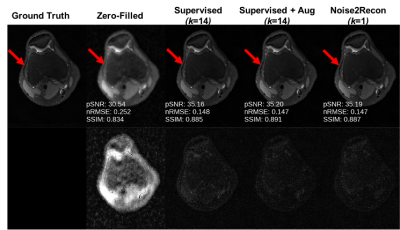
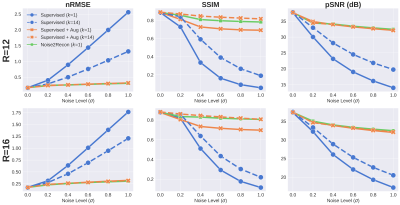
Fig. 5: Generalizing to reconstruction at multiple acceleration factors (R) at noise level σ=1 when trained on 16x undersampled images. k indicates number of supervised training scans. Noise2Recon outperforms Supervised+Aug with 7% of supervised data and reduces variance seen with supervised methods in the low-data regime. Additionally, Supervised+Aug baselines do not exhibit any performance recovery at lower acceleration factors (R=8,12). Noise2Recon improved performance in these cases without considerably compromising performance at higher accelerations (R=20,24).

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1773