1768

Extending Scan-specific Artifact Reduction in K-space (SPARK) to Advanced Encoding and Reconstruction Schemes

Yamin Arefeen¹, Onur Beker², Heng Yu³, Elfar Adalsteinsson^4,5,6, and Berkin Bilgic^5,7,8
¹Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, ²Department of Computer and Communication Sciences, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, ³Department of Automation, Tsinghua University, Beijing, China, ⁴Massachusetts Institute of Technology, Cambridge, MA, United States, ⁵Harvard-MIT Health Sciences and Technology, Cambridge, MA, United States, ⁶Institute for Medical Engineering and Science, Cambridge, MA, United States, ⁷Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, ⁸Department of Radiology, Harvard Medical School, Boston, MA, United States

Synopsis

Scan-specific learning techniques improve accelerated MRI reconstruction by training models using data solely from the specific scan; but they are constrained to Cartesian imaging and require an integrated auto-calibration signal (ACS), reducing acceleration. This abstract extends the scan-specific model SPARK, which estimates and corrects reconstruction errors in k-space, to arbitrary acquisitions and reconstructions. We demonstrate improvements in 3D volumetric imaging either with an integrated or external ACS region and in simultaneous multi-slice, wave-encoded imaging. SPARK enables an order of magnitude acceleration with ~2-fold reduction in reconstruction error compared to advanced reconstruction techniques that serve as its input.

Introduction

Standard machine learning techniques for MRI reconstruction¹ can struggle with a lack of available training data and generalization across imaging scenarios.² Scan-specific models avoid these issues by improving accelerated MRI reconstruction using data solely from the specific scan.^3-6

These techniques work remarkably well, but can be constrained to Cartesian imaging and require a large auto-calibration signal (ACS) where the middle portion of k-space is fully sampled, reducing total acceleration. We extend our scan specific model, SPARK,⁷ which estimates and corrects reconstruction errors in k-space, so that it flexibly applies to arbitrary acquisition and reconstruction schemes. We show that SPARK enables an order of magnitude acceleration with ~2-fold reduction in reconstruction error in 3D imaging using integrated ACS or an external reference scan and in simultaneous-multi-slice (SMS) wave-encoded imaging.⁸

Methods and Experiments

SPARK Framework

Let $$$y_{est}$$$ be the k-space estimate after an initial reconstruction from acquired data $$$y_{acq}$$$. We train a model to estimate the k-space correction term for the $$$c^{th}$$$ coil:
$$θ^* = argmin_θ||CropACS[y_{acq}^c - y_{est}^c - f_θ^c(y_{est})||_2$$
such that $$$f_{θ^*}^c$$$ estimates the reconstruction error in the ACS of the $$$c^{th}$$$ coil using $$$y_{est}$$$ as input. Then, we correct the reconstructed k-space of the $$$c^{th}$$$ coil:
$$y_{corrected}^c = y_{est}^c + f_{θ^*}^c(y_{est})$$
We repeat for all coils and assume that learning residuals in the ACS region will generalize to estimating errors outside of the ACS region, much like the assumed generalization of GRAPPA kernels trained with ACS.

3D Volumetric SPARK with an Integrated ACS Region

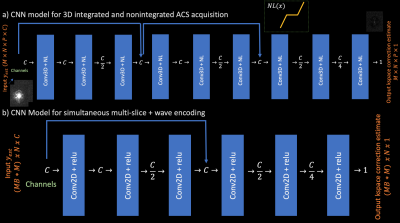
Scan-specific networks require large ACS regions; here we take advantage of increased ACS size in 3D-imaging. We reconstruct $$$y_{est}$$$ with un-regularized 3D GRAPPA⁹ and train the 3D convolutional-neural-network (CNN) shown in Figure 1a on an integrated 3D-ACS region to learn a 3D k-space correction term. Applying this custom nonlinearity improved upon biased results from normal relu by allowing negative activations:¹⁰
$$NL(x) = x + ReLU(\frac{x-1}{2}) + ReLU(-\frac{x+1}{2})$$
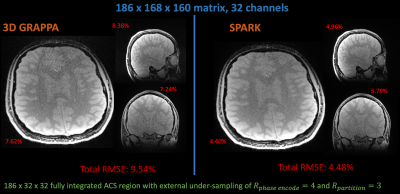
Figure 2 compares un-regularized 3D GRAPPA with 3 × 3 kernels to SPARK reconstructions on a 1.3 × 1.1 × 1 mm voxels, 244 × 185 × 160 m field-of-view, 32-channel, TR/TE = 25/4 ms Cartesian GRE acquisition retrospectively undersampled by a factor of 4 x 3 with an integrated 186 x 32 x 32 ACS region.

3D Volumetric SPARK Without an Integrated ACS Region

It can be more efficient to exclude integrated ACS during contrast encoding, and instead utilize a minimum TE/TR GRE scan for calibration. To apply SPARK in this regime, we propose a hybrid sampling scheme where the ACS region is undersampled at a lower rate than the rest of k-space. The reference scan can be used to reconstruct the undersampled ACS region, and then SPARK can be applied.

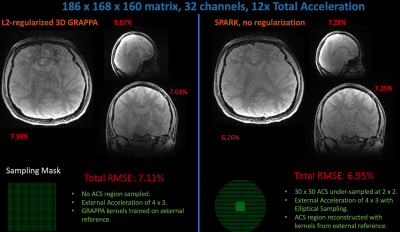
Figure 3 compares a 4 x 3 GRAPPA reconstruction with optimized l2-regularization and 3 x 3 kernels trained on a reference scan to a SPARK reconstruction with 2 x 2 undersampling in the 186 x 30 x 30 ACS region, 4 x 3 undersampling outside of the ACS region, and elliptical undersampling on the aforementioned GRE dataset. Note, the GRAPPA input to SPARK did not employ any regularization.

SPARK with Simultaneous multi-slice wave-encoded acquisitions

Let $$$A$$$ be the generalized-SENSE forward model that uses Fourier encoding, coil sensitivities and wave point spread functions to map multi-slice images to acquired sms-wave-encoded data, $$$y_{acq}$$$.¹¹ We can obtain an initial estimate for our images by solving
$$x_{est} = argmin_x||y_{acq} - A x||_2$$
Estimated k-space can be generated with $$$y_{est} = A x_{est}$$$, then SPARK can be applied, assuming an integrated ACS region exists in $$$y_{acq}$$$.

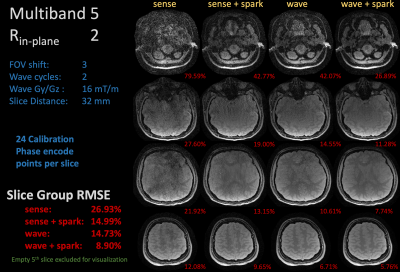
Figure 1b illustrates the CNN model used for the sms-wave acquisitions. Figure 4 compares baseline reconstruction schemes with SPARK on simulated multi-band 5, R_inplane = 2 measurements from the aforementioned dataset. We assume that each slice has an ACS region of 24 phase encoding lines.

In all experiments, data were acquired with a 32-channel receive coil.

Results

Code at: https://github.com/YaminArefeen/sparkIsmrm2021

Illustrated in Figure 2, SPARK achieves ~2x improvement in RMSE over the volume in a 3D acquisition with integrated ACS and slice-by-slice RMSE improvement.

In Figure 3, SPARK exploits the same reference scan used in 3D-GRAPPA to achieve improvement at the representative slices while matching GRAPPA’s acceleration. Further improvements can be expected if SPARK employs a regularized 3D-GRAPPA reconstruction as input.

Figure 4 compares sense (without wave-encoding), sense + SPARK, wave encoding, and wave + SPARK reconstructions on a simulated multiband 5, in-plane acceleration 2 acquisition. SPARK provides qualitative and quantitative rmse improvement for both the sense and wave reconstructions. Wave + SPARK achieves the best results on both the total slice group and individual slices.

Conclusions

We extend our scan-specific learning based technique, SPARK, beyond 2D-Cartesian imaging. SPARK improved reconstruction fidelity in 3D-imaging with and without an integrated ACS region and in SMS-wave encoded acquisitions. Although we show only three applications here, our SPARK framework can be applied flexibly to any acquisition and reconstruction scheme where the data can be described by a forward model.

Acknowledgements

This work was supported in part by research grants R01 EB017337 & R01 HD100009. In addition, this material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. 1122374. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation

References

1. Knoll F, Hammernik K, Zhang C, Moeller S, Pock T, Sodickson DK, et al. Deep-Learning Methods for Parallel Magnetic Resonance Imaging Reconstruction: A Survey of the Current Approaches, Trends, and Issues. IEEE Signal Process Mag. 2020;37: 128–140.

2. Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK. Assessment of the generalization of learned image reconstruction and the potential for transfer learning. Magn Reson Med. 2019;81: 116–128.

3. Akçakaya M, Moeller S, Weingärtner S, Uğurbil K. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magn Reson Med. 2019;81: 439–453.

4. Zhang C, Moeller S, Weingärtner S, Uğurbil K, Akçakaya M. Accelerated MRI using residual RAKI: Scan-specific learning of reconstruction artifacts. Annual Meeting of the International Society of Magnetic Resonance in Medicine. 2019. Available: https://par.nsf.gov/servlets/purl/10095914

5. Zhang C, Moeller S, Weingärtner S, Uğurbil K, Akçakaya M. Accelerated Simultaneous Multi-Slice MRI using Subject-Specific Convolutional Neural Networks. Conf Rec Asilomar Conf Signals Syst Comput. 2018;2018: 1636–1640.

6. Hosseini SAH, Moeller S, Weingärtner S, Uğurbil K, Akçakaya M. Accelerated Coronary Mri Using 3D Spirit-Raki With Sparsity Regularization. 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019). 2019. pp. 1692–1695.

7. Beker O, Liao C, Cho J, Zhang Z, Setsompop K, Bilgic B. Scan-specific, Parameter-free Artifact Reduction in K-space (SPARK). arXiv [eess.IV]. 2019. Available: http://arxiv.org/abs/1911.07219

8. Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, et al. Wave-CAIPI for highly accelerated 3D imaging. Magn Reson Med. 2015;73: 2152–2162.

9. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002;47: 1202–1210.

10. Singh NM, Iglesias JE, Adalsteinsson E, Dalca AV, Golland P. Joint Frequency and Image Space Learning for Fourier Imaging. arXiv [cs.CV]. 2020. Available: http://arxiv.org/abs/2007.01441

11. Gagoski BA, Bilgic B, Eichner C, Bhat H, Grant PE, Wald LL, et al. RARE/turbo spin echo imaging with simultaneous multislice Wave-CAIPI. Magn Reson Med. 2015;73: 929–938.

Figures

Figure 1: a) Trained model to estimate k-space correction terms for 3D acquisitions. b) Trained model to estimate the k-space correction term for the sms-wave encoded acquisition. We model sms through readout concatenation; thus the model uses readout concatenated k-space as input. 2D and 3D convolutions are 3 × 3 and 3 × 3 × 3 respectively and arrows represent skip connections. Both models take the reconstructed k-space across all coils as input and output the correction at a particular coil.

Figure 2: Comparisons between 3D GRAPPA and the associated 3D SPARK reconstruction for three representative slices using an integrated ACS region. The acquisition measured an integrated 32 × 32 ACS region and undersampled the phase encode and partition dimensions by a factor of 4 and 3 respectively. SPARK achieves a factor of 2 improvement in RMSE over the whole volume, and also achieves RMSE improvement on the axial, coronal, and sagittal slices shown.

Figure 3: Comparison between 4 x 3 accelerated, l2-regularized GRAPPA using 3D kernels trained on a reference scan, and an acceleration matched SPARK acquisition (un-regularized GRAPPA-input). SPARK measured the 30 x 30 undersampled ACS region with 2 x 2 undersampling and the exterior of kspace with 4 x 3 undersampling in the phase encode and partition directions. SPARK exploits the same reference scan used in GRAPPA to achieve improvement at the representative slices.

Figure 4: Comparisons between sense, sense + SPARK, wave encoding, and wave + SPARK reconstructions on a simulated multiband 5, in-plane acceleration 2, acquisition. Wave was simulated with a maximum Gy/Gz gradient amplitude of 16 $$$\frac{mT}{m}$$$ and two cycles. Complex gaussian noise was added to all simulated data. SPARK provides qualitative and quantitative rmse improvement for both the sense and wave reconstructions. Wave + SPARK achieves the best results on both the total slice group and individual slices.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

1768