Introduction:

Quantitative susceptibility maps (QSMs), derived from phase and magnitude images of MRI-based susceptibility-weighted images (SWI), characterize pathological neuroanatomical features such as microbleeds, aberrant levels of iron, calcium, and myelin. Artifacts like motion and Gibbs-ringing [1] can obscure tissue boundaries caused during reconstruction that excludes high spatial frequencies on the edges of the k-space, also known as truncation, results in artifacts that usually appear as rings around high-contrast tissue boundaries of the image. The artifact is due to the reconstruction of the finite k–space using an inverse 2D Fourier transformation where the high spatial frequencies have been eliminated. High frequencies are on the edges of the k-space, and low frequencies at the center of the k-space are results of the strong gradients and the low gradients, respectively. However, in MR imaging we are limited by sampling in the finite k-space, and excluding the high-frequency signals leads to a truncation effect and commonly, Gibbs overshooting. These artifacts usually appear as a ringing effect near high-contrast tissue boundaries in the image. There are methods that reduce this effect in the spatial reconstructed images. One recent method implemented in MRtrix3 (mrdegibbs) uses a local subvoxel shift [2]. Deep learning-based methods show promising results, but they currently exist only for T1-weighted images. Here we introduce a U-Net based 3-dimensional deep learning network to remove Gibbs artifacts from SWI-derived QSM.

Methods:

SWI were obtained from the UK Biobank (UKB) resource[3], collected on a 3T Siemens Skyra scanners (32-channel receiver head coil; 3D axial acquisition, double-echo GRE, TE = 9.42, 20 ms, 0.8x0.8x3 mm3, FOV = 256x288x48 mm3). Magnitude and phase images from the 32 coils were combined using the Bernstein method [4]. Individual brain masks were generated from the magnitude images using HD-BET [5]. For each mask, the phase image was spatially unwrapped through a fast phase unwrapping algorithm [6]. A local field map was generated through background removal using the Laplacian boundary value method [7]. Finally, QSMs were reconstructed using Morphology Enabled Dipole Inversion (MEDI) [8]. Figure 1 shows this preprocessing pipeline.
We visually quality controlled 11290 SWI scans and discarded all with visible Gibbs ringing for model building purposes. From images with minimal or no artifacts, we generated artificial Gibbs artifacts by removing high frequency elements from the Fourier space, causing inaccurate sampling of sharp edges after applying the inverse Fourier transform. We truncated ~50-90% of high frequency components in the k-space[9]: A QSM slice contains approximately 7300 high frequency elements after FFT. To simulate Gibbs, we removed 55%, 70%, 80%, or 90% of these elements from the masks. We used a combination of truncations on three mask sizes. High frequency elements at the edges of k-space correspond to sharp intensity differences at the boundaries of the mask, so removing them causes ringing in image space. Artifacts were added to every axial slice. For each volume, 12 new volumes containing simulated artifacts were generated with varied ringing intensities and widths.
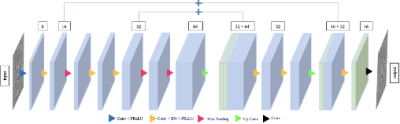
We implemented a 3D U-Net model [10], trained using the following parameters on 93% of the subject scans: Adam optimizer [11], batch size = 64, learning rate = 10-5. The volumes were split into training (80%) and test (20%) sets. Validation was performed on a left-out sample, the remaining 7% of the data. Our network architecture (Figure 2) consists of two pairs of encoder and decoder blocks. Each encoder has two convolution layers, each containing a PReLU activation function, a batch normalization layer, and a max pooling layer. The pre-processed and quality-controlled QSMs were cropped to 180x240x48 using “CenterCropOrPad” from Torchio [12] and then input to the encoder. Each decoder contains two deconvolution layers, followed by batch normalization and a max pooling layer with the final up-convolution layer.
We compared outputs of our UNet model to the Gibbs-free input and calculated the mean squared error across the full image for all Gibbs levels of our validation set. We also ran mrdegibbs and compared those outputs to the ground truth. MSE of both de-Gibbs methods were compared using a paired t-test.

Results:

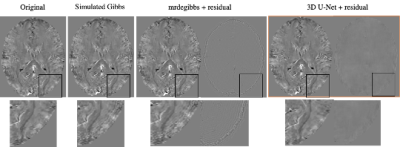
From 11290 SWI datasets, we noted 8903 had some artifacts (2229 major) and were excluded; 1966 had visually undetectable artifacts. These were augmented and used to generate ringing as described. 1846 were used for model generation, and 120 for validation. The average MSE from our U-Net model and mrdegibbs were 1.30*10^-5 and 3.25*10^-5, respectively. We found the difference was statistically significant at p < 6.1x10^-17, showing our model significantly reduced the Gibbs artifact compared to mrdegibbs. A visual representation of one image is shown in Figure 3.

Discussion:

We provide for the first time, a tool specifically designed to remove Gibbs ringing artifacts from QSM, which may outperform models intended for broad use across MR contrasts. Other methods may over-correct and remove anatomical features such as microbleeds and small vasculature, important features in QSM.

Conclusion:

Our model can quickly be run across Gibbs-artifact corrupted QSM maps and will allow for high-powered population studies of brain vasculature and tissue microstructure with SWI.

Acknowledgements

This research was conducted using the UK Biobank Resource under Application Number ‘11559’. This research was supported by the National Institutes of Health (NIH): R01 AG059874, P41 EB015922. NJ is MPI of a research related grant from Biogen Inc for image processing.