1762
AutoSON: Automated Sequence Optimization by joint training with a Neural network1Department of Electrical and computer Engineering, Seoul National University, Seoul, Korea, Republic of
Synopsis
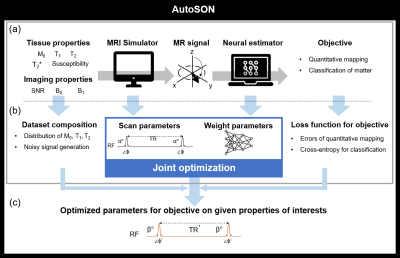
In MRI, scan parameters are carefully selected for desired results. We propose a new optimization method, AutoSON, that determines optimal scan parameters for flexibly-selected objectives on given tissue properties such as distribution and noises. AutoSON optimizes not only scan parameters but also a neural estimator, which extracts the desired information from MR signals (e.g., quantification mapping). The method successfully optimized the flip angles in DESPOT1 for T1 mapping and classification of white matter and gray matter. The last example does not have a simple analytic equation, and therefore, demonstrates a potential utility of the method.
Introduction
In MRI, scan parameters (e.g., TR, FA) are selected for a desired objective by considering properties of interests (e.g., T1, noises). Previously, a few optimization methods have been utilized to select the scan parameters1. However, these methods typically require assumptions such as an unbiased network based on noisy measurement, limiting their applications. Recently, deep-learning methods have been proposed to design MRI sequences2, 3, which focus on the development of new sequences, not optimizing sequence parameters of an existing sequence. In this study, we proposed a new automation method that jointly optimizes both sequence parameters and a neural network that extracts information for an objective (AutoSON). This new method allows flexible optimization to any objective (e.g. T1 mapping, classification of tissues) that can be modeled as a loss function in the network.Methods
[AutoSON]AutoSON jointly optimized scan parameters and a neural network (Fig. 1). The MR simulator generated signals corresponding to the scan parameters from a dataset that consists of tissue properties. The neural network utilized the simulated-signals as inputs in order to extract information of a desired objective (e.g., T1 mapping, tissue classification). The loss function of the neural network was back-propagated to the network parameters and sequence parameters, jointly optimizing the network and the sequence. The network structure was a multi-layer perceptron4. The training dataset was constructed for the objective (see Experiment 1-3).
[Experiment 1: T1 mapping using DESPOT1]
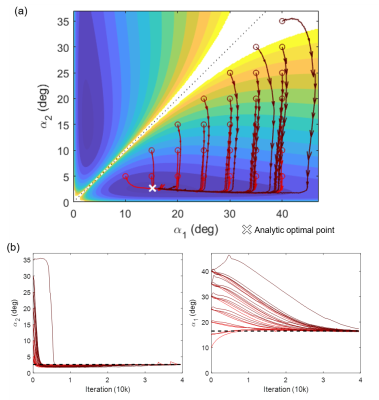
To verify the performance of AutoSON, we utilized DESPOT15, which has a simple analytic signal equation, as a test sequence to optimize scan parameters for T1 mapping6. In DESPOT1, two data with two FAs (α1, α2) are utilized. AutoSON optimized these two flip angles to provide high accuracy in T1 estimation for noise corrupted signals. The input for the network was magnitude signals from the DESPOT1 equation, and the output was a T1 value. Training signals are generated using the following parameters: T1=159 ms to 1695ms, T2=50ms, α1, α1=5°-40°, M0=0.5-1.0, TR/TE=10/5ms, and noise SD=2e-5. L2 loss was utilized. The optimization results were compared with the analytic solutions for T1=1645ms.
[Experiment 2: Tissue classification using DESPOT1]
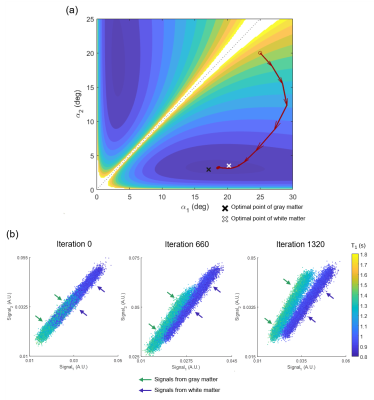
To demonstrate flexibility in optimization, the FAs for DESPOT1 were re-optimized to classify white matter and gray matter. The network input was the same but the output was modified to generate gray matter signal as 0 and white matter signal as 1. Two datasets, T1=1288±67ms and T2=76±5 ms for gray matter, and T1=917±32ms and T2=67±4ms for white matter, were generated with M0=0.5-1.0, noise SD=1e-3 and initial =25°,20°. The cross-entropy loss was utilized.
[Experiment3: T2 mapping using Partially spoiled SSFP]
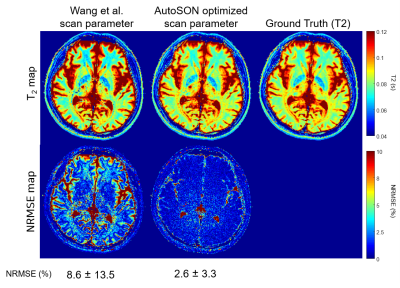
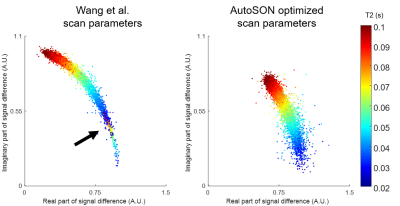
To demonstrate that AutoSON can optimize a sequence with no simple analytic form, we optimized phase-based T2 mapping7. This method uses two partially spoiled SSFP images with different RF phase increment. AutoSON optimized 3 parameters: FA, RF phase increment, and TR. The input of the network was the real and imaginary parts of the ratio of two complex signals. The output was a T2 value. For the training, the dataset was set to be results of M0, T1, and T2 of in-vivo data8. Large T2 (>200 ms; CSF) were excluded. The initial parameters were chosen from Wang et al. (FA=18°, phase increment=2°, TR=10ms). L2 loss was utilized. For MR signal simulator, a numerical simulation using Bloch equation was performed for 500 repetitions for steady-state. The 100 spins were induced a 2π phase dispersion in each repetition. Gaussian noises (SD:2e-4) were added to real and imaginary axes. Evaluation was performed for the scan parameters of AutoSON vs. Wang et al. by using the T2 mapping method from Wang et al. for a fair comparison of the sequence parameter optimization. The T2 mapping results of in-vivo data (another subject data from ref.8) were compared using normalized-root-mean-squared error (NRMSE).
Results
Figure 2 shows the optimization results of DESPOT1. When started with various initial points, all results converged to FAs of α1=2.6±0.0° and α2=16.5±0.2°. These results are close to the optimum FAs from the analytic equation (α1=2.6°, α2=15.1°). For the task of classifying gray and white matter, the results are illustrated in Figure 3. The optimized FAs (α1=3.2°, α2=18.6°) were located in-between the optimal angles of white matter (α1=3.5°, α2=20.2°) and gray matter (α1=3.0°, α2=17.1°), showing reasonable results. As the optimization progresses, the separation of the two signals becomes clear (Figure 3b). The T2 mapping results are summarized in Figure 4. The optimized scan parameters (FA=74.2°, phase increment=2.4°, TR=6.7ms) yielded reduced NRMSE than the original parameters (NRMSE from 8.6±13.5% to 2.6±3.3%). When the signals are plotted for the two scan parameters (original vs AutoSON), the newly optimized results show a signal separation depending on T2, demonstrating successful optimization (Figure 5).Discussion and Conclusion
In this work, a new sequence optimization method that jointly optimizes scan parameters and a neural network was proposed. Our results demonstrates feasibility and some of the results (e.g. T2 mapping) may not be feasible (FA too large). Still, the proposed method is flexible in its optimization target. The optimization is performed as long as the target can be formulated as a loss function. Additionally, the method does not require any assumptions (e.g. unbiased estimator) and analytic equation, and therefore flexible.Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2018R1A2B3008445).References
[1] Teixeira, R. P. A., Malik, S. J., & Hajnal, J. V. (2018). Joint system relaxometry (JSR) and Cramer‐Rao lower bound optimization of sequence parameters: a framework for enhanced precision of DESPOT T1 and T2 estimation. Magnetic resonance in medicine, 79(1), 234-245.
[2] Loktyushin, A., Herz, K., Dang, N., Glang, F., Deshmane, A., Doerfler, A., ... & Zaiss, M. (2020). MRzero--Fully automated invention of MRI sequences using supervised learning. arXiv preprint arXiv:2002.04265.
[3] Zhu, B., Liu, J. Z., Koonjoo, N., Rosen, B., & Rosen, M. (2018). AUTOmated pulse SEQuence generation (AUTOSEQ) using Bayesian reinforcement learning in an MRI physics simulation environment. In Proc. 26th Annu. Meeting ISMRM.
[4] Lee, J., Lee, D., Choi, J. Y., Shin, D., Shin, H.-G., & Lee, J. (2020). Artificial neural network for myelin water imaging. Magnetic Resonance in Medicine, 83(5), 1875-1883.
[5] Deoni, S. C., Rutt, B. K., & Peters, T. M. (2003). Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 49(3), 515-526.
[6] Schabel, M. C., & Morrell, G. R. (2008). Uncertainty in T1 mapping using the variable flip angle method with two flip angles. Physics in Medicine & Biology, 54(1), N1.
[7] Wang, X., Hernando, D., & Reeder, S. B. (2020). Phase‐based T2 mapping with gradient echo imaging. Magnetic Resonance in Medicine, 84(2), 609-619.
[8] Ji, S., Oh. S., Shin, H.-G., Lee, J., (2020). Quad-contrast imaging with quantitative relaxation maps for clinical neuro-evaluation, In Proc. 28th Annu. Meeting ISMRM.
Figures