Introduction

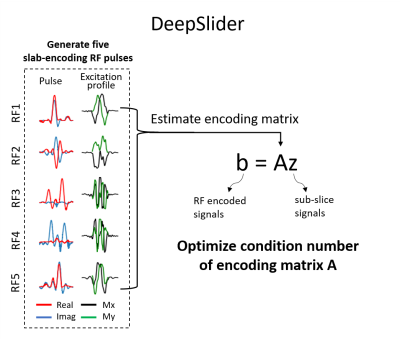
Acquiring a thin slice is important in high-resolution 2D neuroimaging. Recently, generalized slice dithered enhanced resolution (gSlider) was developed to generate high-resolution sub-slice images (e.g., 660 $$$μ$$$m diffusion MRI) via combinations of slab-encoding RF pulses^1,2. Recently, a deep reinforcement learning (DRL)-powered machine-designed RF pulse was proposed, providing a lower specific absorption rate (SAR) RF than conventional RF³. In this study, we utilize this DRL approach to generate an RF pulse set that has an improved condition number in the RF encoding matrix of gSlider, which determines the sensitivity of the design to noise (Fig. 1). The proposed method is referred to as DeepSlider. Additionally, we expand the dimension of DeepSlider reconstruction from real signal to complex signal, proposing another method, DeepSlider_complex, expanding application of the pulse to phase-based imaging.

Method

[Conventional gSlider] Conventional gSlider RF pulses are generated using publicly available codes⁴. Design parameters are as follows: TBWP = 12, pulse duration = 11 ms, and five RF encoding basis. The signals, $$$b$$$, obtained from multiple MRI scans with the slab-encoding RF pulses can be modeled as a linear system of an encoding matrix, $$$A$$$, which is determined by the RF pulses, and sub-slice signals, $$$z$$$ (i.e., $$$b = Az$$$). The sub-slice signals are estimated by the pseudo-inverse of the equation.

[DeepSlider] The objective of DeepSlider is to generate five slab-encoding RF pulses that have the lowest condition number for A in order to improve the robustness of the pseudo-inverse against noise. To generate RF pulses, DRL creates RF pulses that maximize a reward function (see below). Then, the DRL-generated RF pulses are grouped into five, further optimized by the gradient descent stage using a loss function (see below). The TBWP and pulse duration are the same as in the gSlider design.

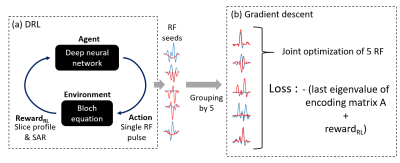
[DRL] DRL consists of a deep neural network agent and Bloch equation environment (Fig. 2a). The reward function is defined as follows:$$reward_{RL}={c_1}\sum_{z_p\in{Z_{pass}}}|M_{xy}(z_p)|-{c_2}\sum_{z_s\in{Z_{stop}}}|M_{xy}(z_s)|-c_3SAR$$where the first, second, and third terms represent passband magnetization, stopband magnetization, and SAR regularizer, respectively. The three coefficients, $$$c_1$$$ = 0.5, $$$c_2$$$ = 0.35, and $$$c_3$$$ = 10^-3, are determined empirically. In a single episode, the DRL agent generates an RF pulse as action. Then, the environment returns the reward of the RF pulse. Using this reward, the DRL agent updates the network weights with a proximal policy optimization algorithm. A total of 10⁵ RF pulses are generated.

[Gradient descent] In the gradient descent stage (Fig. 2b), 500 DRL-generated RF pulses, which have the highest rewards, are selected. Then, five RF pulses are randomly selected, resulting in 100 groups. The loss function of each group, which is minimized via the gradient descent, is defined as follows:$$loss=-eig_5(A)-\sum_{i=1}^5reward_{RL,i}$$where the first term $$$eig_5(A)$$$ is the fifth eigenvalue of the encoding matrix , and the second term is the sum of the reward function from DRL. Using this loss function, the RF pulses in each group are refined by gradient descent. After 2000 iterations, an RF pulse set with the minimum loss is chosen as the final result.

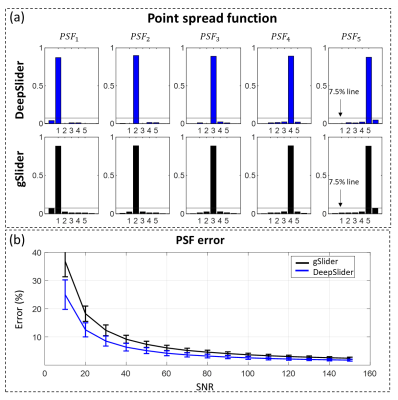
[Experiment] To evaluate the DeepSlider results, a point spread function (PSF) is calculated as follows: $$PSF_i=(A^TA+\lambda{I})^{-1}A^T\delta_i$$where $$$\delta_i$$$ is an impulse at the $$$i$$$th sub-slice, $$$\lambda$$$ is a Tikhonov regularizer (= 0.4) and $$$PSF_i$$$ is the impulse response of $$$\delta_i$$$. To explore the effects of noise, PSF errors of gSlider and DeepSlider are estimated by varying SNR from 10 to 150. Also, the mean SAR for the RF pulses and the condition number of the encoding matrix $$$A$$$ are compared.

[Complex DeepSlider] Since gSlider slab-encoding RF pulses are designed for the real part of a complex MRI signal¹, expanding it to complex is beneficial when the phase information is valuable. Hence, we design a new method, DeepSlider_complex, that allows the encoding matrix to be complex. To designed a complex encoding matrix A, the eigenvalue term in the loss function is modified by separating the real and imaginary parts of $$$A$$$ :
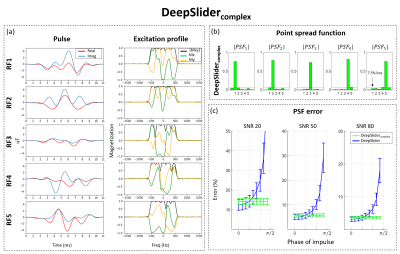
$$loss=-eig_5(real(A))-eig_5(imag(A))-\sum_{i=1}^5reward_{RL,i}$$To evaluate DeepSlider_complex results, the PSF errors of DeepSlider_complex and DeepSlider are estimated using sub-slice impulse, $$$\delta_i$$$ , which has a phase error from 0 to 80 for the SNR of 20, 50, and 80.

Results

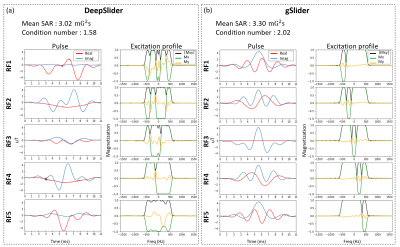
[DeepSlider] DeepSlider successfully reconstructs the sub-slice impulse functions (Fig. 3a), showing slightly lower SAR (= 3.02 (mG)²sec) and improved condition number (1.58) than those of gSlider (SAR: 3.30 (mG)²sec; condition number: 2.02). When the noise is added, DeepSlider shows lower PSF errors than those of gSlider, particularly at low SNRs (Fig. 3b).

[DeepSlider_Complex] DeepSlider_complex shows the potential of reconstructing robust sub-slice impulse functions (Fig. 5), producing the mean SAR of 3.11 (mG)²sec and condition number of 1.62 in real and 1.68 in imaginary. Compared to DeepSlider, DeepSlider_complex demonstrates slightly increased PSF errors due to the noise in the imaginary axis. However, the results report steady performances for the phase errors.

Discussion

In this study, the slab-encoding RF pules are designed using DRL and gradient descent. The results of DeepSlider show a lower condition number and a lower SAR, suggesting robustness to noise. Furthermore, DeepSlider_complex shows the potential of applying slab-encoding RF pulses for phase imaging or QSM.

Acknowledgements

We sincerely thank Professors Kawin Setsompop and William A Grissom for sharing their codes of the gSlider RF designing tool. This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2018R1A2B3008445), and funded by the MSIT (NRF-2018R1A4A1025891).