1758
A Deep-Learning Framework for Image Reconstruction of Undersampled and Motion-Corrupted k-space Data1Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, United States, 2Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States, 3Centre for Medical Image Computing, University College London, London, United Kingdom, 4A. A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 5Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 6Institute for Medical Engineering and Science, Massachusetts Institute of Technology, Cambridge, MA, United States
Synopsis
We propose a deep learning approach for reconstructing undersampled k-space data corrupted by motion. Our algorithm achieves high-quality reconstructions by employing a novel neural network architecture that captures the correlation structure jointly present in the frequency and image spaces. This method provides higher quality reconstructions than techniques employing solely frequency space or solely image space operations. We further characterize the motion severities for which the proposed method is successful. This analysis represents the first step toward fast image reconstruction in the presence of substantial motion, such as in pediatric or fetal imaging.
Introduction - Problem and Proposed Approach
Motion frequently corrupts MRI acquisitions, degrading image quality or necessitating re-acquisition1. The current strategies for mitigating these effects include: (1) navigators to detect if motion occurred and adjust acquisition of subsequent readouts, (2) undersampling, which reduces the acquisition time, and (3) retrospective motion correction. In this work, we develop a computational methodology where strategies (2) and (3) complement each other. Though separate techniques have been demonstrated for improving the quality and speed of motion-free undersampled reconstructions2-13 and for retrospective motion correction of fully-sampled data14-19, our strategy provides fast, high-quality correction of undersampling and motion artifacts present simultaneously.The proposed approach capitalizes on patterns in the correlation structure of MRI data in both k-space and image space (Fig. 1). Neural network architectures operating in both spaces correct artifacts native to k-space while also making image space refinements to produce coherent visual structures. Previously, we demonstrated such 'joint' networks in preliminary setups involving only motion or only undersampling20. Here, we demonstrate that joint neural networks are successful in a more realistic scenario where motion occurs in conjunction with an undersampled image acquisition.
The proposed framework accepts a wide range of imaging settings; here we consider a variable-density Cartesian undersampling scheme with preferential acquisition at the center lines of k-space. We assume a quasi-static motion model in which the object remains stationary during acquisition of any individual $$$k_y$$$-line but can move rigidly via rotations and translations between one $$$k_y$$$-line and the next. We defer modeling three-dimensional, through-slice motion effects for future work.
Methods
Network ArchitecturesWe investigate two novel neural network architectures that combine frequency and image space representations (Fig. 2). The 'Interleaved' architecture learns weighted linear combinations of frequency and image space features at each layer. The 'Alternating' architecture successively applies a frequency space convolution followed by an image space convolution at each layer. Each architecture contains ten consecutive copies of the appropriate joint layer.
Dataset
We demonstrate the proposed method on a large collection of T1-weighted brain MRI images from patients aged 55-90 in the Alzheimer's Disease Neuroimaging Initiative (ADNI)21. We include the mid-axial 2D 256x256 slice of each volume in the dataset. We split the dataset into 4,115 training images, 2,061 validation images, and 96 test images such that no subjects are shared between sets. We tune hyperparameters of the networks on the validation set and use the test set for the final evaluation once network training is completed.
Combined Undersampling and Motion Simulation
Fig. 3 illustrates the data-generation process used to simulate rigid motion. For each slice, we sample the fraction of lines $$$\gamma_{m}$$$ at which motion occurs. For each motion-affected line $$$L_i$$$, we sample three parameters of motion: $$$\Delta x_i$$$, $$$\Delta y_i$$$, $$$\Delta \theta_i$$$, corresponding respectively to a horizontal translation, vertical translation, and counterclockwise rotation about the slice origin. We synthesize the moved images $$$I^M_i$$$ by applying the sampled motion to the original image slice $$$I^O$$$. We simulate the corresponding k-space data $$$F^M_i$$$ and $$$F^O$$$ by applying a 2D Fourier transform to $$$I^M_i$$$ and $$$I^O$$$ respectively. We intersperse the appropriate sections of $$$F^O$$$ and all $$$F^M_i$$$ to simulate motion-corrupted k-space data. We then sample the full center 8% of $$$k_y$$$-lines and sample the remainder of k-space from a uniform distribution to achieve an overall 4x acceleration factor, producing the corrupted k-space data $$$F^C$$$. After simulating motion and undersampling, we normalize each input and output training pair by dividing by the maximum intensity in the corrupted image. The networks are trained to predict an estimate $$$\hat{I^O}$$$ of the original image $$$I^O$$$ from the undersampled motion-corrupted k-space data $$$F^C$$$. $$$I^O$$$ is the image corresponding to the subject position during acquisition of the center $$$k_y$$$-line.
Implementation Details
We train the networks until convergence using the Adam optimizer (learning rate 0.001) and a batch size of 4. The networks take an average of 1-2 days to train and 200 milliseconds to run on a single image on an NVIDIA RTX 2080Ti GPU.
Results and Discussion
We compare the proposed architectures to single-space baseline networks composed solely of frequency space convolutions or image space convolutions, with layer and feature numbers chosen to match the joint models. These single-space networks capture the salient characteristics of pure image-based or frequency-based deep learning approaches for undersampled image reconstruction2-13 and motion-correction14-19. Our experiments reveal that the joint architectures outperform the single-space baselines at all levels of motion corruption and qualitatively yield sharper reconstructions (Fig. 3). The quality of image reconstruction is more sensitive to the fraction of lines at which motion occurs than to other characteristics of the induced motion (Fig. 4). Qualitatively, the sharpness of individual image features degrades as motion occurs at an increasing fraction of lines. Visual assessment suggests that the joint networks produce high quality reconstructions for examples where motion is present at less than 3% of lines.Conclusions
We demonstrate an approach for reconstructing motion-corrupted, undersampled images and characterize the motion severities for which this method succeeds. Future work will extend this framework to multi-coil 3D volumetric data and non-rigid motion, with an ultimate application to correcting severe, unpredictable motion as in pediatric or fetal imaging.Acknowledgements
This research was supported by NIBIB, NICHD, NIA, and NINDS of the National Institutes of Health under award numbers 5T32EB1680, P41EB015902, R01EB017337, R01HD100009, 1R01AG064027-01A1, 1RF1MH123195-01 and 5R01NS105820-02, European Research Council Starting Grant 677697, project “BUNGEE-TOOLS”, Alzheimer's Research UK Interdisciplinary Grant ARUK-IRG2019A-003, and an NSF Graduate Fellowship.References
1. Andre, J. B. et al. Toward Quantifying the Prevalence, Severity, and Cost Associated With Patient Motion During Clinical MR Examinations. J. Am. Coll. Radiol. 12, 689–695 (2015).
2. Aggarwal, H. K., Mani, M. P. & Jacob, M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans. Med. Imaging 38, 394–405 (2019).
3. Akçakaya, M., Moeller, S., Weingärtner, S. & Uğurbil, K. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magnetic Resonance in Medicine vol. 81 439–453 (2019).
4. Cheng, J. Y., Mardani, M., Alley, M. T., Pauly, J. M. & Vasanawala, S. S. DeepSPIRiT: generalized parallel imaging using deep convolutional neural networks. In Annual Meeting of the International Society of Magnetic Resonance in Medicine (2018).
5. Hammernik, K. et al. Learning a variational network for reconstruction of accelerated MRI data. Magn. Reson. Med. 79, 3055–3071 (2018).
6. Han, Y., Sunwoo, L. & Ye, J. C. k -Space Deep Learning for Accelerated MRI. IEEE Trans. Med. Imaging 39, 377–386 (2020).
7. Hyun, C. M., Kim, H. P., Lee, S. M., Lee, S. & Seo, J. K. Deep learning for undersampled MRI reconstruction. Phys. Med. Biol. 63, 135007 (2018).
8. Lee, D., Yoo, J. & Ye, J. C. Deep residual learning for compressed sensing MRI. in 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017) 15–18 (2017).
9. Putzky, P. & Welling, M. Invert to Learn to Invert. in Advances in Neural Information Processing Systems (eds. Wallach, H. et al.) vol. 32 446–456 (Curran Associates, Inc., 2019).
10. Quan, T. M., Nguyen-Duc, T. & Jeong, W.-K. Compressed Sensing MRI Reconstruction Using a Generative Adversarial Network With a Cyclic Loss. IEEE Trans. Med. Imaging 37, 1488–1497 (2018).
11. Schlemper, J., Caballero, J., Hajnal, J. V., Price, A. N. & Rueckert, D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans. Med. Imaging 37, 491–503 (2018).
12. Yang, Y., Sun, J., Li, H. & Xu, Z. Deep ADMM-Net for Compressive Sensing MRI. in Advances in Neural Information Processing Systems (eds. Lee, D., Sugiyama, M., Luxburg, U., Guyon, I. & Garnett, R.) vol. 29 10–18 (Curran Associates, Inc., 2016).
13. Yang, G. et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Trans. Med. Imaging 37, 1310–1321 (2018).
14. Duffy, B. A. et al. Retrospective correction of motion artifact affected structural MRI images using deep learning of simulated motion. (2018).
15. Haskell, M. W. et al. Network Accelerated Motion Estimation and Reduction (NAMER): Convolutional neural network guided retrospective motion correction using a separable motion model. Magn. Reson. Med. 82, 1452–1461 (2019).
16. Johnson, P. & Drangova, M. Conditional generative adversarial network for three-dimensional rigid-body motion correction in MRI. in (2019).
17. Küstner, T. et al. Retrospective correction of motion-affected MR images using deep learning frameworks. Magn. Reson. Med. 82, 1527–1540 (2019).
18. Oksuz, I. et al. Detection and Correction of Cardiac MRI Motion Artefacts During Reconstruction from k-space. in Medical Image Computing and Computer Assisted Intervention – MICCAI 2019 695–703 (Springer International Publishing, 2019).
19. Usman, M., Latif, S., Asim, M., Lee, B.-D. & Qadir, J. Retrospective Motion Correction in Multishot MRI using Generative Adversarial Network. Sci. Rep. 10, 4786 (2020).
20. Singh, N. M., Iglesias, J. E., Adalsteinsson, E., Dalca, A. V. & Golland, P. Joint Frequency- and Image-Space Learning for Fourier Imaging. arXiv [cs.CV] (2020).
21. Mueller, S. G. et al. Ways toward an early diagnosis in Alzheimer’s disease: The Alzheimer’s Disease Neuroimaging Initiative (ADNI). Alzheimer’s & Dementia vol. 1 55–66 (2005).
Figures
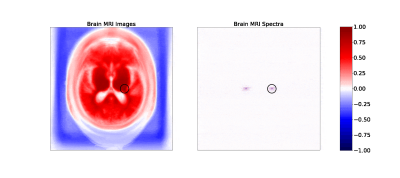
Figure 1. Maps of correlation coefficients between a single pixel (circled) and all other pixels in image (left) and frequency (right) space representations of the brain MRI dataset (click to view an animation of correlation patterns at several pixels). Both maps show strong local correlations useful for inferring missing or corrupted data. Frequency space correlations also display conjugate symmetry characteristic of Fourier transforms of real images.
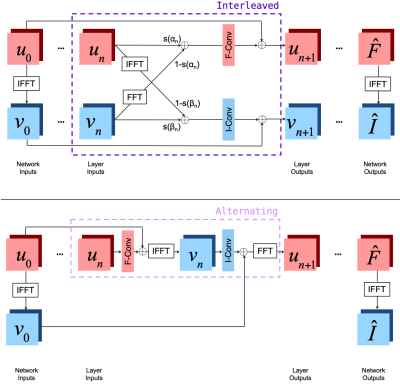
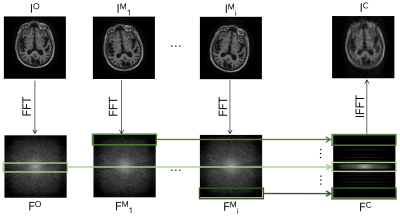
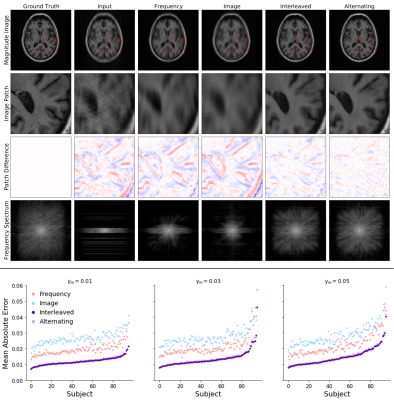
Figure 4. Top: Example reconstructions with motion induced at 3% of scanning lines. The Interleaved and Alternating architectures more accurately eliminate the 'shadow' of the moved brain and the induced ringing and blurring compared to the single-space networks.
Bottom: Comparison of all four network architectures on test samples with motion at varying fractions of lines. For nearly every example, the joint architectures (Interleaved and Alternating) outperform the single-space baselines.
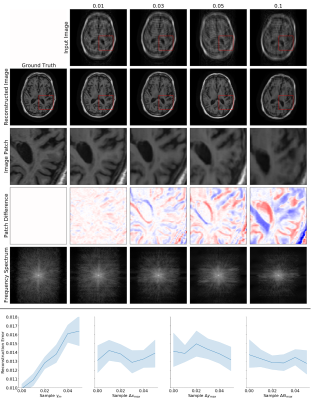
Figure 5. Top: Example Interleaved network reconstructions with motion at varying fractions of lines (columns). Reconstruction quality degrades as motion is present in more k-space lines.
Bottom: Reconstruction error as a function of motion parameters, with 95% confidence intervals. The largest motion parameters within a slice are reported as fractions of their maximum possible value (e.g., image width is the maximum possible horizontal translation). Reconstruction quality is more directly affected by the fraction of lines with motion than by translation or rotation size.